ggplot(mtcars, aes(x = wt, y = mpg)) +
geom_point() +
geom_smooth(method = "lm")`geom_smooth()` using formula = 'y ~ x'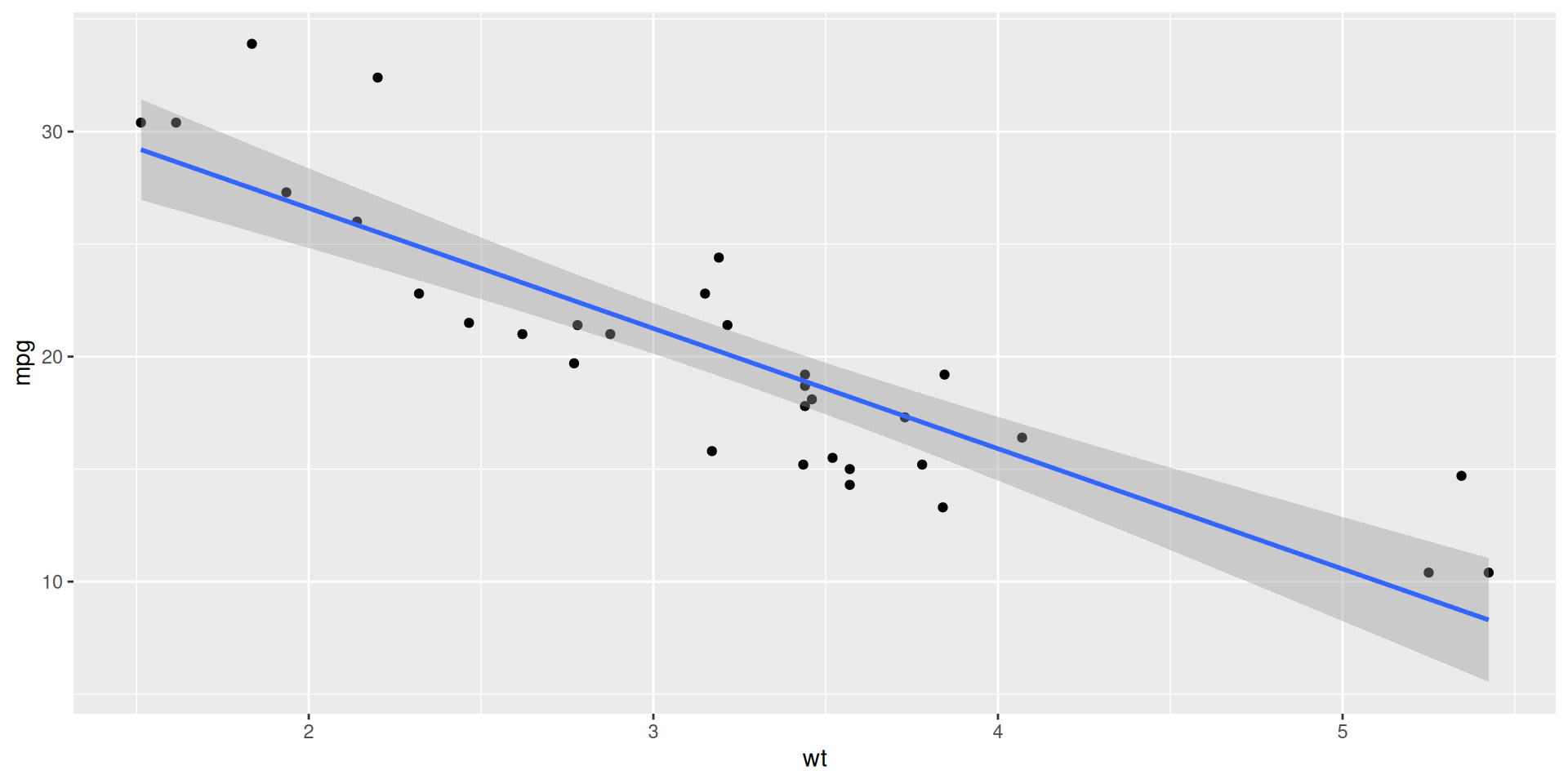
Final Thoughts: Statistical inference
Lecture 23
Recap: statistical inference
Point estimation: what’s your best guess?
Point estimation: what’s your best guess?
linear_reg() |>
fit(mpg ~ wt, data = mtcars) |>
tidy()# A tibble: 2 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) 37.3 1.88 19.9 8.24e-19
2 wt -5.34 0.559 -9.56 1.29e-10Sampling variability
Different data >> Different estimate. But how different?
Reassuring: recompute your estimate on other data and get basically the same answer. Sampling variation is low. Uncertainty is low. Results are more reliable;
Concerning: recompute your estimate on new data and get a wildly different answer. Sampling variation is high. Uncertainty is high. Results are less reliable.
How do we operationalize this?
The bootstrap
Construct different, alternative datasets by sampling with replacement from your original data. Each bootstrap sample gives you a different estimate, and you can see how vigorously they wiggle around:
Interval estimation
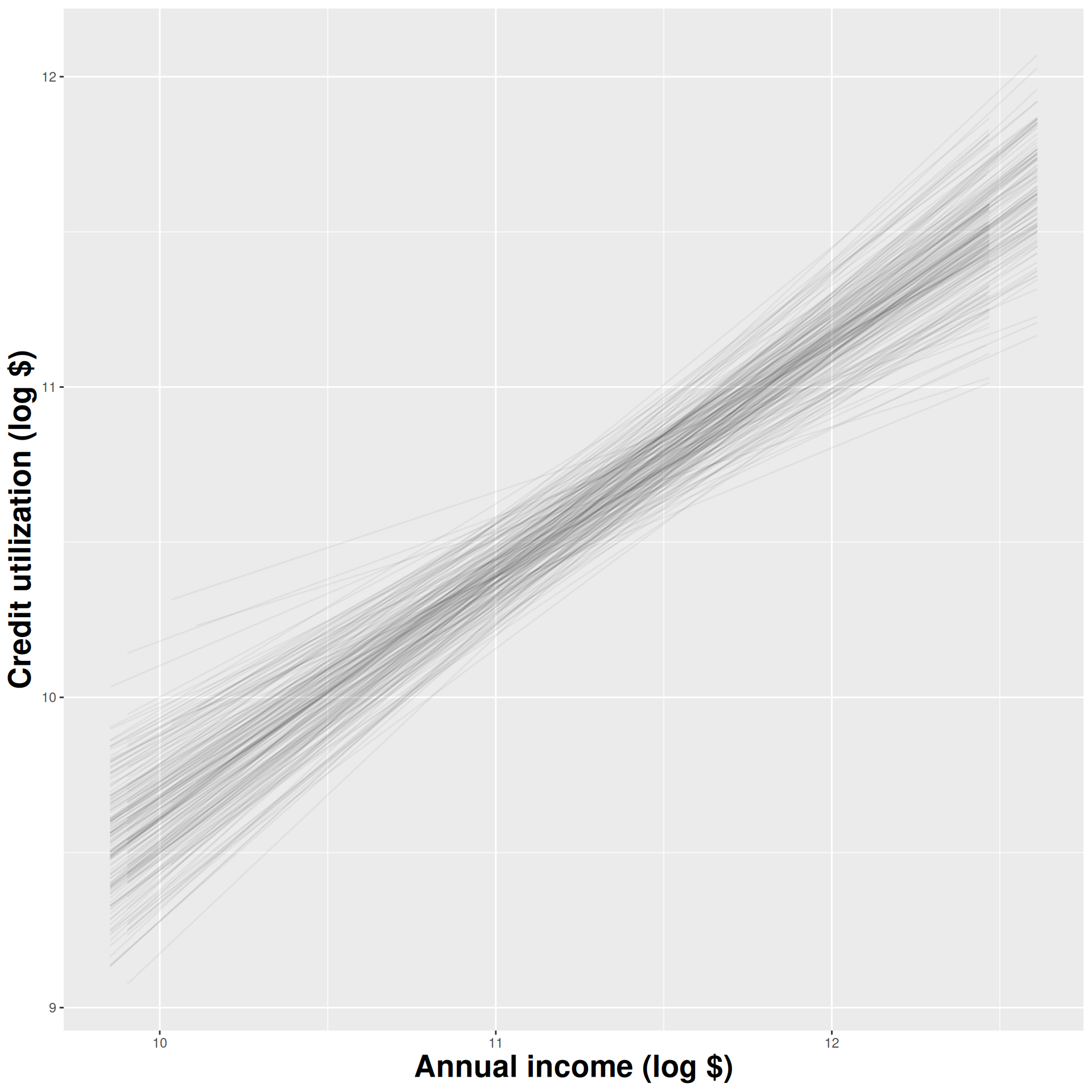
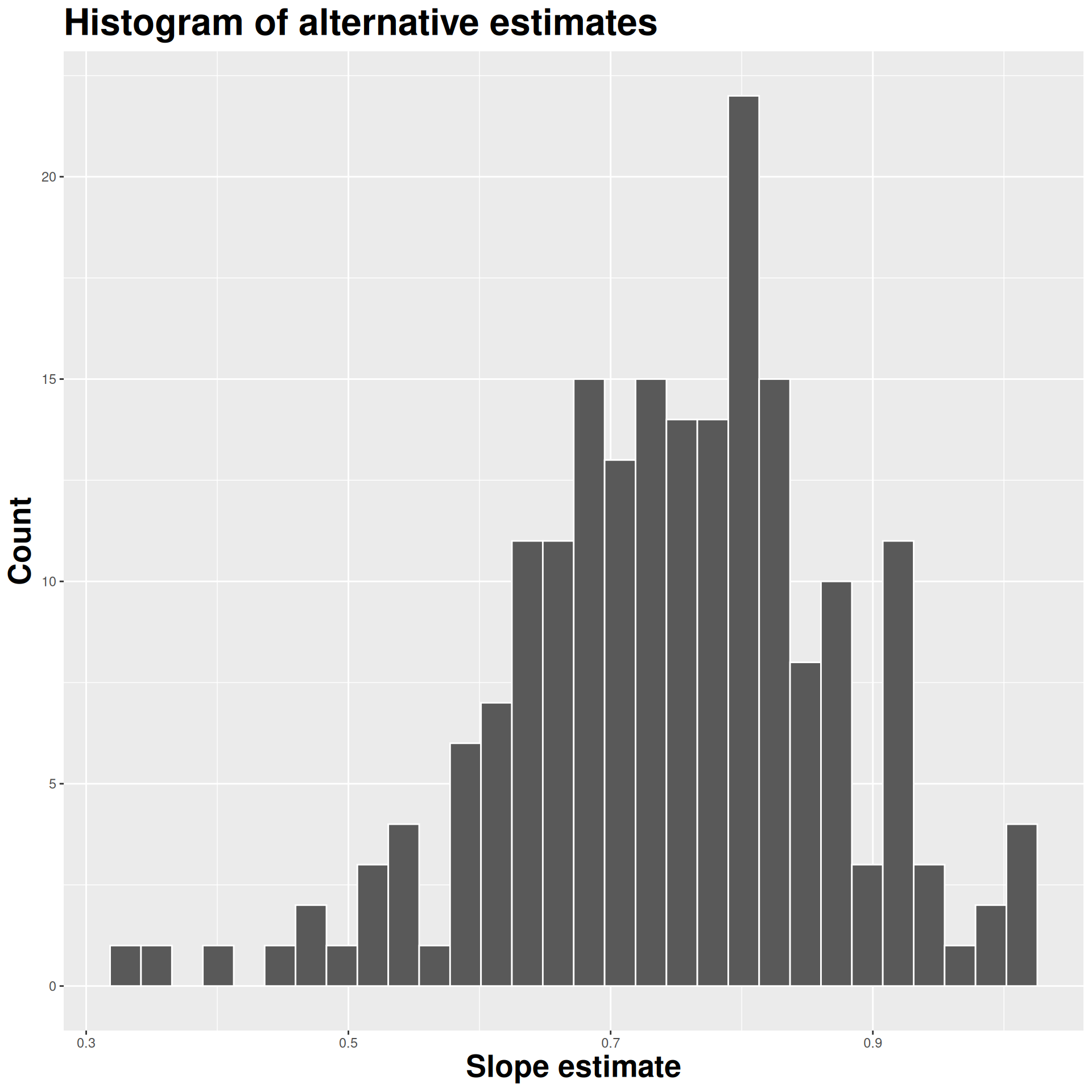
Use the bootstrap distribution to construct a range of likely values for the unknown parameter:
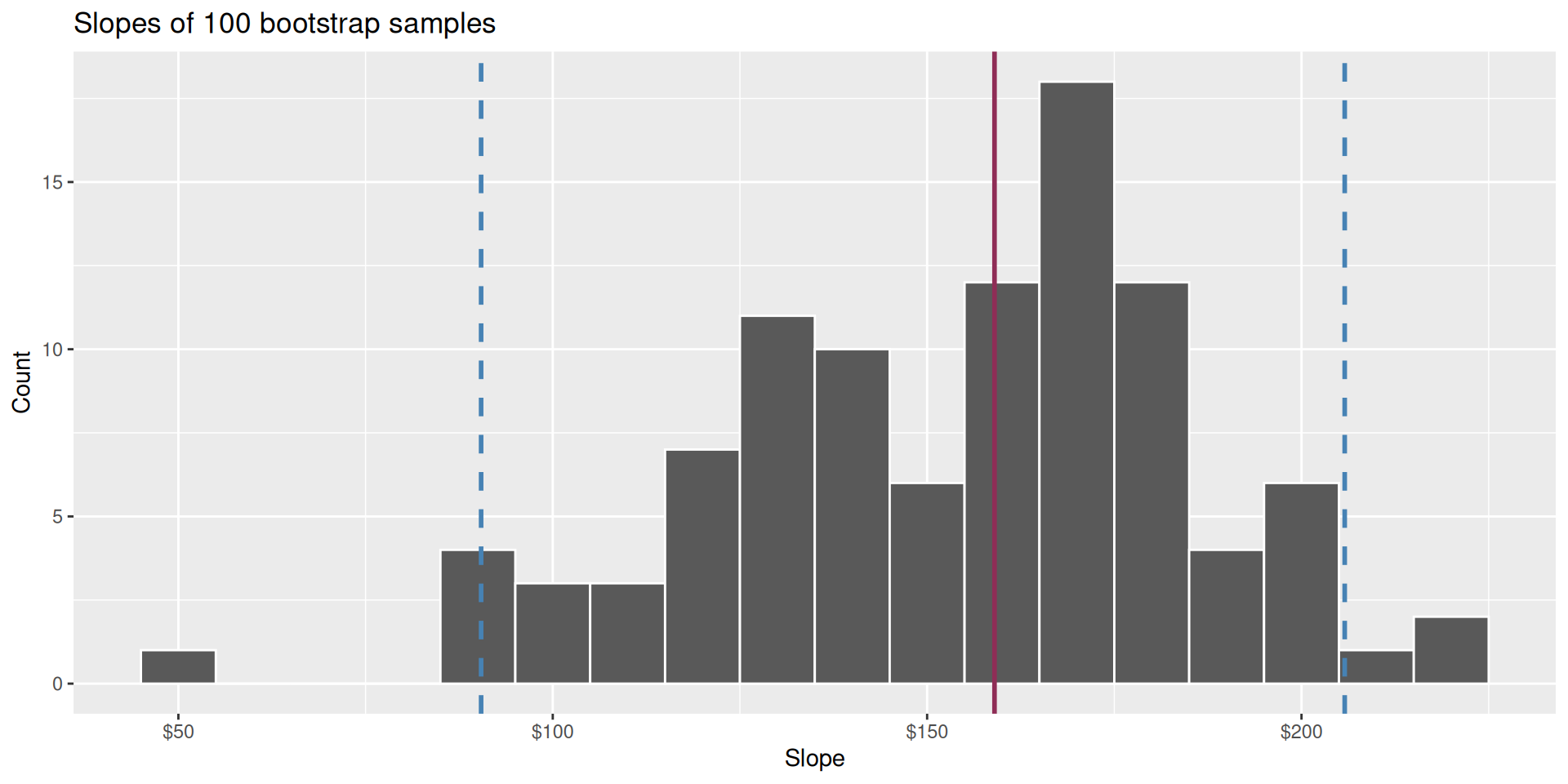
We use quantiles (think IQR), but there are other ways.
Hypothesis testing
Two competing claims about \(\beta_1\): \[ \begin{aligned} H_0&: \beta_1=0\quad(\text{nothing going on})\\ H_A&: \beta_1\neq0\quad(\text{something going on}) \end{aligned} \]
Do the data strongly favor one or the other?
How can we quantify this? p-values!
p-value
p-value is the fraction of the histogram area shaded red:
Discernibility level
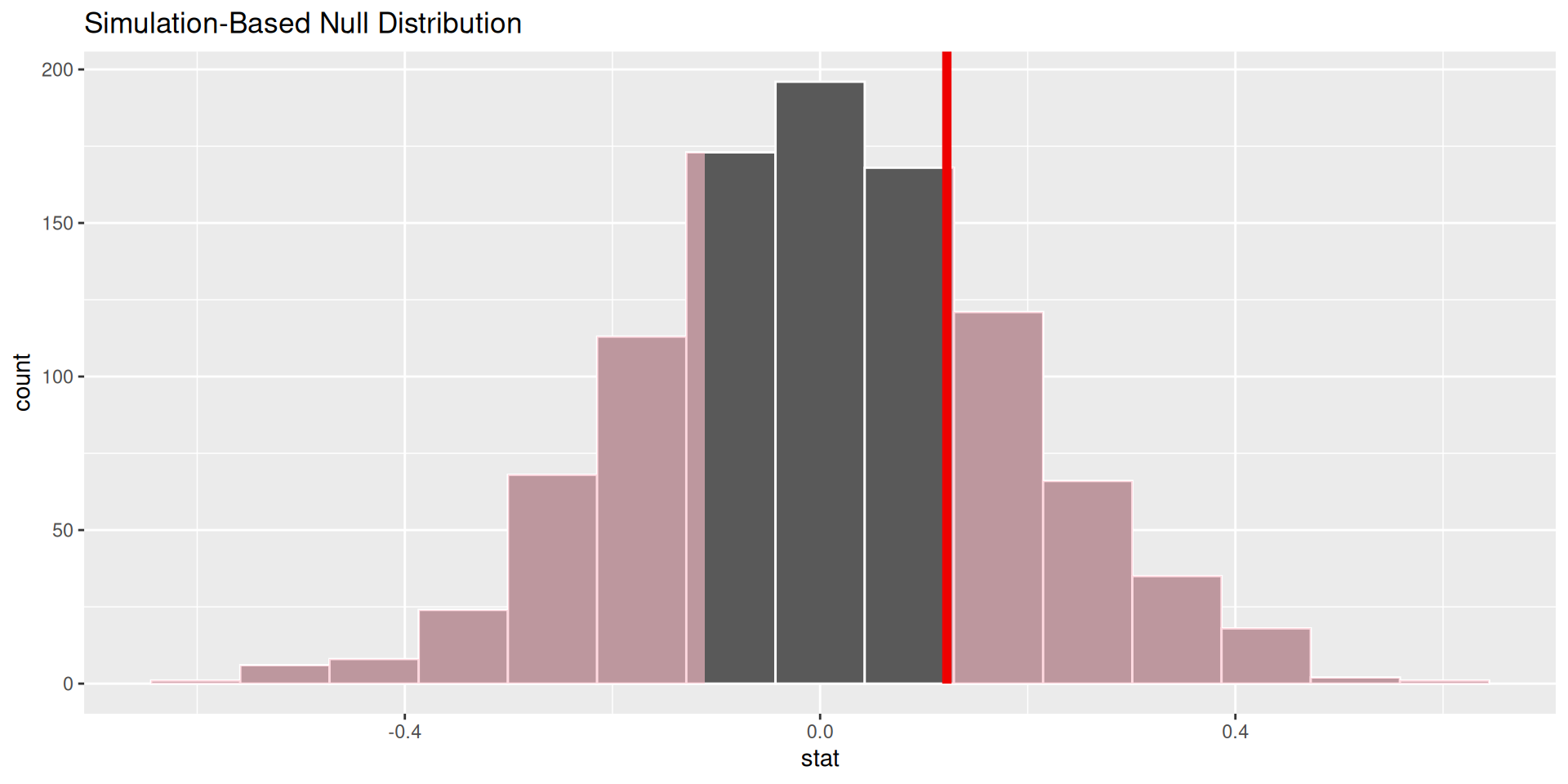
How do we decide if the p-value is big enough or small enough?
-
Pick a threshold \(\alpha\in[0,\,1]\) called the discernibility level:
- If \(p\text{-value} < \alpha\), reject null and accept alternative;
- If \(p\text{-value} \geq \alpha\), fail to reject null;
Standard choices: \(\alpha=0.01, 0.05, 0.1, 0.15\).
AE 17 Recap
Goal: Predicting mean household income using the percent of a county that is uninsured
We did inference with
counties_sample, a small sample of 25 counties in the US
Point Estimate
observed_fit <- counties_sample |>
specify(mean_household_income ~ uninsured) |>
fit()
observed_fit# A tibble: 2 × 2
term estimate
<chr> <dbl>
1 intercept 79489.
2 uninsured -884.Generating the null distribution
null_dist <- counties_sample |>
specify(mean_household_income ~ uninsured) |>
hypothesize(null = "independence") |>
generate(reps = 1000, type = "permute") |>
fit()
null_dist |>
filter(term == "uninsured") |>
ggplot(aes(x = estimate)) +
geom_histogram()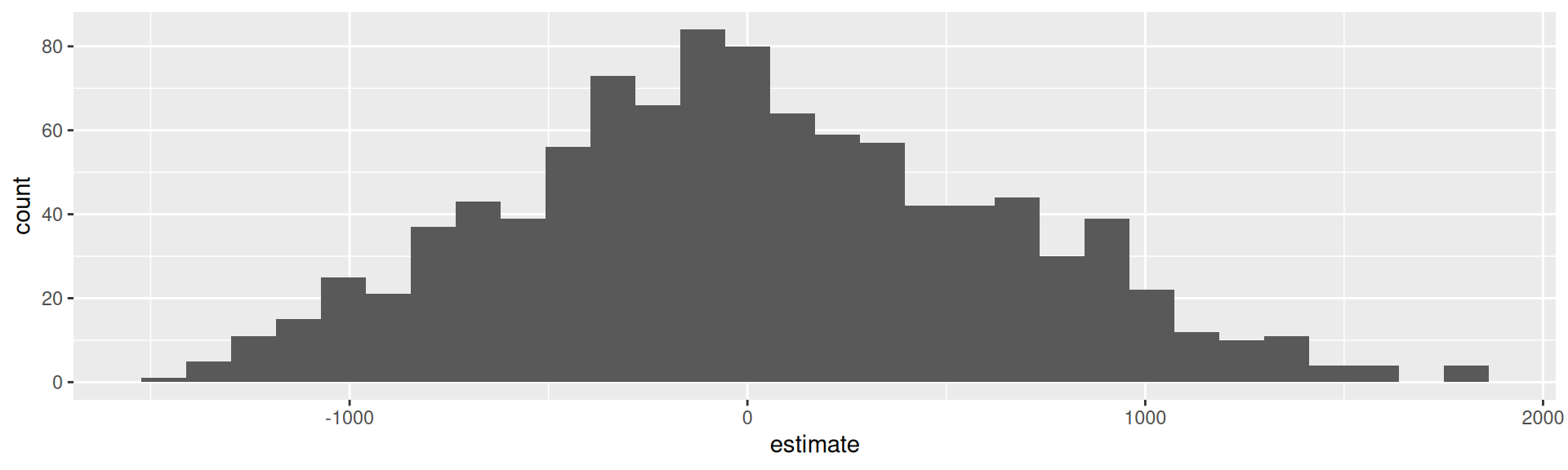
How does this work?
null_dist <- counties_sample |>
specify(mean_household_income ~ uninsured) |>
hypothesize(null = "independence") |>
generate(reps = 1000, type = "permute") |>
fit()
null_dist# A tibble: 2,000 × 3
# Groups: replicate [1,000]
replicate term estimate
<int> <chr> <dbl>
1 1 intercept 73680.
2 1 uninsured -279.
3 2 intercept 71343.
4 2 uninsured -35.3
5 3 intercept 69869.
6 3 uninsured 118.
7 4 intercept 62820.
8 4 uninsured 853.
9 5 intercept 84203.
10 5 uninsured -1376.
# ℹ 1,990 more rowsHow does this work?
How does this work?
How does this work?
What is happening?
-
Recall: Bootstrapping for confidence intervals
We created a bunch of new data sets by resampling from our original data set
We computed an estimate for each new data set
-
Here:
We are creating a bunch of new data sets by permuting our original data set and computing an estimate for each
Instead of attempting to mimic samples from the population data (like boostrapping), we are attempting to mimic samples from the null
So what does “permuting” do?
We are simulating what the world would look like if the null hypothesis were true: what if mean_household_income and uninsured are unrelated?
- We randomly shuffle the values of the response variable:
mean_household_income - We leave the explanatory variable (
uninsured) unchanged - We do this many times (e.g.
reps = 1000) - Each time we calculate the slope from the new fake dataset
Small permutation example:
Original:
| Uninsured (%) | Mean Income ($k) |
|---|---|
| 5 | 70 |
| 8 | 65 |
| 6 | 68 |
| 7 | 66 |
| 9 | 64 |
Small permutation example:
Original:
| Uninsured (%) | Mean Income ($k) |
|---|---|
| 5 | 70 |
| 8 | 65 |
| 6 | 68 |
| 7 | 66 |
| 9 | 64 |
Permutation 1:
| Uninsured (%) | Mean Income ($k) |
|---|---|
| 8 | 70 |
| 5 | 65 |
| 7 | 68 |
| 9 | 66 |
| 6 | 64 |
Small permutation example:
Original:
| Uninsured (%) | Mean Income ($k) |
|---|---|
| 5 | 70 |
| 8 | 65 |
| 6 | 68 |
| 7 | 66 |
| 9 | 64 |
Permutation 2:
| Uninsured (%) | Mean Income ($k) |
|---|---|
| 5 | 70 |
| 7 | 65 |
| 9 | 68 |
| 8 | 66 |
| 6 | 64 |
. . .
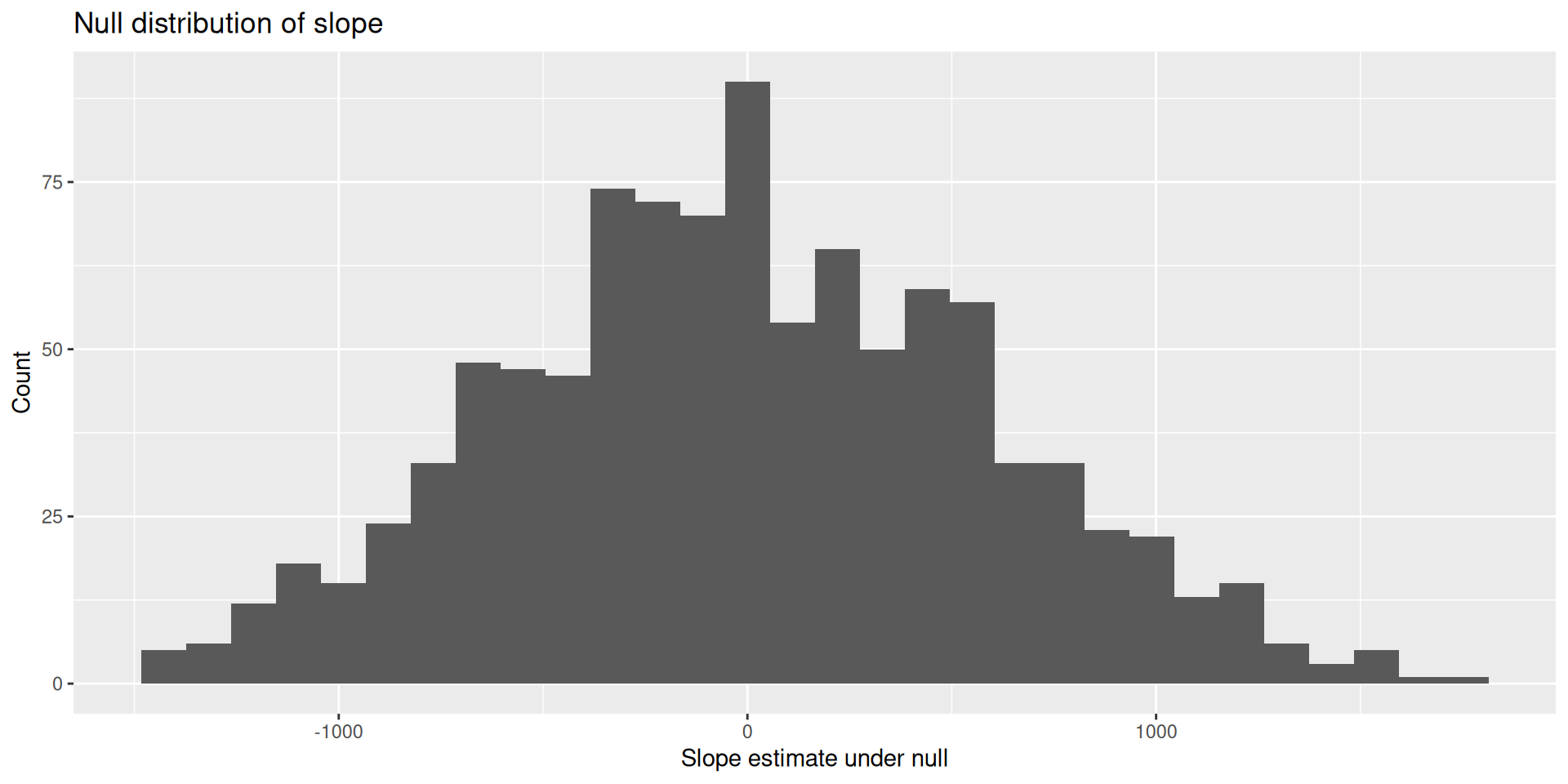
Do this reps times; make a histogram of slope estimates!
Null distribution
The null distribution shows the plot of
Then what?
Compare the slope from the original data set to our null distribution!
Better code
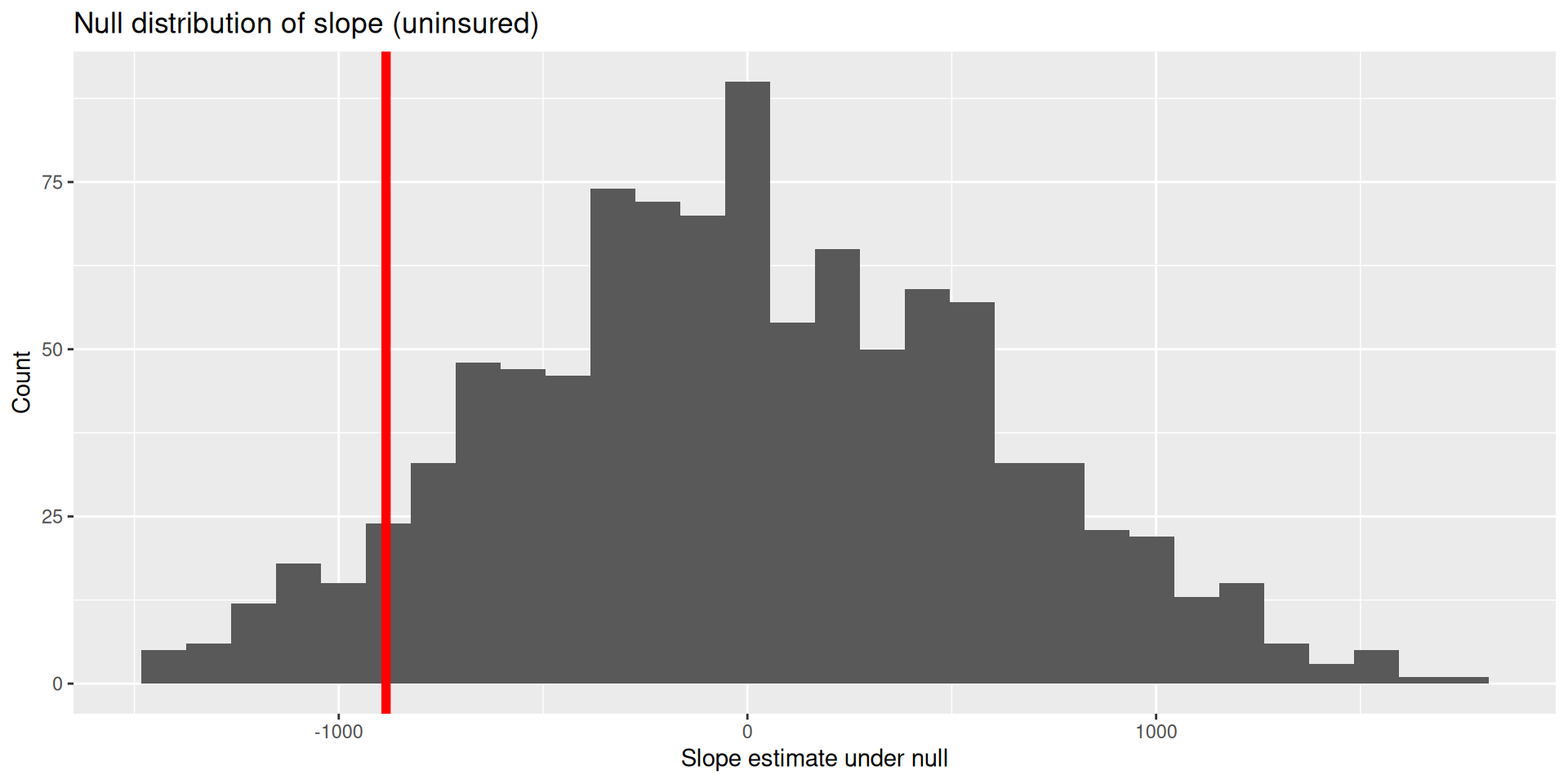
visualize(null_dist) +
shade_p_value(obs_stat = observed_fit, direction = "two-sided")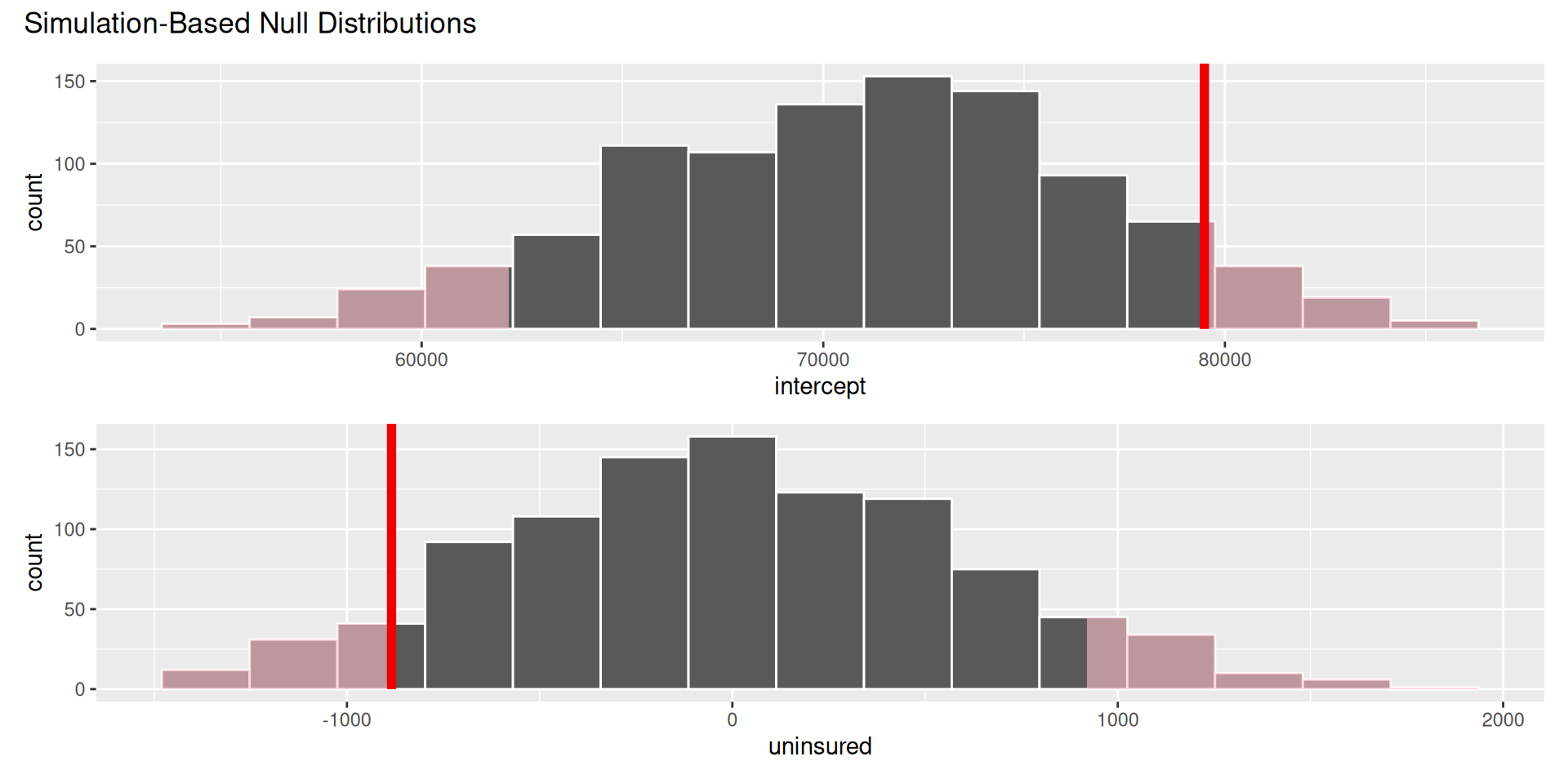
The p-value
null_dist |>
get_p_value(obs_stat = observed_fit, direction = "two-sided")# A tibble: 2 × 2
term p_value
<chr> <dbl>
1 intercept 0.138
2 uninsured 0.138Recap: Hypothesis testing
-
Think hypothetically: if the null hypothesis were in fact true, would my results be out of the ordinary?
- if no, then the null could be true;
- if yes, then the null might be bogus;
My results represent the reality of actual data. If they conflict with the null, then you throw out the null and stick with reality;
How do we quantify “would my results be out of the ordinary”?
Idea: Hypothesis test for a difference in means
What if I want to test if the means of two groups are actually different from each other?
- Is the mean household income different in counties that vote red vs. blue?
- Do athletes who train over a certain number of hours a day have better performance (measured by some metric) than those who train under that number?
- Do babies born to mothers who smoke have lower body weights than non-smoking mothers?
Example: smoking/non-smoking mothers
A random sample of US births from 2014:
births14 <- births14 |> drop_na(weight, habit)
births14# A tibble: 981 × 13
fage mage mature weeks premie visits gained weight lowbirthweight
<int> <dbl> <chr> <dbl> <chr> <dbl> <dbl> <dbl> <chr>
1 34 34 young… 37 full … 14 28 6.96 not low
2 36 31 young… 41 full … 12 41 8.86 not low
3 37 36 matur… 37 full … 10 28 7.51 not low
4 NA 16 young… 38 full … NA 29 6.19 not low
5 32 31 young… 36 premie 12 48 6.75 not low
6 32 26 young… 39 full … 14 45 6.69 not low
7 37 36 matur… 36 premie 10 20 6.13 not low
8 29 24 young… 40 full … 13 65 6.74 not low
9 30 32 young… 39 full … 15 25 8.94 not low
10 29 26 young… 39 full … 11 22 9.12 not low
# ℹ 971 more rows
# ℹ 4 more variables: sex <chr>, habit <chr>, marital <chr>,
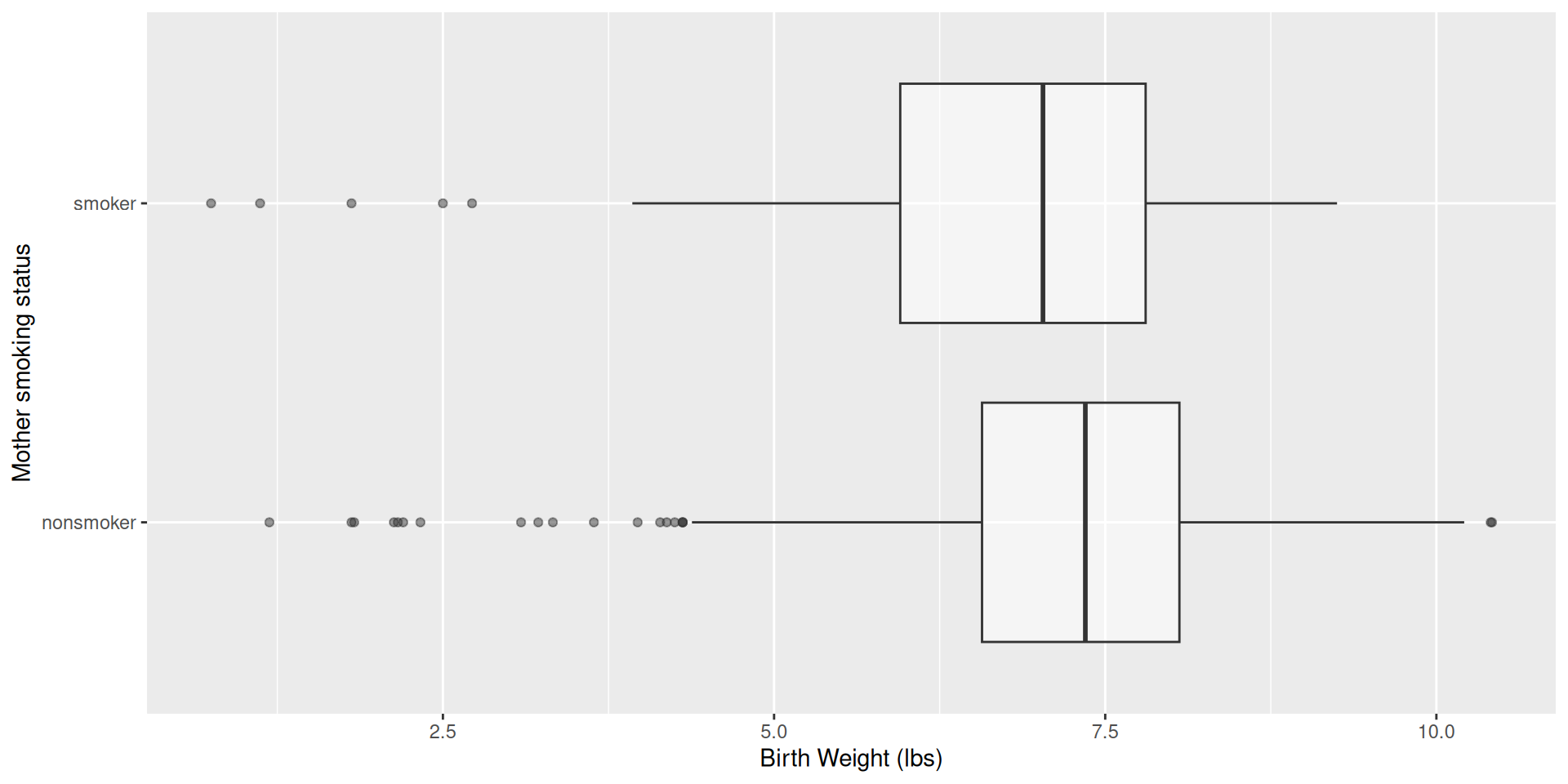
# whitemom <chr>Do babies born to mothers who smoke have lower body weights than non-smoking mothers?
Visualize
births14 |>
ggplot(aes(x = weight, y = habit)) +
geom_boxplot(alpha = 0.5) +
labs(
x = "Birth Weight (lbs)",
y = "Mother smoking status"
)
Estimate
linear_reg() |>
fit(weight ~ habit, data = births14) |>
tidy()# A tibble: 2 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) 7.27 0.0435 167. 0
2 habitsmoker -0.593 0.128 -4.65 0.00000382\[ \widehat{weight}=7.27-0.59\times \texttt{smoker}. \]
Remember…
\[ \widehat{weight}=7.27-0.59\times \texttt{smoker}. \]
habitis categorical with two levels:smokerandnon-smoker.The baseline is
non-smoker, with \[ \widehat{weight} = 7.27; \]The smoking group has
smoker = 1, so \[ \widehat{weight} = 7.27 - 0.59 = 6.68. \]
Those were not magic numbers
births14 |>
group_by(habit) |>
summarize(
mean_weight = mean(weight)
)# A tibble: 2 × 2
habit mean_weight
<chr> <dbl>
1 nonsmoker 7.27
2 smoker 6.68. . .
Don’t forget!
In a simple linear regression with a numerical response and a binary predictor, the slope estimate is the difference in the average response between the two groups.
Confidence interval
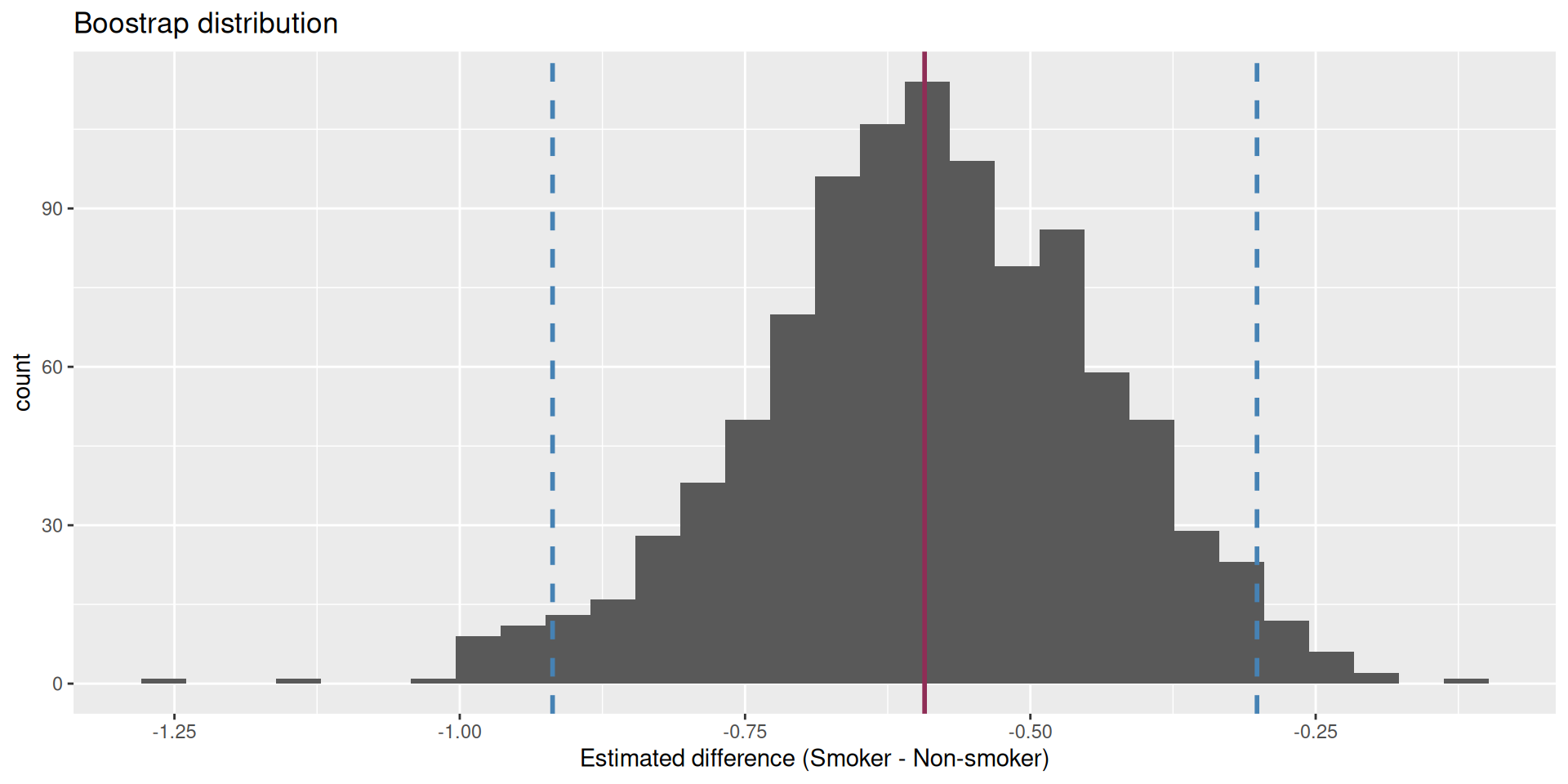
We are 95% confident that the true mean difference is between -0.919 and -0.301. This does not contain 0!!!
Competing claims
Are the data sufficiently informative to tell the difference between these two possibilities?
\[ \begin{aligned} H_0&: \beta_1=0 && (\text{no effect})\\ H_0&: \beta_1\neq0 && (\text{some effect})\\ \end{aligned} \]
- \(\beta_1\) is the difference in mean response between the smoking and non-smoking group;
- the alternative does not specify if the effect is positive or negative;
- the alternative does not specify that the effect is “large”.
Hypothesis test
. . .
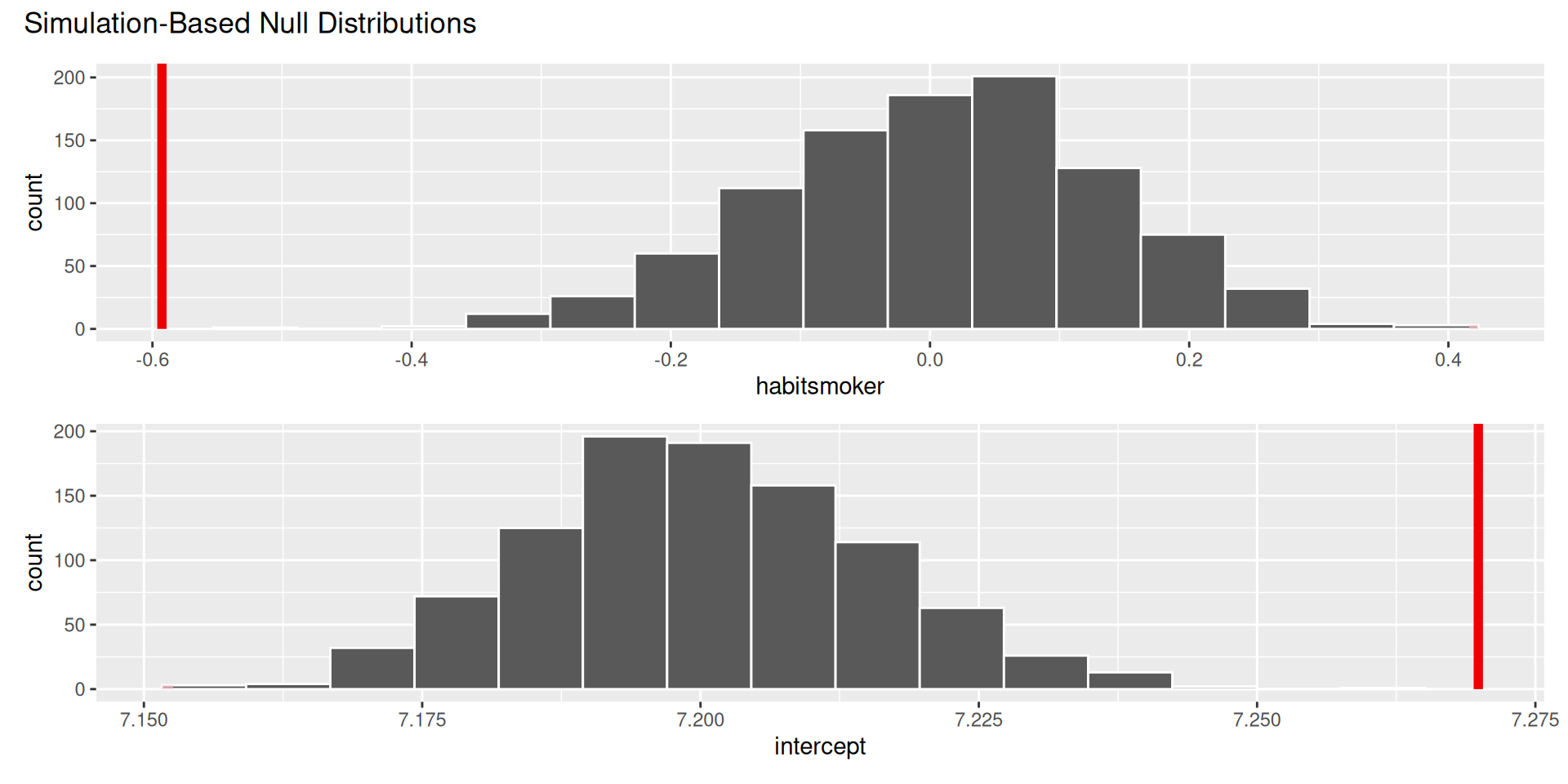
The p-value is basically zero.
What did we learn?
Evidence is sufficient to reject the null: smoking during pregnancy is associated with a difference in birth weight;
Is smoking causing birth weight to change?
The data are observational, and there are many unmeasured factors that could bear on both
habitandweight.Maybe there is a causal relationship, and maybe it can be teased out with data like these, but it is not so straightforward
. . .
Just because there is a statistically discernible association does not mean there is a causal relationship.
So, when can we draw causal conclusions?
-
Best hope: run a controlled, randomized experiment:
- get a big, representative, random sample from target population;
- randomly divide subjects into treatment and control;
- difference in outcomes was caused by the treatment alone;
- but this may be too costly or unethical.
-
Observational data are very challenging:
- you couldn’t control gosh darned thing;
- different outcomes could be caused by confounding factors, which you may or may not have measured.
A proper, controlled experiment
Does treatment using embryonic stem cells (ESCs) help improve heart function following a heart attack? Each sheep in the study was randomly assigned to the ESC or control group, and the change in their hearts’ pumping capacity was measured in the study. A positive value corresponds to increased pumping capacity, which generally suggests a stronger recovery.
. . .
glimpse(stem_cell)Rows: 18
Columns: 3
$ trmt <fct> ctrl, ctrl, ctrl, ctrl, ctrl, ctrl, ctrl, ctrl, ctrl,…
$ before <dbl> 35.25, 36.50, 39.75, 39.75, 41.75, 45.00, 47.00, 52.0…
$ after <dbl> 29.50, 29.50, 36.25, 38.00, 37.50, 42.75, 39.00, 45.2…Visualize
stem_cell <- stem_cell |>
mutate(change = after - before)
ggplot(stem_cell, aes(x = change, y = trmt)) +
geom_boxplot()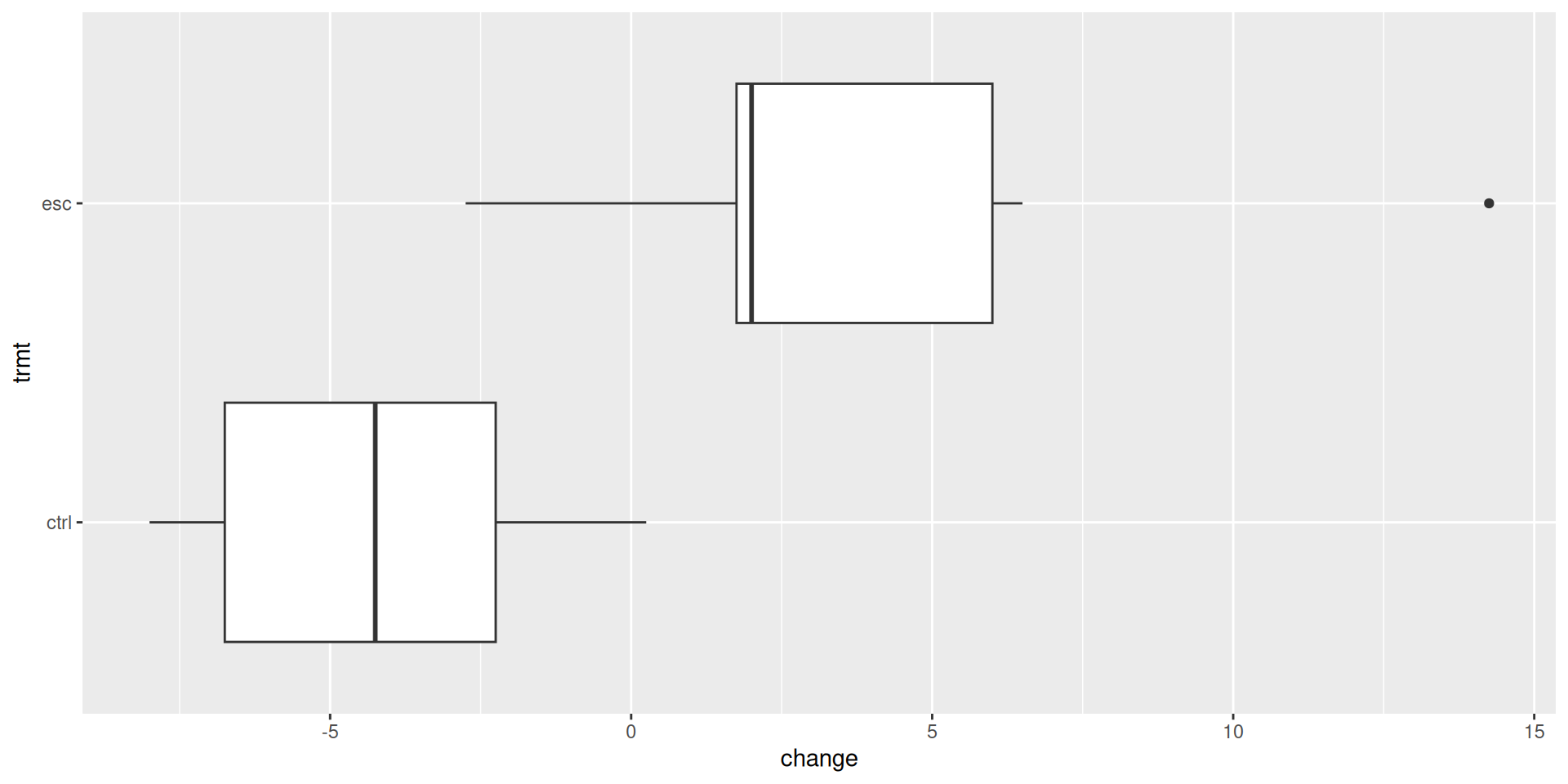
Model fit
linear_reg() |>
fit(change ~ trmt, data = stem_cell) |>
tidy()# A tibble: 2 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) -4.33 1.38 -3.14 0.00639
2 trmtesc 7.83 1.95 4.01 0.00102\[ \widehat{change}=-4.33+7.83\times \texttt{esc} \]
Remember…
\[ \widehat{change}=-4.33+7.83\times \texttt{esc} \]
trmtis categorical with two levels:ctrl(0) andesc(1).The control group has
esc = 0, so \[ \widehat{change} = -4.33; \]The treatment group has
esc = 1, so \[ \widehat{change} = -4.33+7.83=3.5. \]
Again, those were not magic numbers!!
stem_cell |>
group_by(trmt) |>
summarize(
mean_change = mean(change)
)# A tibble: 2 × 2
trmt mean_change
<fct> <dbl>
1 ctrl -4.33
2 esc 3.5 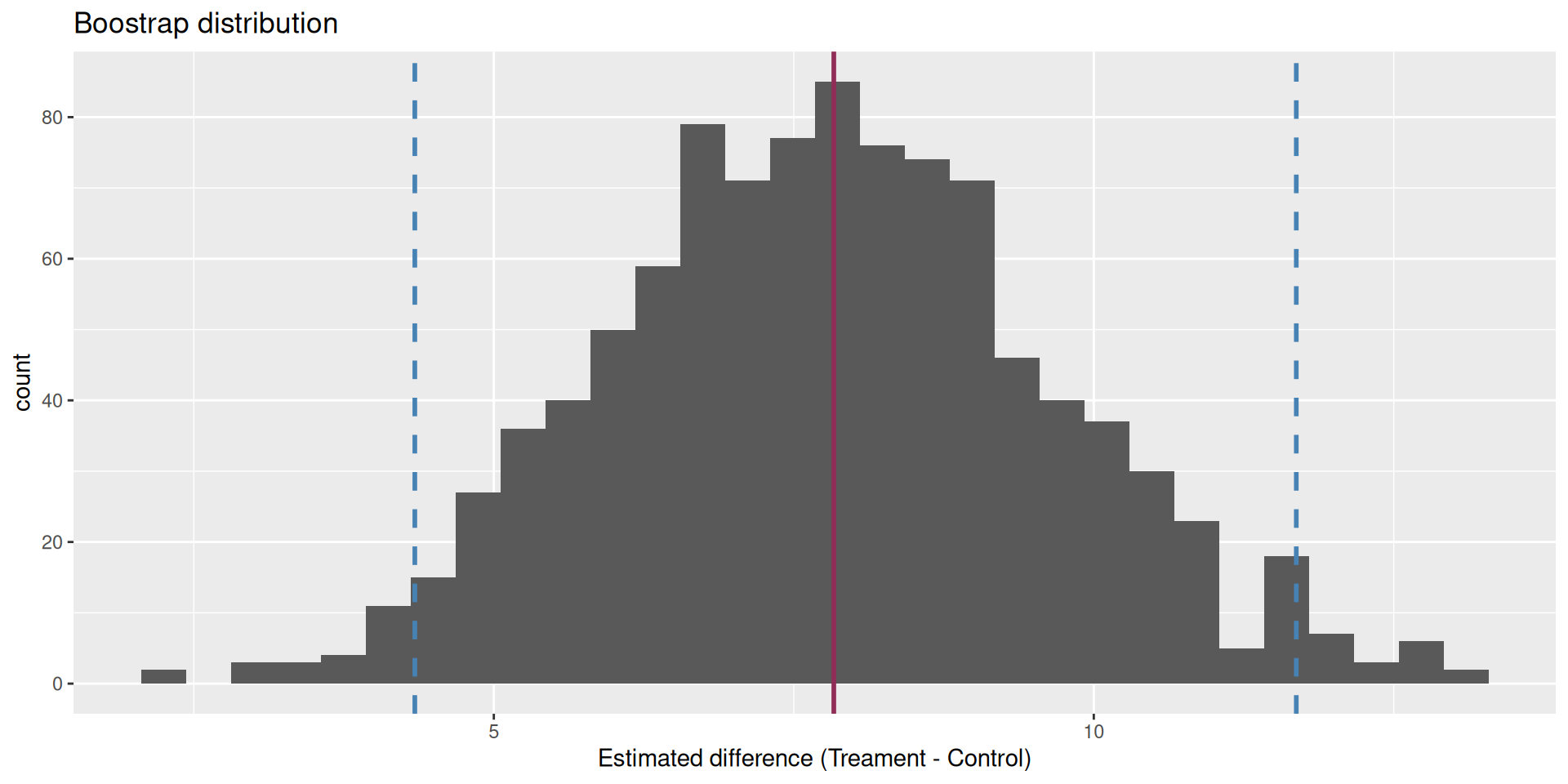Confidence interval
We are 95% confident that the true mean difference is between 4.34 and 11.7.
Competing claims: again!
Are the data sufficiently informative to tell the difference between these two possibilities?
\[ \begin{aligned} H_0&: \beta_1=0 && (\text{no effect})\\ H_0&: \beta_1\neq0 && (\text{some effect})\\ \end{aligned} \]
- \(\beta_1\) is the difference in mean response between the treatment and control group;
- the alternative does not specify if the effect is positive or negative;
- the alternative does not specify that the effect is “large”.
Hypothesis test
. . .
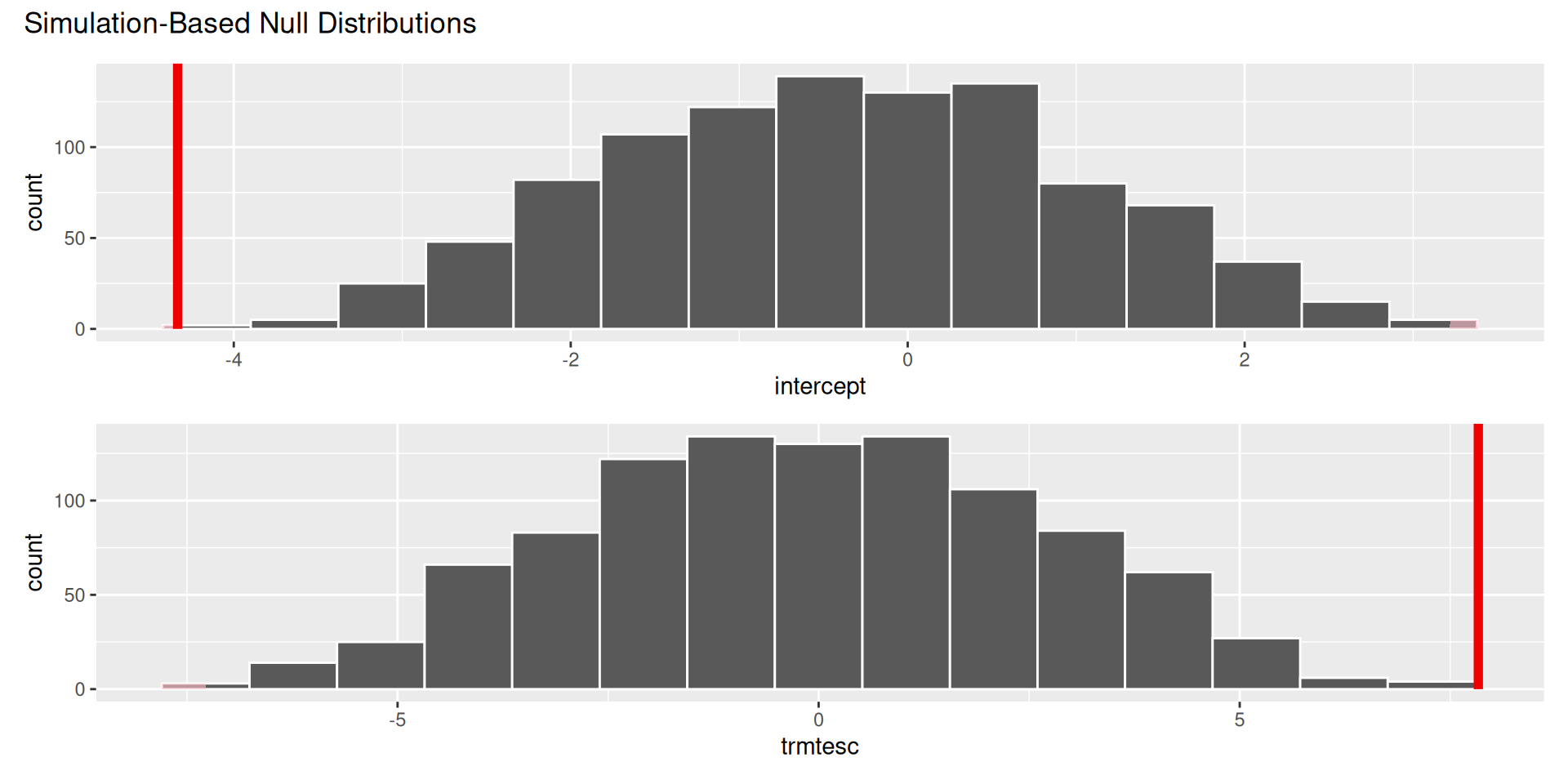
The p-value is basically zero.
What did we learn?
In a hypothetical world where the treatment has no effect, it would be very unlikely to get results like the ones we did;
Evidence is sufficient to reject the null. There is some effect;
If you are convinced by the experimental design, the effect is causal;
Is the effect large and meaningful and something you should base major decisions on? Statistics cannot answer that question!
AE !
Today’s AE: Inference Overview
Announcements
I am filling in for Mary’s OH today!!
Do your second peer feedback forms!!
Come to lab on Friday!!!