Lecture 19
Go to your ae project in RStudio.
Make sure all of your changes up to this point are committed and pushed, i.e., there’s nothing left in your Git pane.
Click Pull to get today’s application exercise file: ae-14-spam-filter.qmd.
Wait till the you’re prompted to work on the application exercise during class before editing the file.
Office hours tomorrow will be about 20 mins short (1:00 - 2:40). I will be there a little before 1:00 if you want to come early!
Make appointment to see in-class exams/talk through problems you’re stuck on. Remember, final exam is cumulative!!
Milestone 3 due Friday night!!
Once your project website renders, you still need to push for the changes to show up!!!
Goal: modelling/predicting binary outcome \(y\)
. . .
\[ \hat{p} = \frac{e^{b_0+b_1x}}{1+e^{b_0+b_1x}}. \]
. . .
\[ \log\left(\frac{\hat{p}}{1-\hat{p}}\right) = b_0+b_1x. \]
simple_logistic_fit <- logistic_reg() |>
fit(spam ~ exclaim_mess, data = email)
tidy(simple_logistic_fit)# A tibble: 2 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) -2.27 0.0553 -41.1 0
2 exclaim_mess 0.000272 0.000949 0.287 0.774. . .
Fitted equation for the log-odds:
\[ \log\left(\frac{\hat{p}}{1-\hat{p}}\right) = -2.27 + 0.000272\times exclaim~mess \]
. . .
Interpretations are strange and delicate.
AE-14: Watch now, fill in later (optional!)
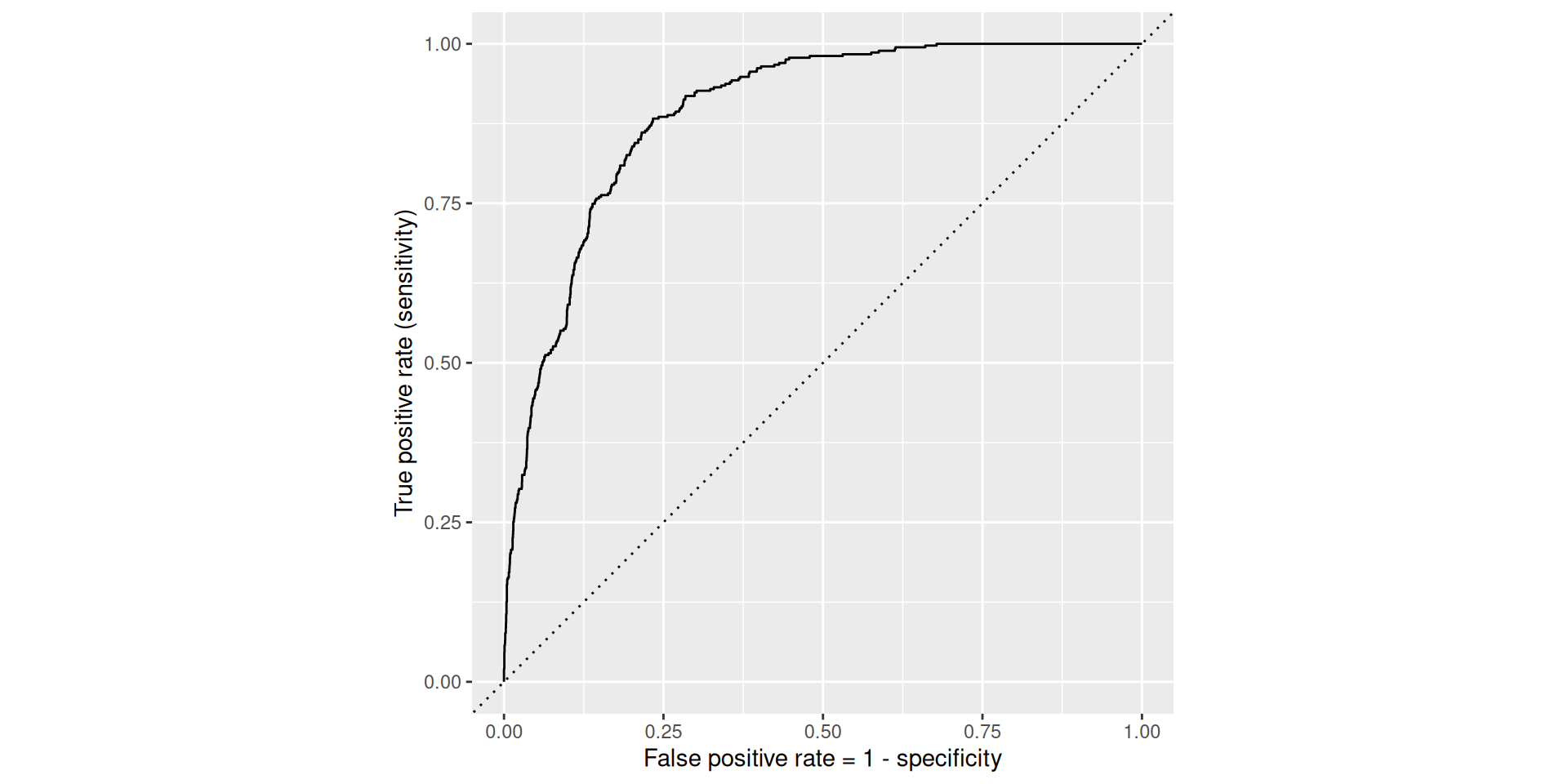
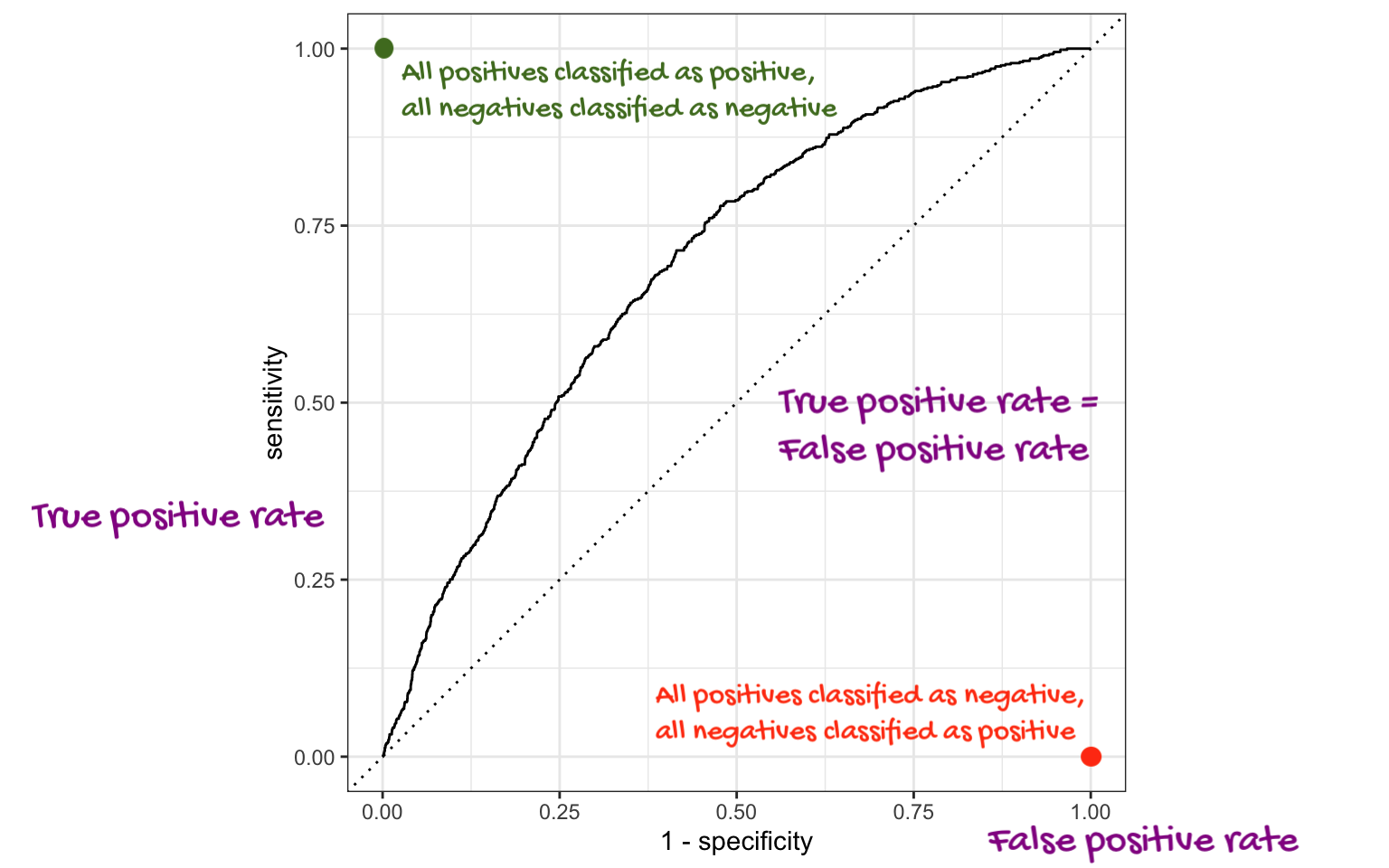
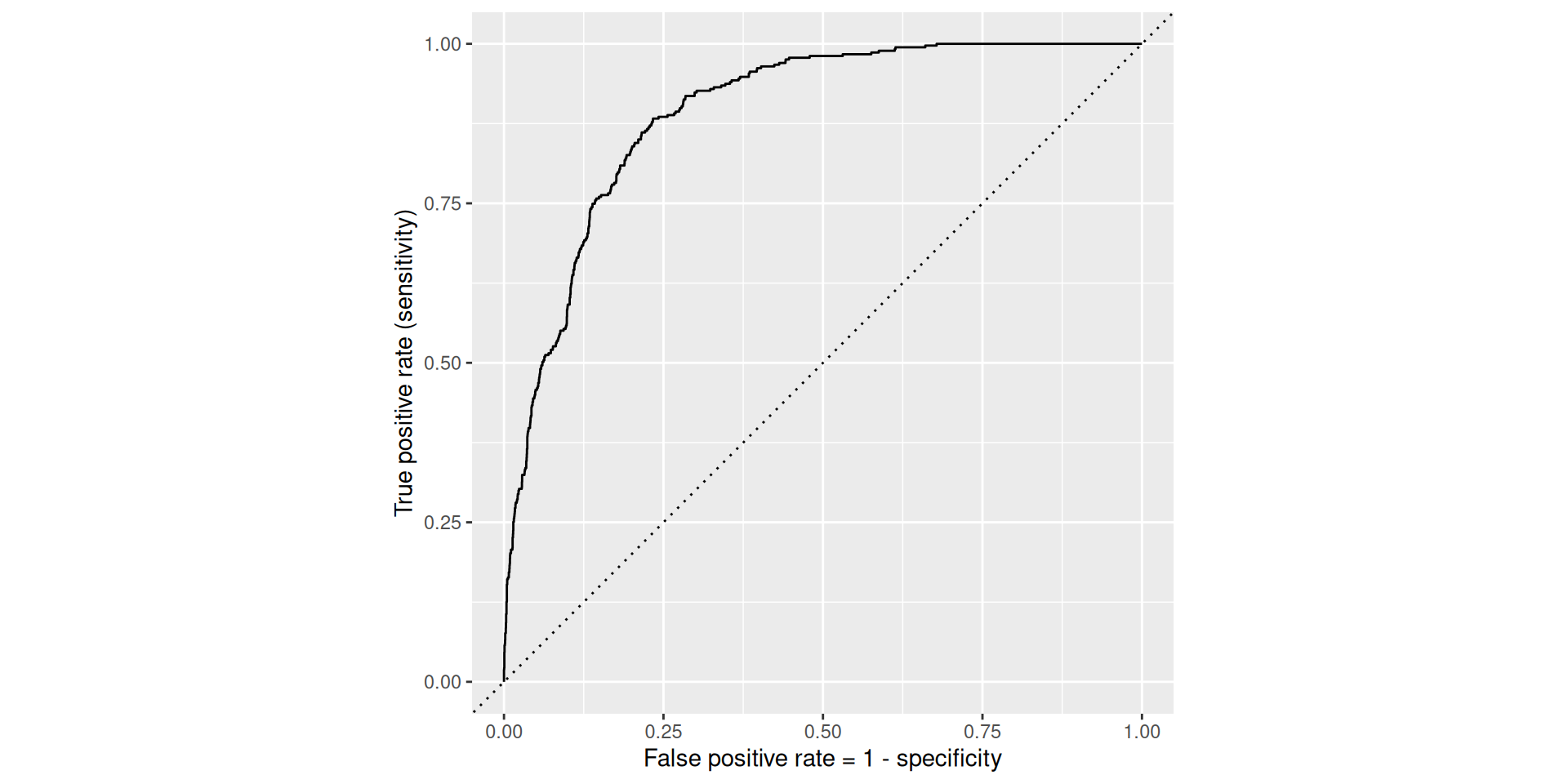
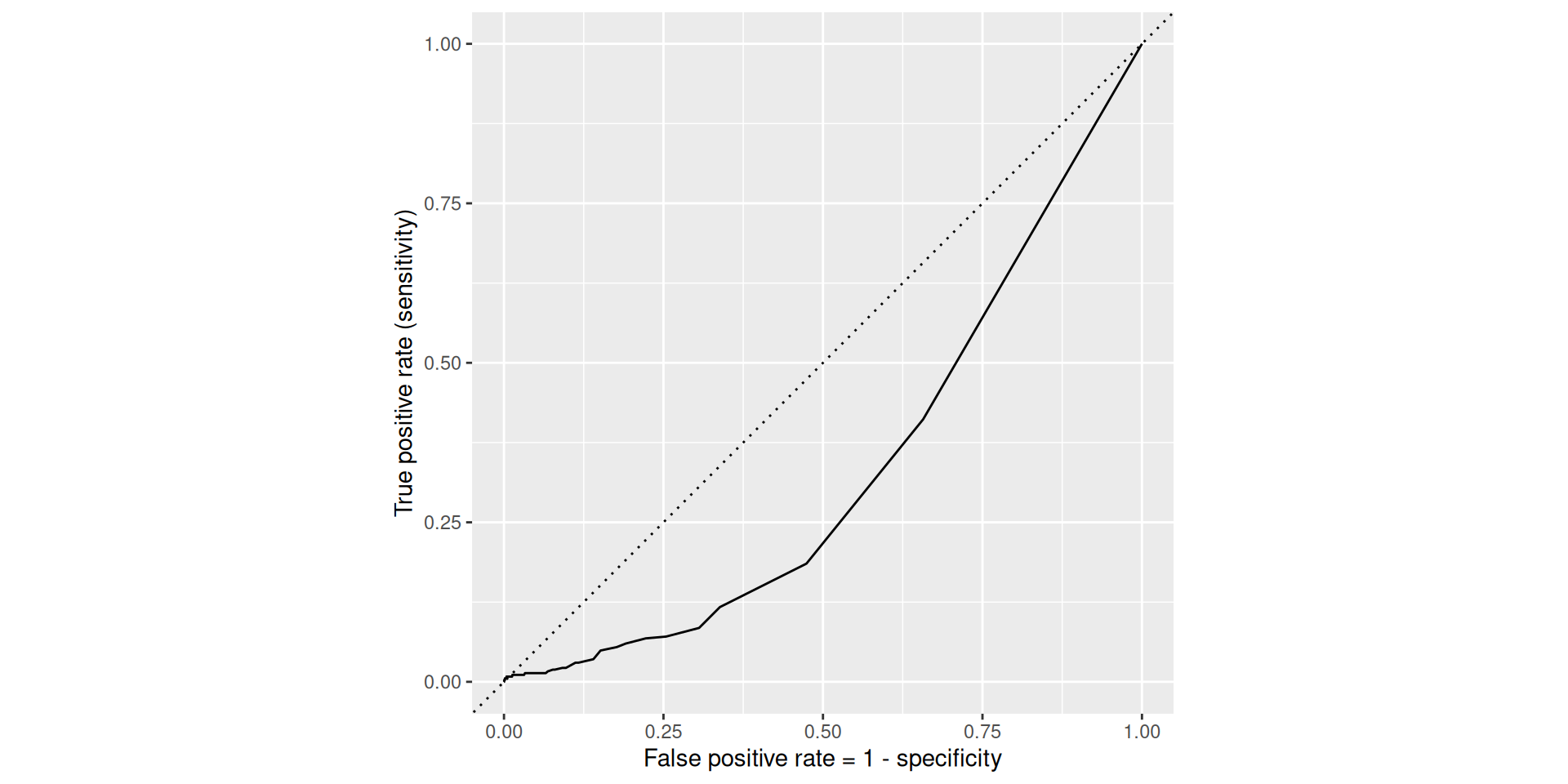
exclaim_mess) to predict whether or not the email is spam (spam: 1 if spam; 0 if not)glimpse(email)Rows: 3,921
Columns: 21
$ spam <fct> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
$ to_multiple <fct> 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0,…
$ from <fct> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,…
$ cc <int> 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 2, 1,…
$ sent_email <fct> 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 0, 1,…
$ time <dttm> 2012-01-01 06:16:41, 2012-01-01 07:03:59, 2012…
$ image <dbl> 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0,…
$ attach <dbl> 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0,…
$ dollar <dbl> 0, 0, 4, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 0,…
$ winner <fct> no, no, no, no, no, no, no, no, no, no, no, no,…
$ inherit <dbl> 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
$ viagra <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
$ password <dbl> 0, 0, 0, 0, 2, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
$ num_char <dbl> 11.370, 10.504, 7.773, 13.256, 1.231, 1.091, 4.…
$ line_breaks <int> 202, 202, 192, 255, 29, 25, 193, 237, 69, 68, 2…
$ format <fct> 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1,…
$ re_subj <fct> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1,…
$ exclaim_subj <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
$ urgent_subj <fct> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
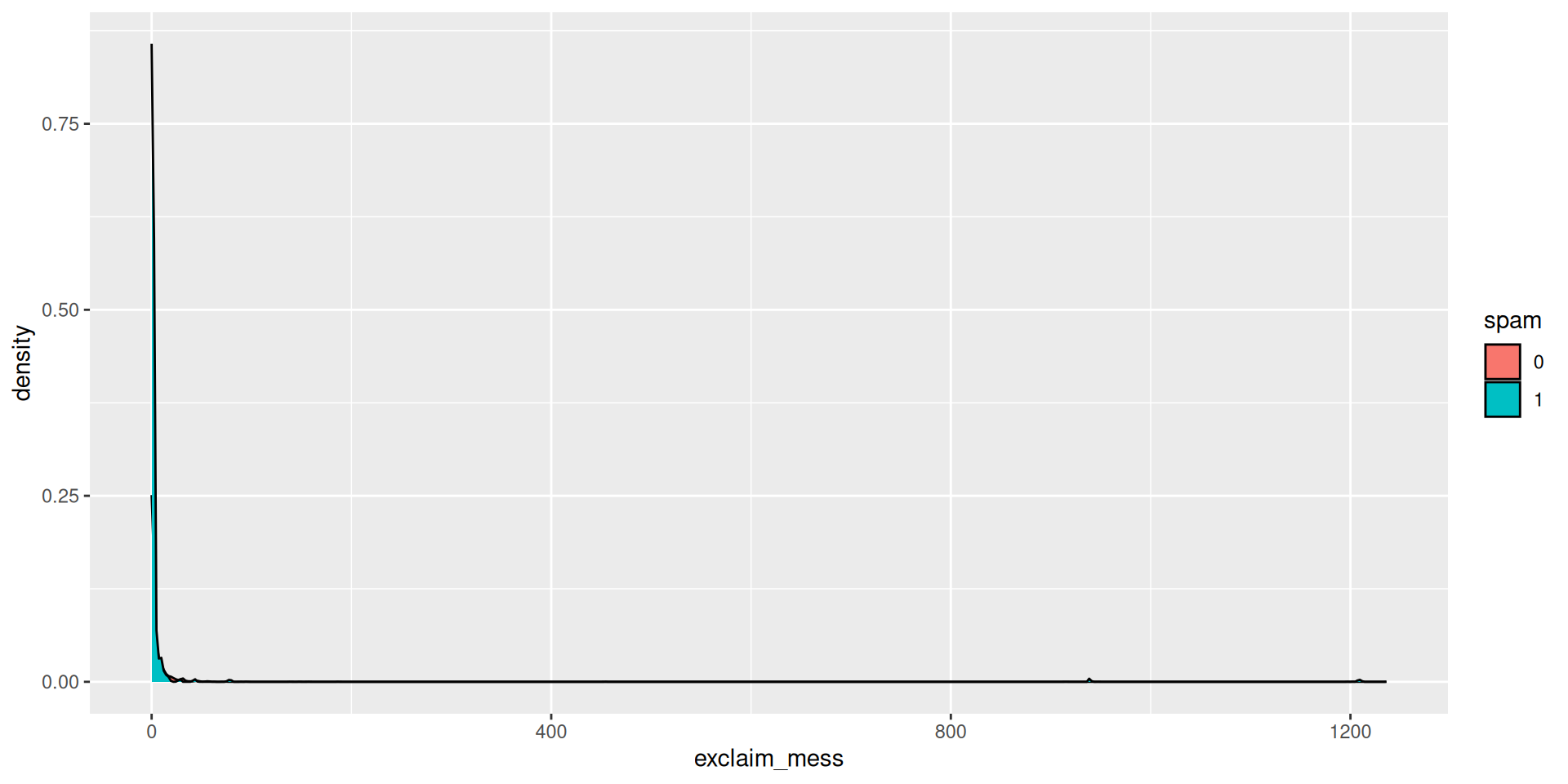
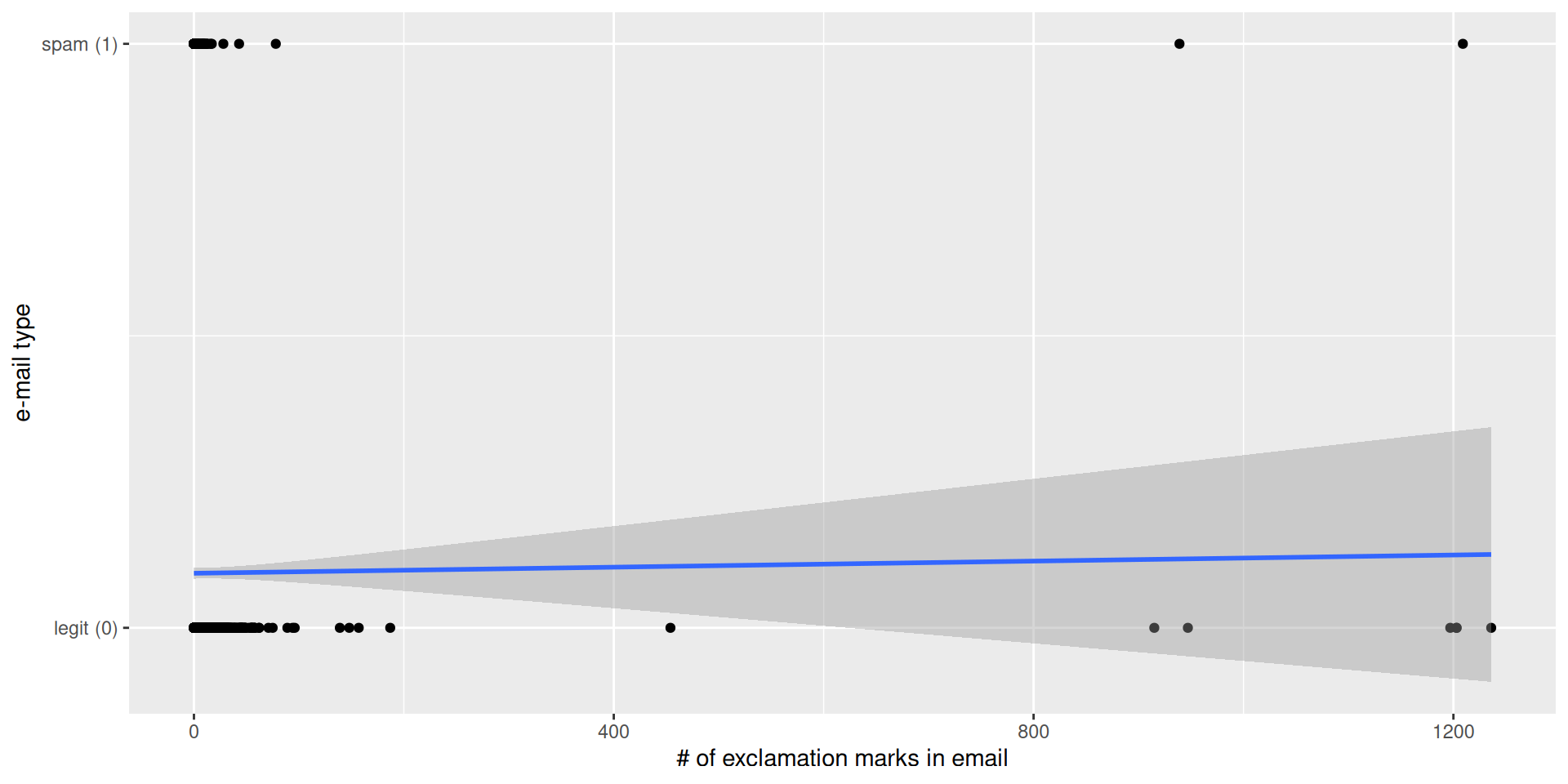
$ exclaim_mess <dbl> 0, 1, 6, 48, 1, 1, 1, 18, 1, 0, 2, 1, 0, 10, 4,…
$ number <fct> big, small, small, small, none, none, big, smal…
Mean exclamation points by spam/not spam:
# A tibble: 2 × 2
spam mean_ep
<fct> <dbl>
1 0 6.51
2 1 7.32
This makes no sense at all.
This is what we have seen already!
spam_exl_fit <- logistic_reg() |>
fit(spam ~ exclaim_mess, data = email)
tidy(spam_exl_fit)# A tibble: 2 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) -2.27 0.0553 -41.1 0
2 exclaim_mess 0.000272 0.000949 0.287 0.774\[ \log\left(\frac{\hat{p}}{1-\hat{p}}\right) = -2.27 + 0.000272\times exclaim~mess \]
What is the probability the email is spam if it contains 10 exclamation points?? Use predict!
new_email <- tibble(
exclaim_mess = 10
)
new_email# A tibble: 1 × 1
exclaim_mess
<dbl>
1 10What is the probability the email is spam if it contains 10 exclamation points?? Use predict!
new_email <- tibble(
exclaim_mess = 10
)
predict(spam_exl_fit, new_data = new_email, type = "prob")# A tibble: 1 × 2
.pred_0 .pred_1
<dbl> <dbl>
1 0.906 0.0937A probability is nice, but we want an actual decision. Classify the email!!!
predict(spam_exl_fit, new_data = new_email, type = "class")# A tibble: 1 × 1
.pred_class
<fct>
1 0 . . .
The default behavior is to threshold the probabilities by 0.5.
Why limit ourselves to using exclamation points???
spam_fit <- logistic_reg() |>
fit(spam ~ time + exclaim_mess + line_breaks, data = email)What about all the predictors???
spam_all_fit <- logistic_reg() |>
fit(spam ~ ., data = email)Warning: glm.fit: fitted probabilities numerically 0 or 1 occurredThe . means all other variables .
There are two kinds of mistakes:
We want to avoid both, but there’s a trade-off.
False negative rate is the proportion of actual positives that were classified as negatives.
False positive rate is the proportion of actual negatives that were classified as positives.
. . .
We want these to be low!
False negative rate = \(\frac{FN}{FN + TP}\)
False positive rate = \(\frac{FP}{FP + TN}\)
Sensitivity is the proportion of actual positives that were correctly classified as positive.
Also known as true positive rate and recall
Sensitivity = \(\frac{FN}{FN + TP}\)
Sensitivity = 1 − False negative rate
Useful when false negatives are more “expensive” than false positives
We want this to be high!
Specificity is the proportion of actual negatives that were correctly classified as negative
Also known as true negative rate
Specificity = \(\frac{TN}{FP + TN}\)
Specificity = 1 − False positive rate
Useful when false positives are more “expensive” than false negatives
We want this to be high!
The augment function takes a data frame and “augments” it by adding three new columns on the left that describe the model predictions for each row:
.pred_class: model prediction (\(\hat{y}\)) based on a 50% threshold;.pred_0: model estimate of \(P(y=0)\);.pred_1: model estimate of \(P(y=1) = 1 - P(y = 0)\).The augment function takes a data frame and “augments” it by adding three new columns on the left that describe the model predictions for each row:
spam_aug_all <- augment(spam_all_fit, email)
spam_aug_all# A tibble: 3,921 × 24
.pred_class .pred_0 .pred_1 spam to_multiple from cc
<fct> <dbl> <dbl> <fct> <fct> <fct> <int>
1 0 0.867 1.33e- 1 0 0 1 0
2 0 0.943 5.70e- 2 0 0 1 0
3 0 0.942 5.78e- 2 0 0 1 0
4 0 0.920 7.96e- 2 0 0 1 0
5 0 0.903 9.74e- 2 0 0 1 0
6 0 0.901 9.87e- 2 0 0 1 0
7 0 1.00 7.89e-12 0 1 1 0
8 0 1.00 1.24e-12 0 1 1 1
9 0 0.862 1.38e- 1 0 0 1 0
10 0 0.922 7.76e- 2 0 0 1 0
# ℹ 3,911 more rows
# ℹ 17 more variables: sent_email <fct>, time <dttm>, image <dbl>,
# attach <dbl>, dollar <dbl>, winner <fct>, inherit <dbl>,
# viagra <dbl>, password <dbl>, num_char <dbl>, line_breaks <int>,
# format <fct>, re_subj <fct>, exclaim_subj <dbl>,
# urgent_subj <fct>, exclaim_mess <dbl>, number <fct>spam_aug_all |>
count(spam, .pred_class) # A tibble: 4 × 3
spam .pred_class n
<fct> <fct> <int>
1 0 0 3521
2 0 1 33
3 1 0 299
4 1 1 68spam_aug_all |>
count(spam, .pred_class) |>
group_by(spam)# A tibble: 4 × 3
# Groups: spam [2]
spam .pred_class n
<fct> <fct> <int>
1 0 0 3521
2 0 1 33
3 1 0 299
4 1 1 68spam_aug_all |>
count(spam, .pred_class) |>
group_by(spam) |>
mutate(p = n / sum(n))# A tibble: 4 × 4
# Groups: spam [2]
spam .pred_class n p
<fct> <fct> <int> <dbl>
1 0 0 3521 0.991
2 0 1 33 0.00929
3 1 0 299 0.815
4 1 1 68 0.185 spam_aug_all |>
count(spam, .pred_class) |>
group_by(spam) |>
mutate(p = n / sum(n),
decision = case_when(
spam == "0" & .pred_class == "0" ~ "True negative",
spam == "0" & .pred_class == "1" ~ "False positive",
spam == "1" & .pred_class == "0" ~ "False negative",
spam == "1" & .pred_class == "1" ~ "True positive"
))# A tibble: 4 × 5
# Groups: spam [2]
spam .pred_class n p decision
<fct> <fct> <int> <dbl> <chr>
1 0 0 3521 0.991 True negative
2 0 1 33 0.00929 False positive
3 1 0 299 0.815 False negative
4 1 1 68 0.185 True positive This is where we have AE14 stop….
Augment uses a default 50% threshold.
. . .
If we change the classification threshold, we change the classifications, and we change the error rates:
. . .
If we repeat this process for “all” possible thresholds \(0\leq p^\star\leq 1\), we trace out the receiver operating characteristic curve (ROC curve), which assesses the model’s performance across a range of thresholds:
Which corner of the plot indicates the best model performance?
. . .
Upper left!
The farther up and to the left the ROC curve is, the better the classification accuracy. You can quantify this with the area under the curve.
Area under the ROC curve will be our “quality score” for comparing logistic regression models.
To determine whether we should include a predictor in a model, we should start by asking:
Is it ethical to use this variable? (Or even legal?)
Will this variable be available at prediction time?
Does this variable contribute to explainability?
So far, we’ve been using all the data we have for building models. In predictive contexts, this would be considered cheating.
Evaluating model performance for predicting outcomes that were used when building the models is like evaluating your learning with questions whose answers you’ve already seen.
For predictive models (used primarily in machine learning), we typically split data into training and test sets:
- The training set is used for EDA (plots, summary statistics, etc.)
The training set is used to estimate model parameters (fit models).
The test set is used to find an independent assessment of model performance. NEVER look at the test set during training.
The more data we spend (use in training), the better estimates we’ll get.
Spending too much data in training prevents us from computing a good assessment of predictive performance.
Spending too much data in testing prevents us from computing a good estimate of model parameters.
Randomly pick training and testing rows!
set.seed(20241112)
email_split <- initial_split(email)
email_split<Training/Testing/Total>
<2940/981/3921>. . .
Default: 75% training; 25% testing
Change proportion:
set.seed(20250612)
email_split <- initial_split(email, prop = 0.8)
email_split<Training/Testing/Total>
<3136/785/3921>What does set.seed() do?
To create that split of the data, R generates “pseudo-random” numbers: while they are made to behave like random numbers, their generation is deterministic given a “seed”.
This allows us to reproduce results by setting that seed.
Which seed you pick doesn’t matter, as long as you don’t try a bunch of seeds and pick the one that gives you the best performance.
email_train <- training(email_split)
email_test <- testing(email_split)email_train# A tibble: 3,136 × 21
spam to_multiple from cc sent_email time image
<fct> <fct> <fct> <int> <fct> <dttm> <dbl>
1 0 0 1 0 0 2012-02-18 19:20:54 0
2 1 0 1 0 0 2012-03-10 22:43:58 0
3 0 1 1 0 0 2012-03-06 14:10:00 0
4 1 0 1 0 0 2012-03-18 13:26:41 0
5 0 0 1 0 1 2012-03-16 00:47:33 0
6 0 0 1 0 1 2012-03-31 13:24:03 0
7 0 0 1 0 0 2012-02-16 16:25:22 0
8 0 0 1 0 0 2012-02-24 23:18:35 0
9 0 1 1 0 1 2012-01-22 09:02:27 0
10 0 0 1 0 0 2012-02-11 00:46:30 0
# ℹ 3,126 more rows
# ℹ 14 more variables: attach <dbl>, dollar <dbl>, winner <fct>,
# inherit <dbl>, viagra <dbl>, password <dbl>, num_char <dbl>,
# line_breaks <int>, format <fct>, re_subj <fct>,
# exclaim_subj <dbl>, urgent_subj <fct>, exclaim_mess <dbl>,
# number <fct>email_test# A tibble: 785 × 21
spam to_multiple from cc sent_email time image
<fct> <fct> <fct> <int> <fct> <dttm> <dbl>
1 0 1 1 1 1 2012-01-01 18:45:21 1
2 0 0 1 0 1 2012-01-01 18:23:44 0
3 0 0 1 1 1 2012-01-01 23:40:14 0
4 0 0 1 0 0 2012-01-02 02:51:24 0
5 0 0 1 2 0 2012-01-02 04:07:57 0
6 0 0 1 0 0 2012-01-02 14:35:56 0
7 0 0 1 0 0 2012-01-02 15:12:51 0
8 0 0 1 5 0 2012-01-02 17:48:26 0
9 0 1 1 1 0 2012-01-02 15:27:07 0
10 0 0 1 7 0 2012-01-03 00:07:51 0
# ℹ 775 more rows
# ℹ 14 more variables: attach <dbl>, dollar <dbl>, winner <fct>,
# inherit <dbl>, viagra <dbl>, password <dbl>, num_char <dbl>,
# line_breaks <int>, format <fct>, re_subj <fct>,
# exclaim_subj <dbl>, urgent_subj <fct>, exclaim_mess <dbl>,
# number <fct>The U.S. Forest Service maintains machine learning models to predict whether a plot of land is “forested.”
This classification is important for research, legislation, land management, etc. purposes.
Plots are typically remeasured every 10 years.
The forested dataset contains the most recent measurement per plot.
forested
forested# A tibble: 7,107 × 19
forested year elevation eastness northness roughness tree_no_tree
<fct> <dbl> <dbl> <dbl> <dbl> <dbl> <fct>
1 Yes 2005 881 90 43 63 Tree
2 Yes 2005 113 -25 96 30 Tree
3 No 2005 164 -84 53 13 Tree
4 Yes 2005 299 93 34 6 No tree
5 Yes 2005 806 47 -88 35 Tree
6 Yes 2005 736 -27 -96 53 Tree
7 Yes 2005 636 -48 87 3 No tree
8 Yes 2005 224 -65 -75 9 Tree
9 Yes 2005 52 -62 78 42 Tree
10 Yes 2005 2240 -67 -74 99 No tree
# ℹ 7,097 more rows
# ℹ 12 more variables: dew_temp <dbl>, precip_annual <dbl>,
# temp_annual_mean <dbl>, temp_annual_min <dbl>,
# temp_annual_max <dbl>, temp_january_min <dbl>, vapor_min <dbl>,
# vapor_max <dbl>, canopy_cover <dbl>, lon <dbl>, lat <dbl>,
# land_type <fct>forested
glimpse(forested)Rows: 7,107
Columns: 19
$ forested <fct> Yes, Yes, No, Yes, Yes, Yes, Yes, Yes, Yes,…
$ year <dbl> 2005, 2005, 2005, 2005, 2005, 2005, 2005, 2…
$ elevation <dbl> 881, 113, 164, 299, 806, 736, 636, 224, 52,…
$ eastness <dbl> 90, -25, -84, 93, 47, -27, -48, -65, -62, -…
$ northness <dbl> 43, 96, 53, 34, -88, -96, 87, -75, 78, -74,…
$ roughness <dbl> 63, 30, 13, 6, 35, 53, 3, 9, 42, 99, 51, 19…
$ tree_no_tree <fct> Tree, Tree, Tree, No tree, Tree, Tree, No t…
$ dew_temp <dbl> 0.04, 6.40, 6.06, 4.43, 1.06, 1.35, 1.42, 6…
$ precip_annual <dbl> 466, 1710, 1297, 2545, 609, 539, 702, 1195,…
$ temp_annual_mean <dbl> 6.42, 10.64, 10.07, 9.86, 7.72, 7.89, 7.61,…
$ temp_annual_min <dbl> -8.32, 1.40, 0.19, -1.20, -5.98, -6.00, -5.…
$ temp_annual_max <dbl> 12.91, 15.84, 14.42, 15.78, 13.84, 14.66, 1…
$ temp_january_min <dbl> -0.08, 5.44, 5.72, 3.95, 1.60, 1.12, 0.99, …
$ vapor_min <dbl> 78, 34, 49, 67, 114, 67, 67, 31, 60, 79, 17…
$ vapor_max <dbl> 1194, 938, 754, 1164, 1254, 1331, 1275, 944…
$ canopy_cover <dbl> 50, 79, 47, 42, 59, 36, 14, 27, 82, 12, 74,…
$ lon <dbl> -118.6865, -123.0825, -122.3468, -121.9144,…
$ lat <dbl> 48.69537, 47.07991, 48.77132, 45.80776, 48.…
$ land_type <fct> Tree, Tree, Tree, Tree, Tree, Tree, Non-tre…forested - Factor, Yes or No
levels(forested$forested)[1] "Yes" "No" Predictors: 18 remotely-sensed and easily-accessible predictors:
numeric variables based on weather and topography
categorical variables based on classifications from other governmental organizations
?forested