AE 12: Modelling penguins

Part 1

Our goal is to understand better how various body measurements and attributes of penguins relate to their body mass. First, we are going to investigate the relationship between a penguins’ flipper lengths and their body masses.

Based on our research focus, body mass is the response variable.

Task 1 - Exploratory Data Analysis: Visualize the relationship between flipper length and body mass of penguins.

ggplot(penguins, aes(x = flipper_length_mm, y = body_mass_g)) +
  geom_point()

Warning: Removed 2 rows containing missing values or values outside the scale range
(`geom_point()`).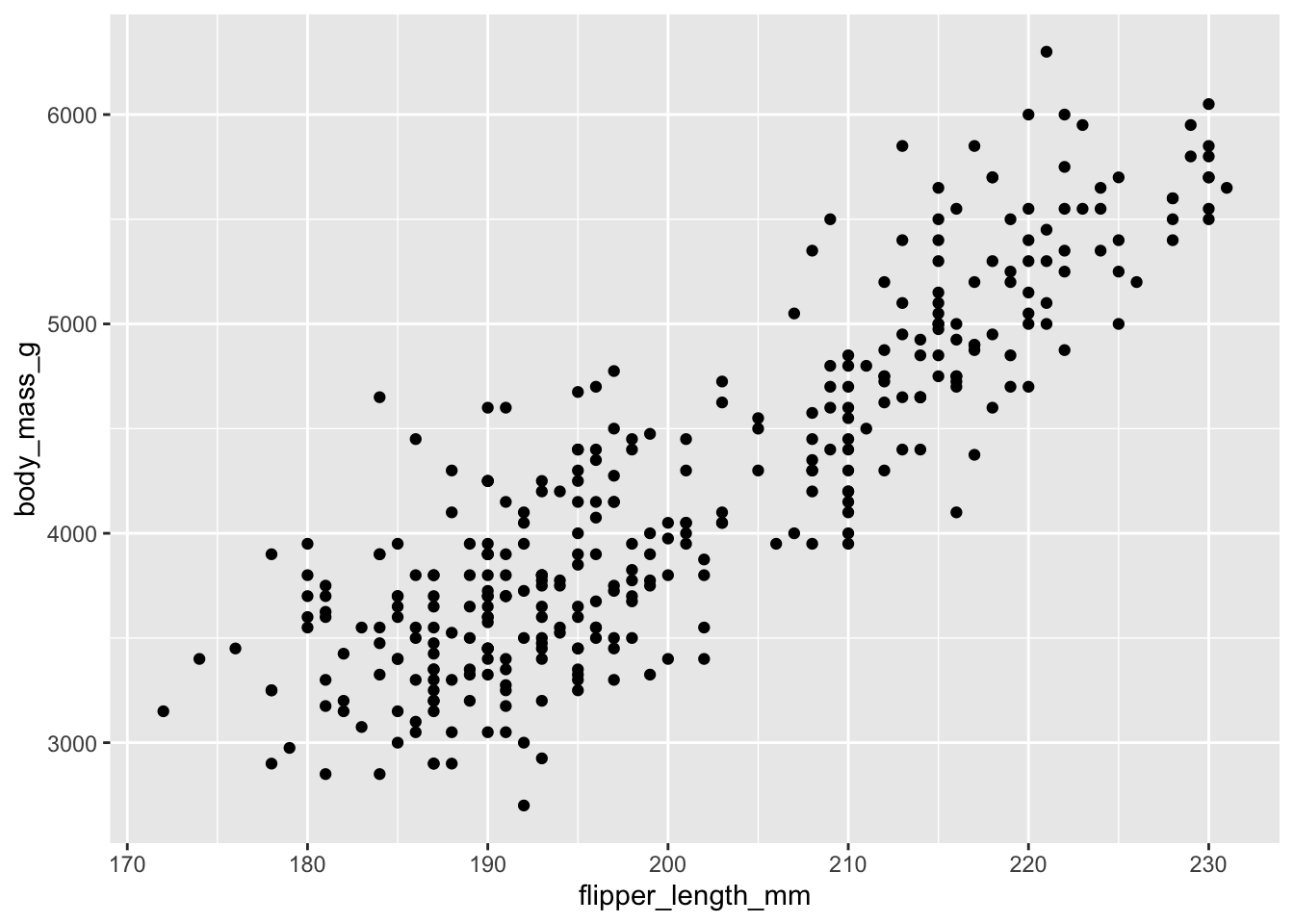

Correlation

Task 2 - Complete the following

Question: What is correlation? What values can correlation take?

Strength and direction of a linear relationship. It’s bounded by -1 and 1.

Note

Are you good at guessing correlation? Give it a try with this game!
Code: What is the correlation between flipper length and body mass of penguins?

# option 1
penguins |>
  summarize(r = cor(flipper_length_mm, body_mass_g, use = "complete.obs"))

# A tibble: 1 × 1
      r
  <dbl>
1 0.871

# option 2
penguins |>
  drop_na(flipper_length_mm, body_mass_g) |>
  summarize(r = cor(flipper_length_mm, body_mass_g))

# A tibble: 1 × 1
      r
  <dbl>
1 0.871

Defining, fitting, and summarizing a model

Task 3 (Demo) : Write the population model (model for the true values) below that explains the relationship between body mass and flipper length.

\[ {body mass} = \beta_0 + \beta_1 \times flipper length + \epsilon \]Task 4: Fit the linear regression model and display the results. Write the estimated model output below!

bm_fl_fit <- linear_reg() |>
  fit(body_mass_g ~ flipper_length_mm, data = penguins)

tidy(bm_fl_fit)

# A tibble: 2 × 5
  term              estimate std.error statistic   p.value
  <chr>                <dbl>     <dbl>     <dbl>     <dbl>
1 (Intercept)        -5781.     306.       -18.9 5.59e- 55
2 flipper_length_mm     49.7      1.52      32.7 4.37e-107

\[ \widehat{body mass} = -5780 + 49.7 \times flipper length \]

Task 5: Interpret the slope and the intercept in the context of the data.

Intercept: Penguins with 0 flipper length are expected, on average, to weigh -5,781 grams.
Slope: For each additional millimeter of a penguin;s flipper length, the weight of their penguin is expected to be higher, on average, by 49.7 grams.

Task 6: Recreate the visualization from above, this time adding a regression line to the visualization geom_smooth(method = "lm").

ggplot(
  penguins,
  aes(x = flipper_length_mm, y = body_mass_g)
  ) +
  geom_point() +
  geom_smooth(method = "lm")

`geom_smooth()` using formula = 'y ~ x'

Warning: Removed 2 rows containing non-finite outside the scale range
(`stat_smooth()`).

Warning: Removed 2 rows containing missing values or values outside the scale range
(`geom_point()`).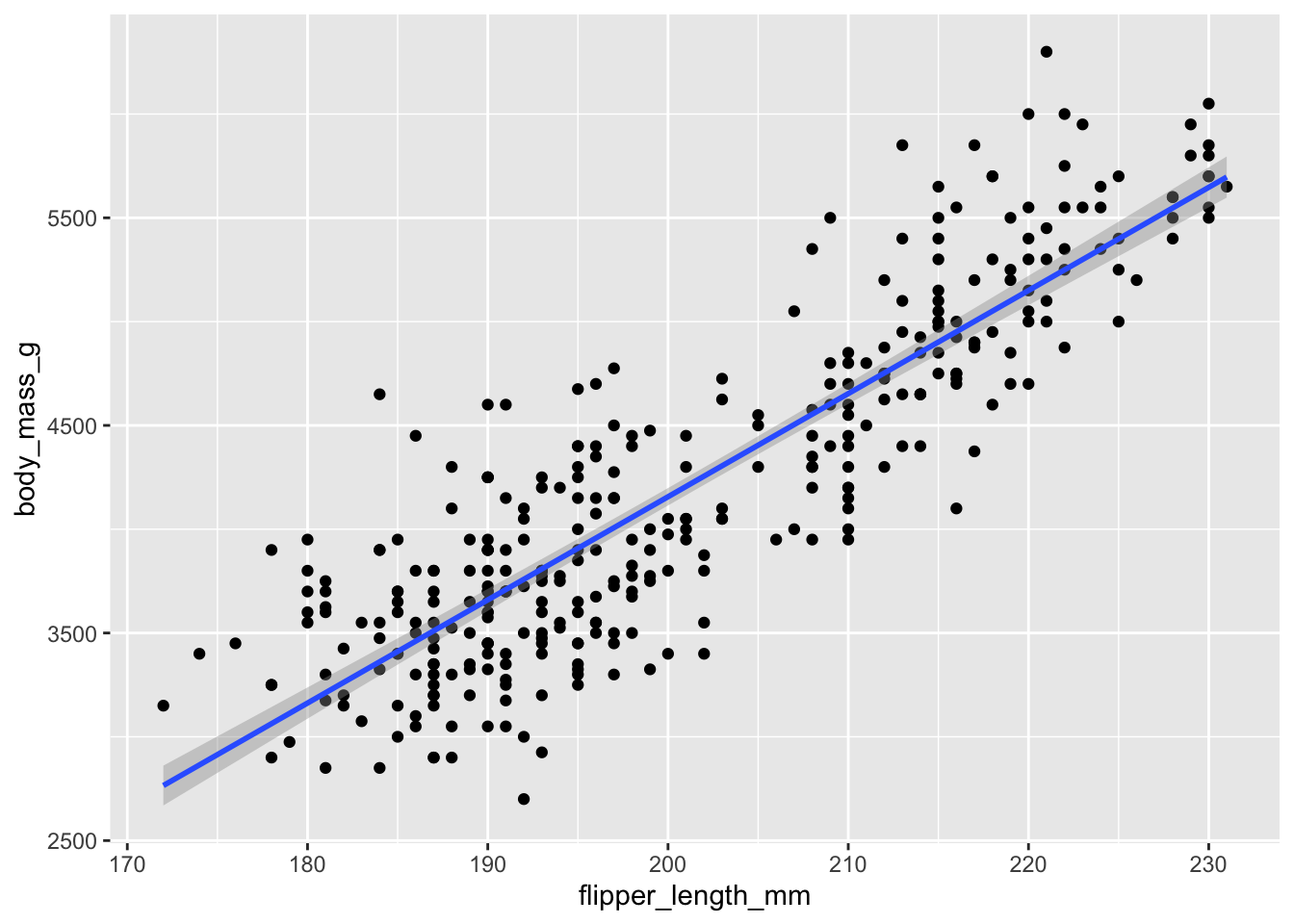

Task 7 (Demo): What is the estimated body mass for a penguin with a flipper length of 210?

penguin_flipper_210 <- tibble(flipper_length_mm = 210)

bm_fl_fit |>
  predict(new_data = penguin_flipper_210)

# A tibble: 1 × 1
  .pred
  <dbl>
1 4653.

Task 8: What is the estimated body mass for a penguin with a flipper length of 100? Add code to find it! Is there anything weird about making this prediction?

penguin_flipper_100 <- tibble(flipper_length_mm = 100)

bm_fl_fit |>
  predict(new_data = penguin_flipper_100)

# A tibble: 1 × 1
  .pred
  <dbl>
1 -812.

We are extrapolating when we take flipper length = 100: it is outside of the data range.

Part 2: Another model

Task 9: A different researcher wants to look at body weight of penguins based on the island they were recorded on.

Question: How are the variables involved in this analysis different?

The predictor variable is categorical, not quantitative!
Code: Make an appropriate visualization to investigate this relationship below. Additionally, calculate the mean body mass by island.

penguins |>
  ggplot(aes(x = island, y = body_mass_g)) +
  geom_boxplot()

Warning: Removed 2 rows containing non-finite outside the scale range
(`stat_boxplot()`).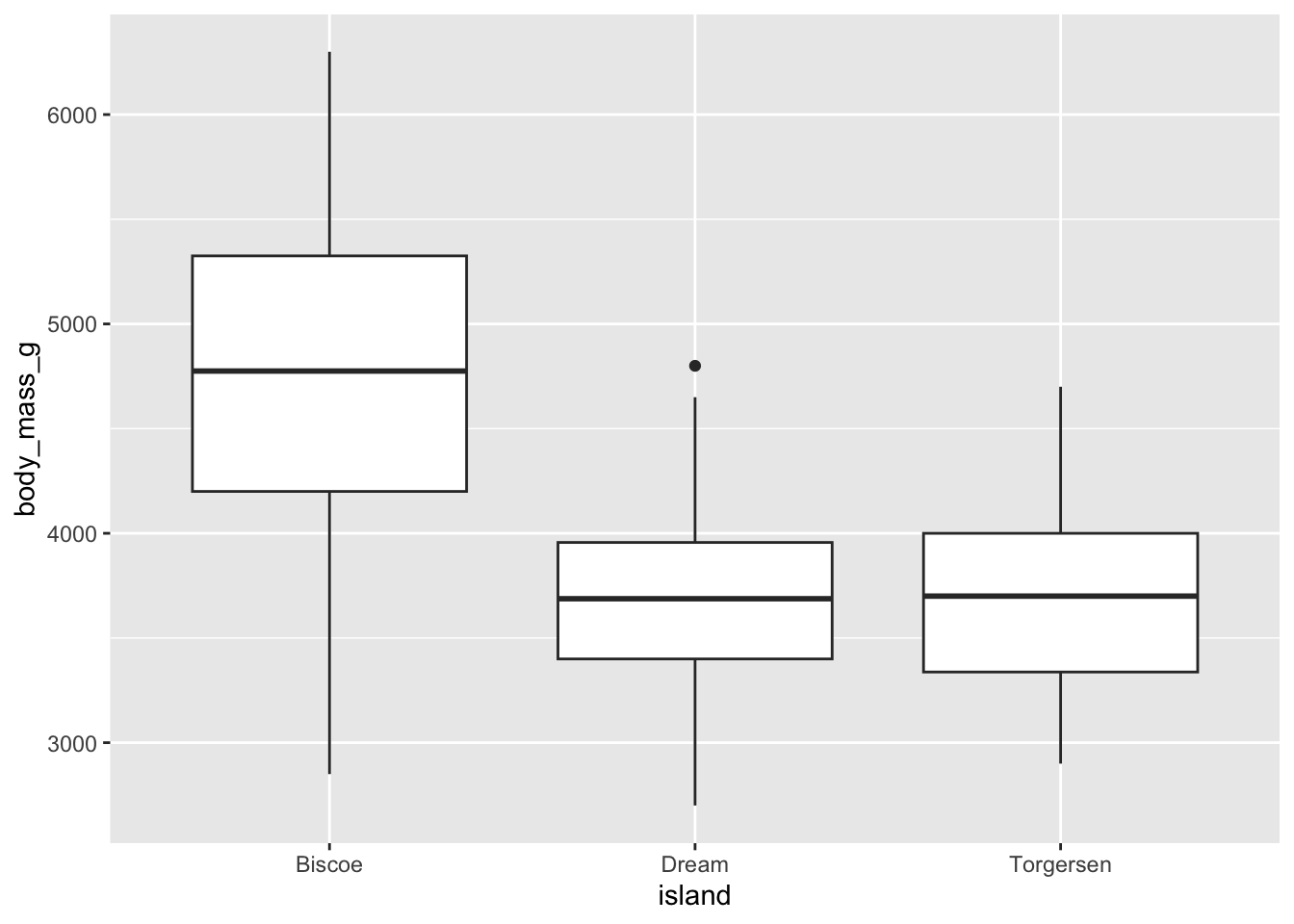

penguins |>
  group_by(island) |>
  summarize(mean_bm = mean(body_mass_g, na.rm = TRUE))

# A tibble: 3 × 2
  island    mean_bm
  <fct>       <dbl>
1 Biscoe      4716.
2 Dream       3713.
3 Torgersen   3706.

Task 10: Change the geom of your previous plot to geom_point(). Use this plot to think about how R models these data.

penguins |>
  ggplot(aes(x = island, y = body_mass_g)) +
  geom_point()

Warning: Removed 2 rows containing missing values or values outside the scale range
(`geom_point()`).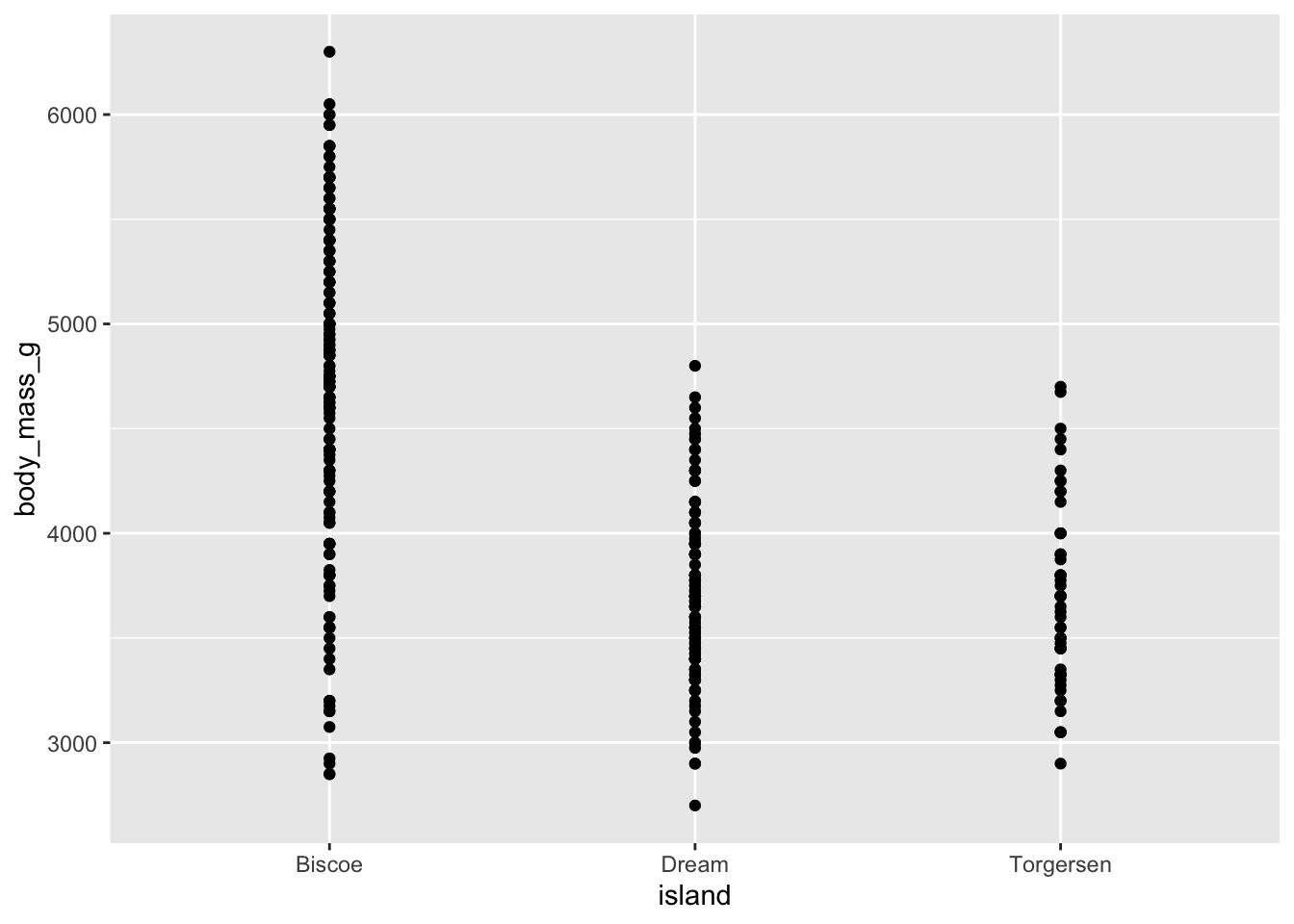

Task 11: Fit the linear regression model and display the results. Write the estimated model output below.

bm_island_fit <- linear_reg() |>
  fit(body_mass_g ~ island, data = penguins)

tidy(bm_island_fit)

# A tibble: 3 × 5
  term            estimate std.error statistic   p.value
  <chr>              <dbl>     <dbl>     <dbl>     <dbl>
1 (Intercept)        4716.      48.5      97.3 8.93e-250
2 islandDream       -1003.      74.2     -13.5 1.42e- 33
3 islandTorgersen   -1010.     100.      -10.1 4.66e- 21

\[ \widehat{bodymass} = 4716 -1003 \times dream -1010 \times torgersen \]

Interpreting Categorical Predictors

Task 12: Fill in the blanks.

The baseline island is Biscoe.
Intercept: Penguins from Biscoe island are expected to weigh, on average, 4716 grams.
Slopes:
- Penguins from Dream are expected to weigh, on average, 1003 grams less than those from Biscoe.
- Penguins from Torgersen island are expected to weigh, on average, 1010 grams less than those from Biscoe.

Task 13: What is the estimated body weight of a penguin on Biscoe island? What are the estimated body weights of penguins on Dream and Torgersen islands?

three_penguins <- tibble(
  island = c("Biscoe", "Dream", "Torgersen")
)

bm_island_fit |>
  predict(new_data = three_penguins)

# A tibble: 3 × 1
  .pred
  <dbl>
1 4716.
2 3713.
3 3706.