Quantifying uncertainty with bootstrap intervals

Lecture 20

June 12, 2025

Announcements

Project timeline and progress:

• Due TONIGHT: Milestone 3
  • Address and close issues (let me know if you are having trouble closing!)
  • At least one plot
  • All team members commit
• Before Monday - Between Milestones 3 and 4
  • Make real progress on your project write-up: introduction and exploratory data analysis; brainstorm of methods you plan to use
  • Ideal: Start trying the methods!
• On Monday - Milestone 4
  • First 30 mins: talk/work as teams
  • Last 45 mins: give feedback to another team!

Yesterday was a lot…

Quick Recap!

Confusion Matrix

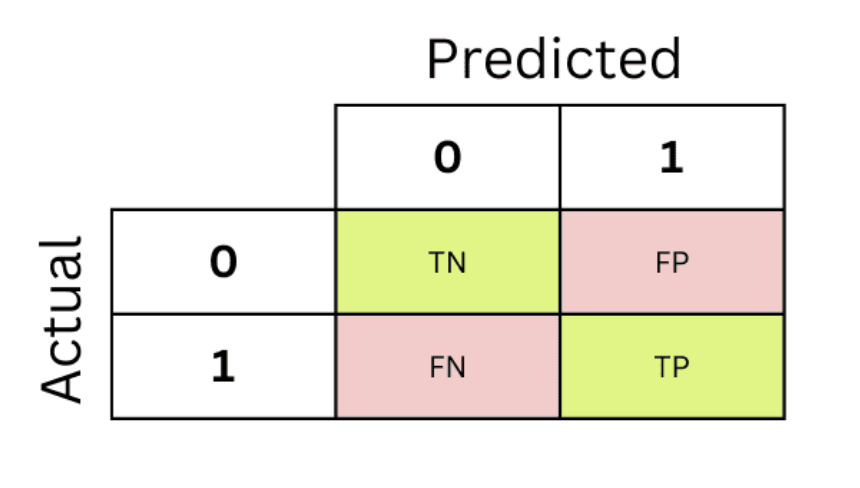
• False negative rate = \(\frac{FN}{FN + TP}\)
• False positive rate = \(\frac{FP}{FP + TN}\)
• Sensitivity = \(\frac{FN}{FN + TP}\) = 1 − False negative rate
• Specificity = \(\frac{TN}{FP + TN}\) = 1 - False positive rate

ROC Curve

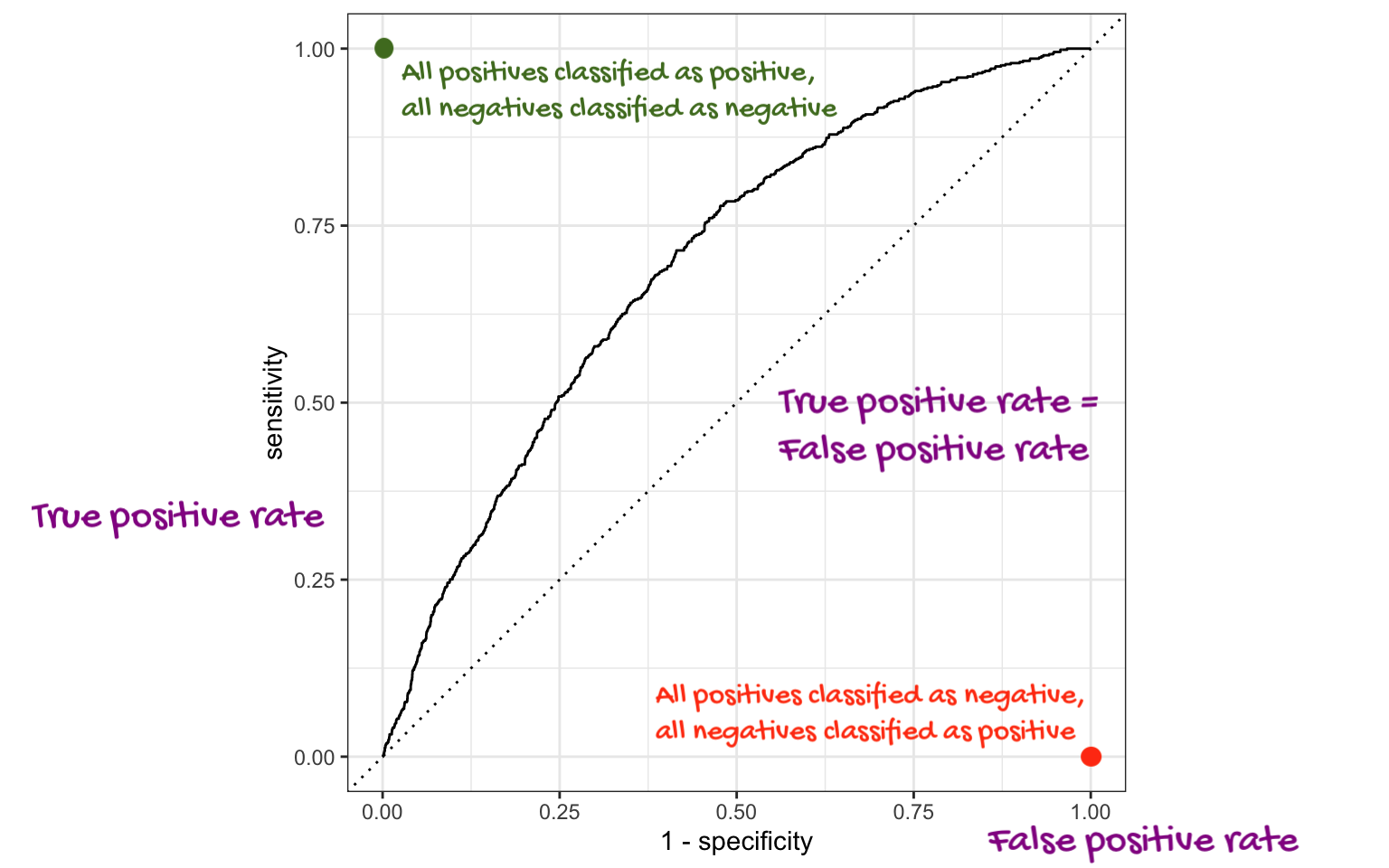
Quantifying uncertainty

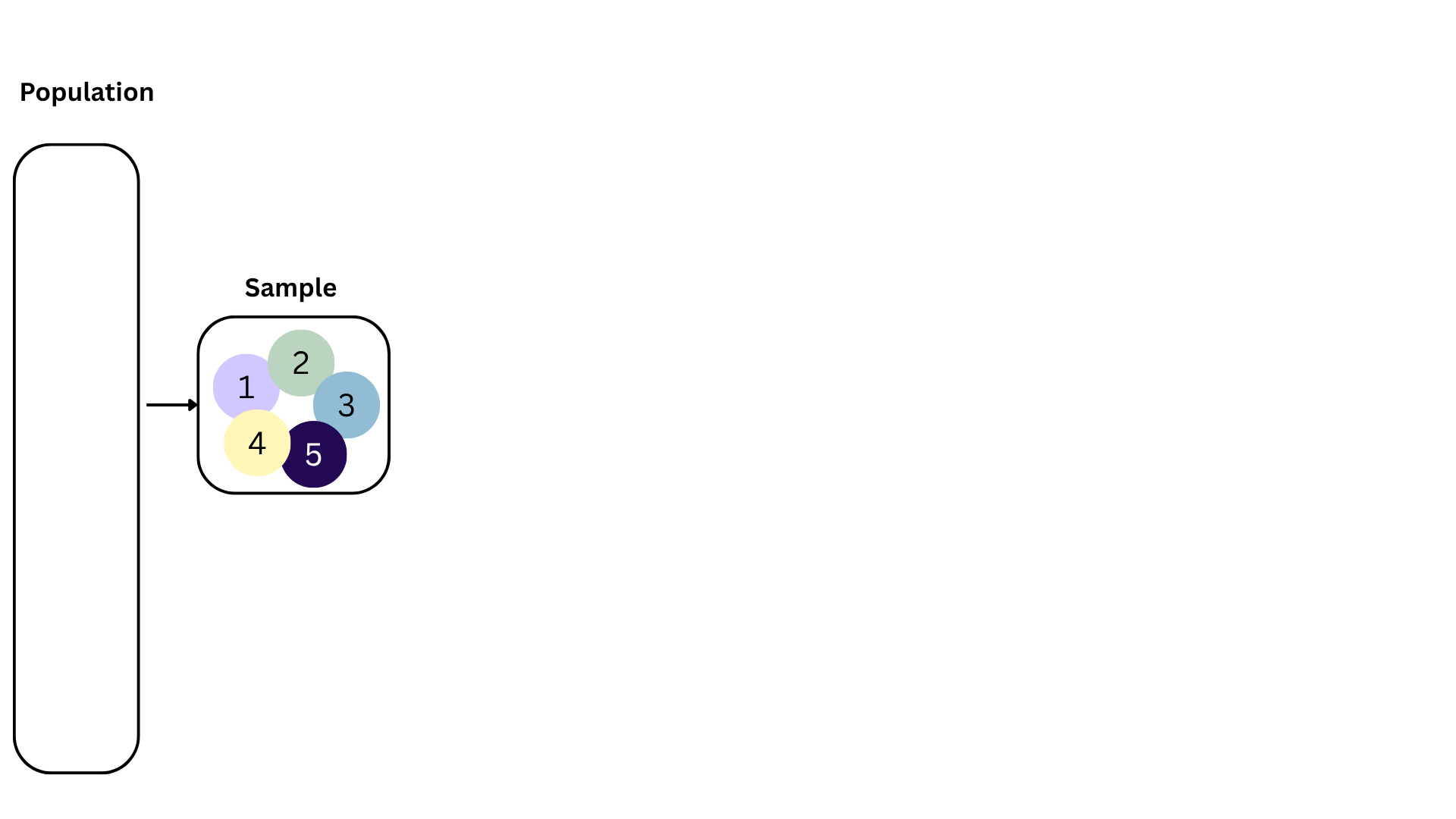
Samples

Generally, we don’t have information about an entire population, we have data for a sample:

• Election polling: we can’t ask everybody who they are voting for

• Housing data: we don’t have a data set with every single house

• Medical research: we don’t test a new drug on everyone, just on a sample of patients in a clinical trial.

• Ecology studies: scientists might analyze a smaller sample of animals/plants

There is uncertainty about true population parameters.

Statistical inference

• Statistical inference provide methods and tools so we can use the single observed sample to make valid statements (inferences) about the population it comes from

• For our inferences to be valid, the sample should be random and representative of the population we’re interested in

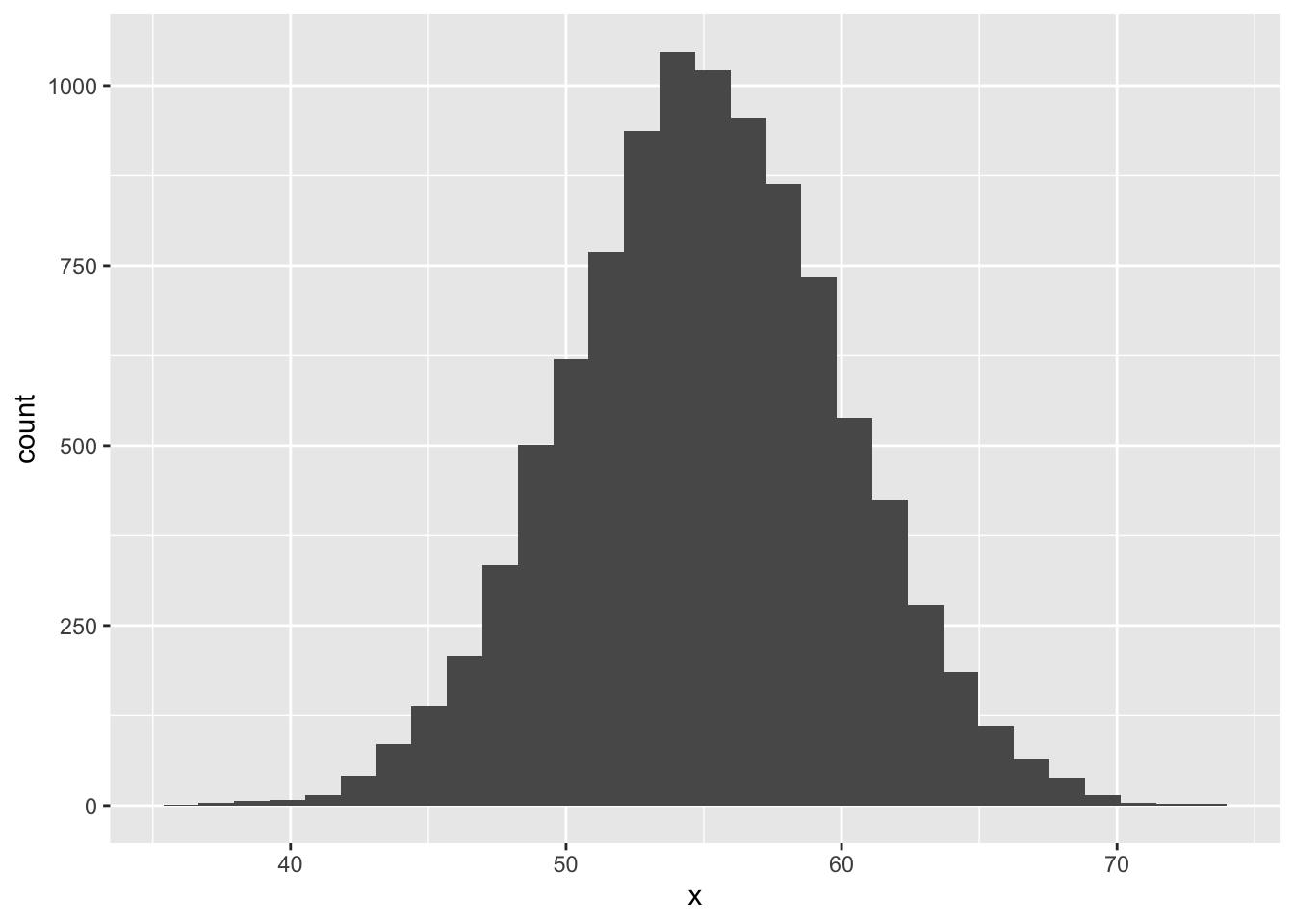
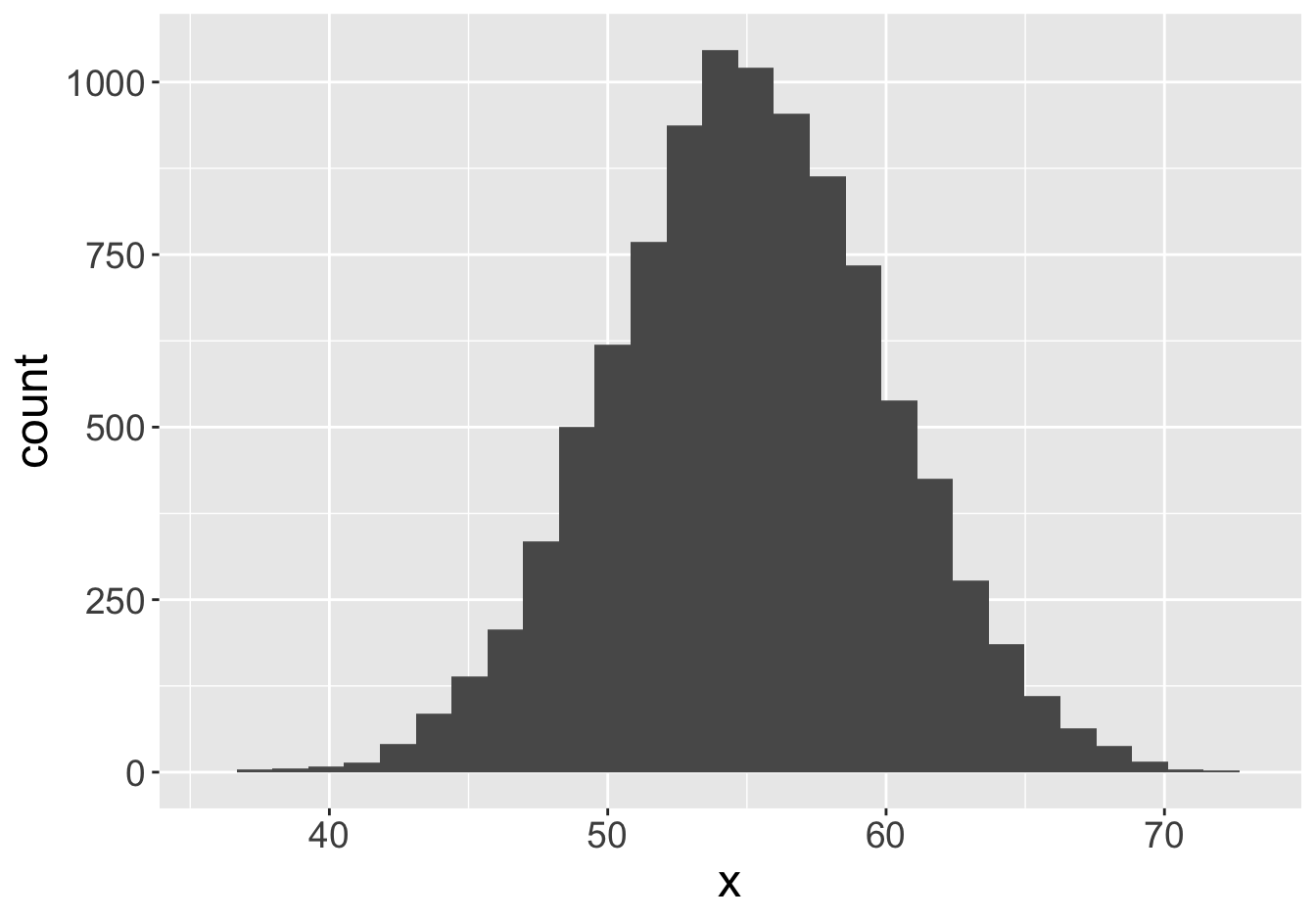
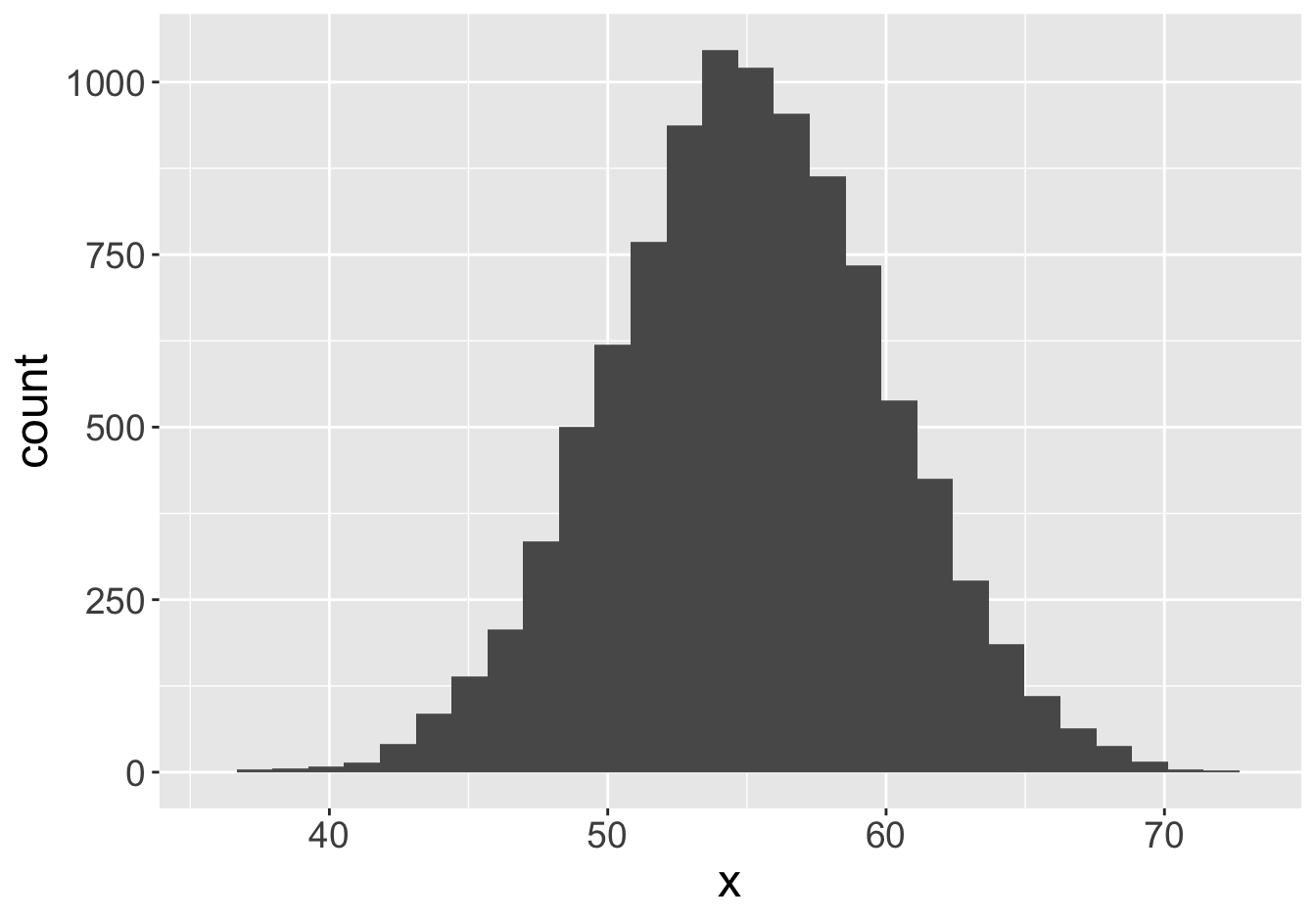
Example - Means

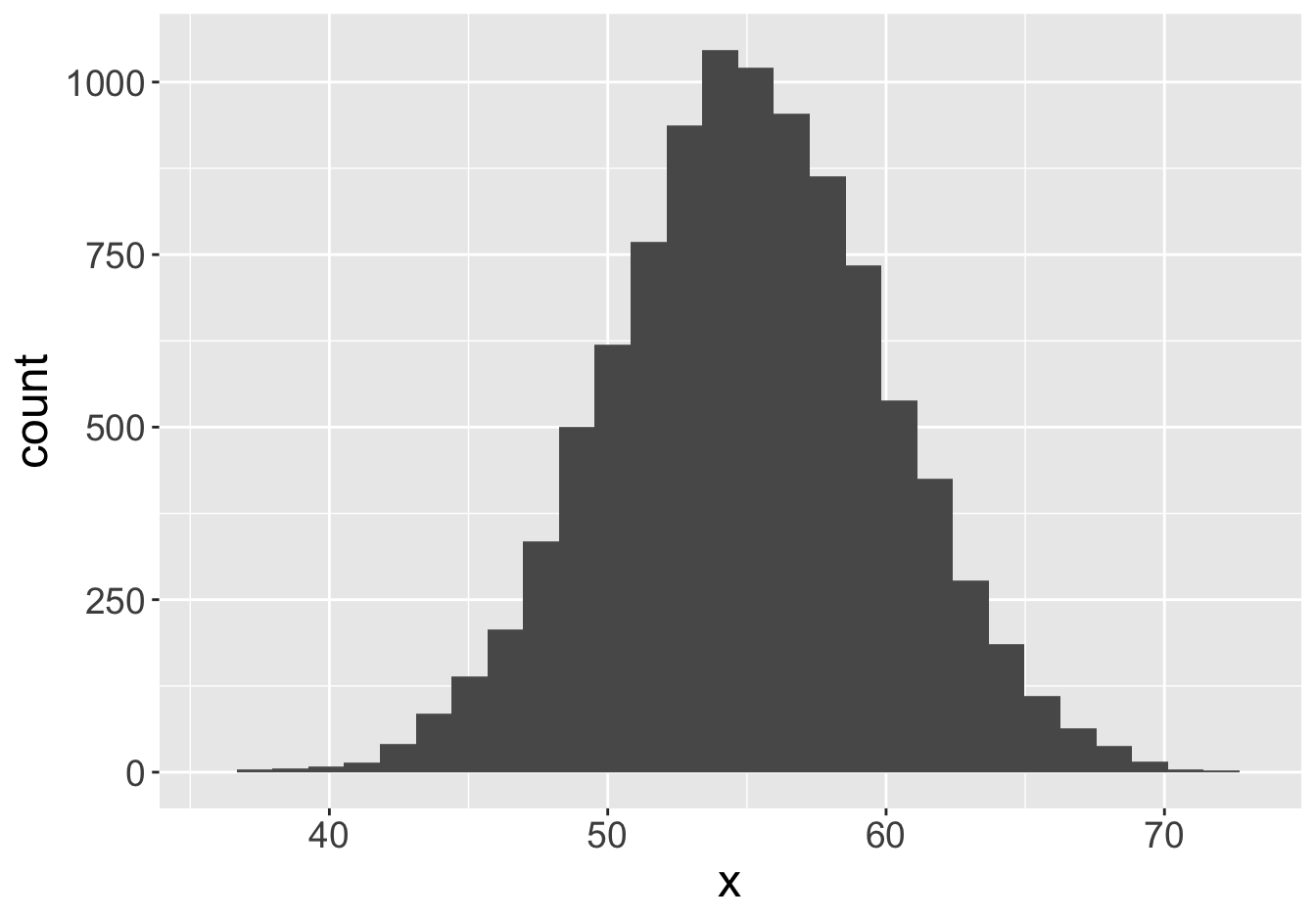
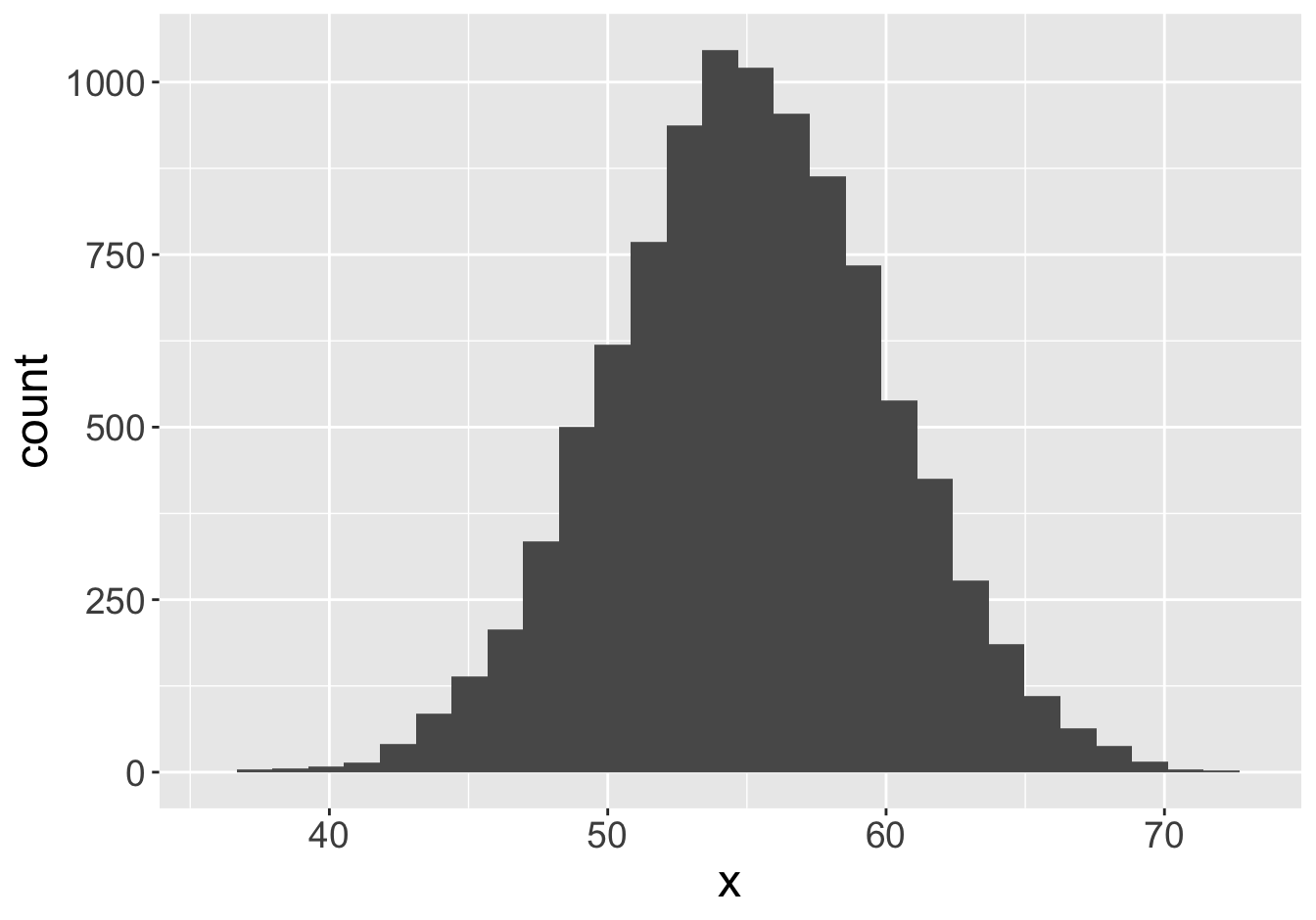
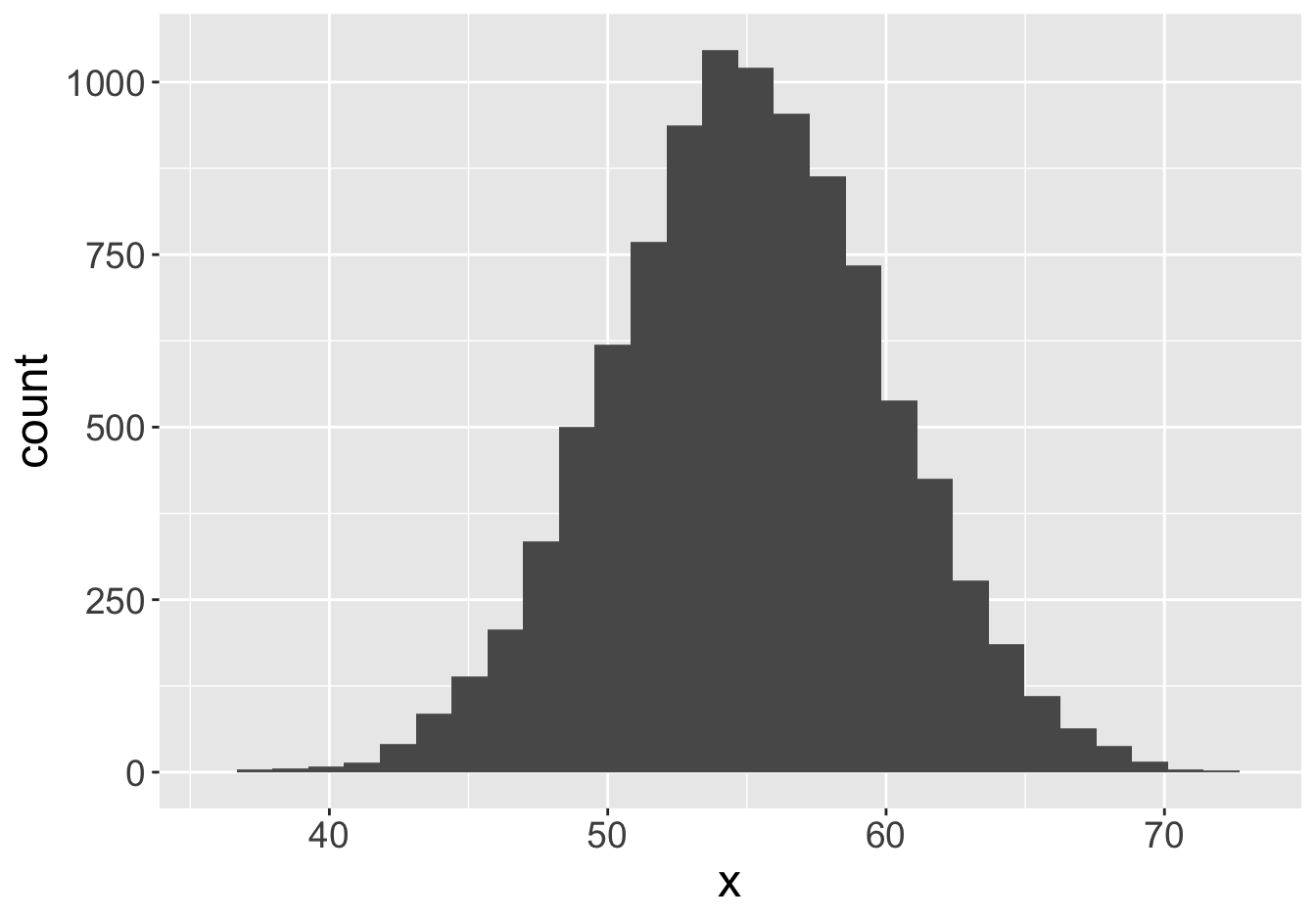
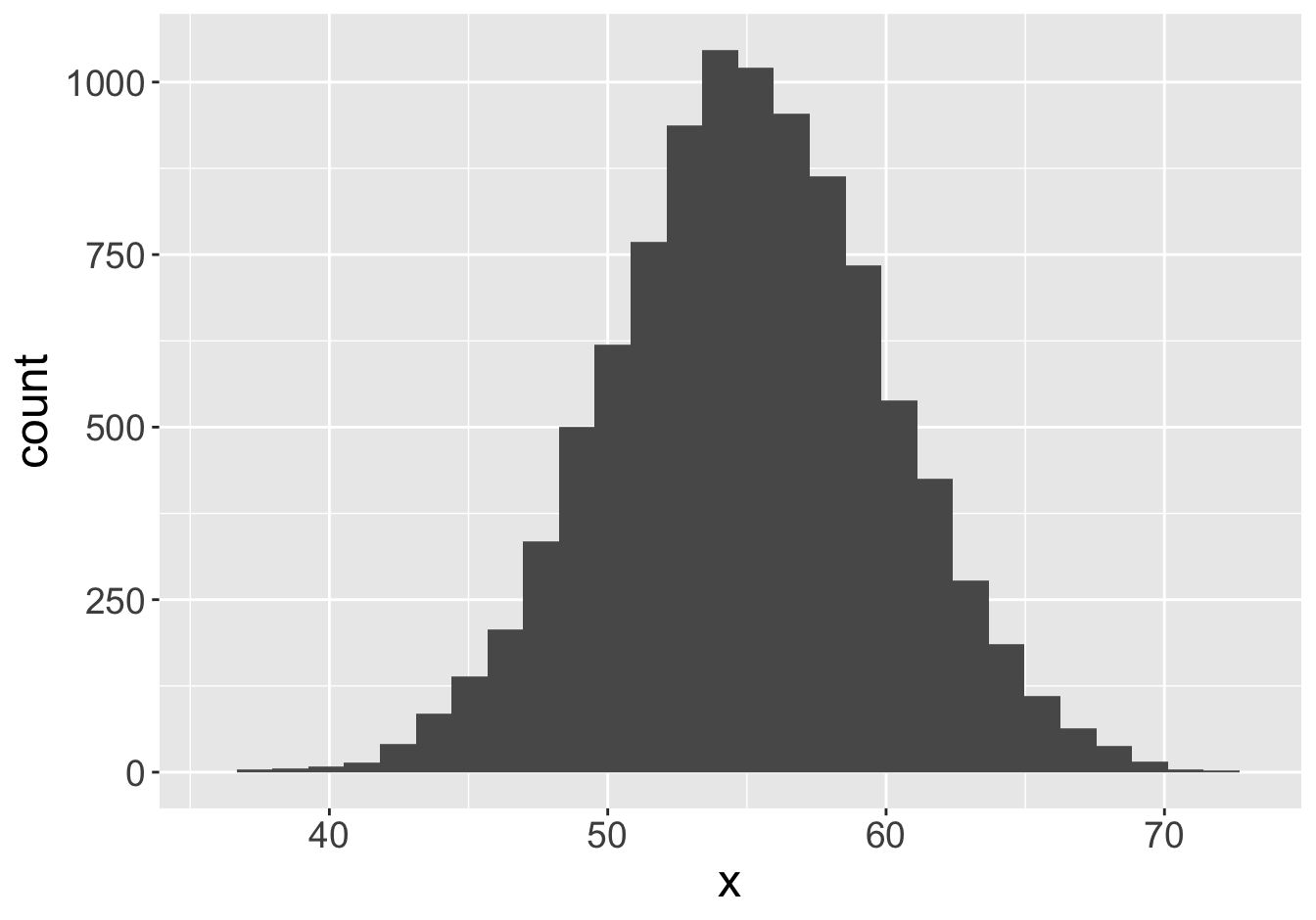
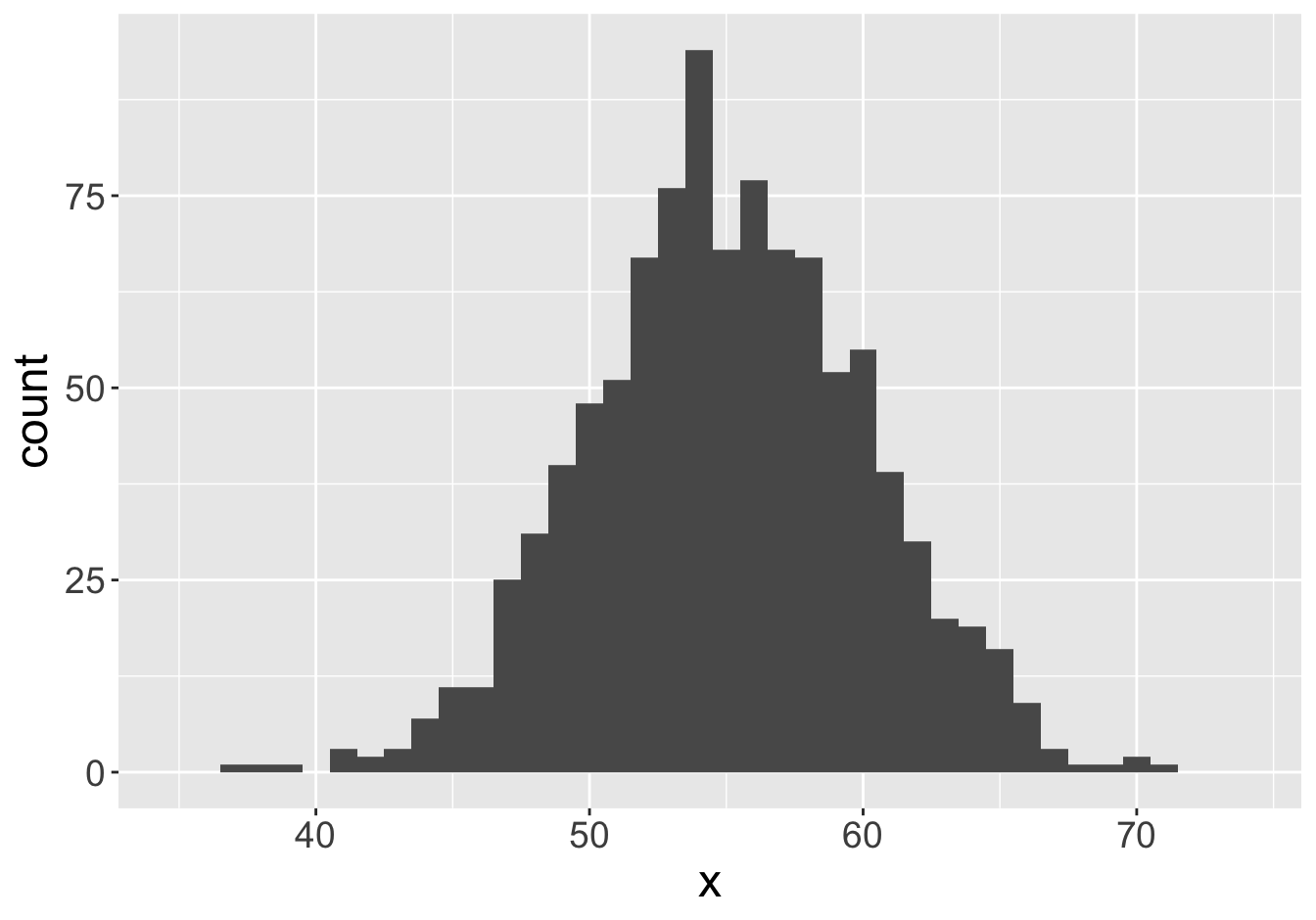
Suppose this histogram represents some value \(x\) in a population of 10,000:

Mean: 55.06

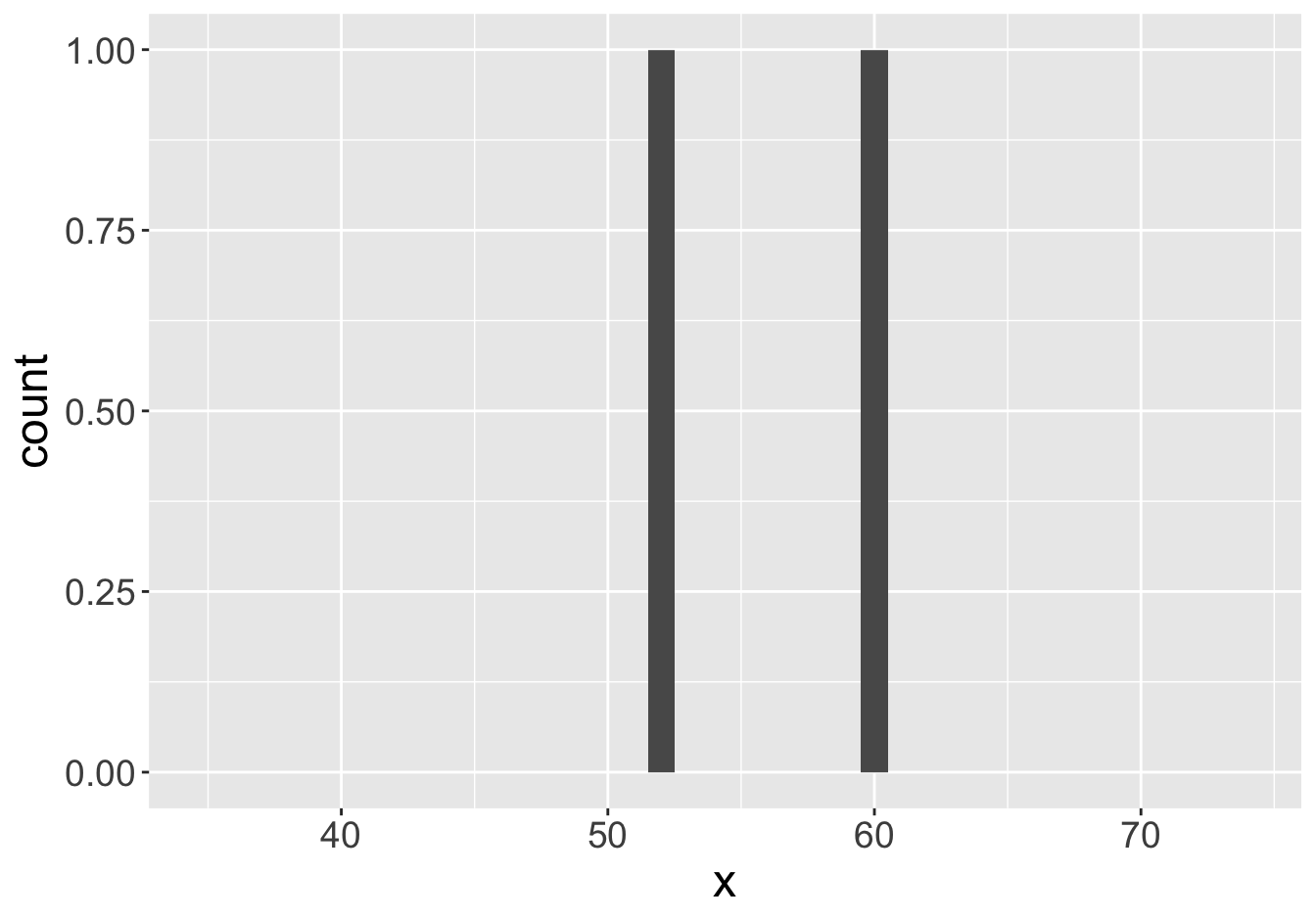
Example - Means (Sample Size 2)

Mean: 55.06

Mean: 55.9

Example - Means (Sample Size 2)

Mean: 55.06

Mean: 47.8

Example - Means (Sample Size 2)

Mean: 55.06

Mean: 56.08

Example - Means (Sample Size 2)

Mean: 55.06

Mean: 54.38

Example - Means (Sample Size 2)

Mean: 55.06

Mean: 59.24

Example - Means (Sample Size 10)

Mean: 55.06

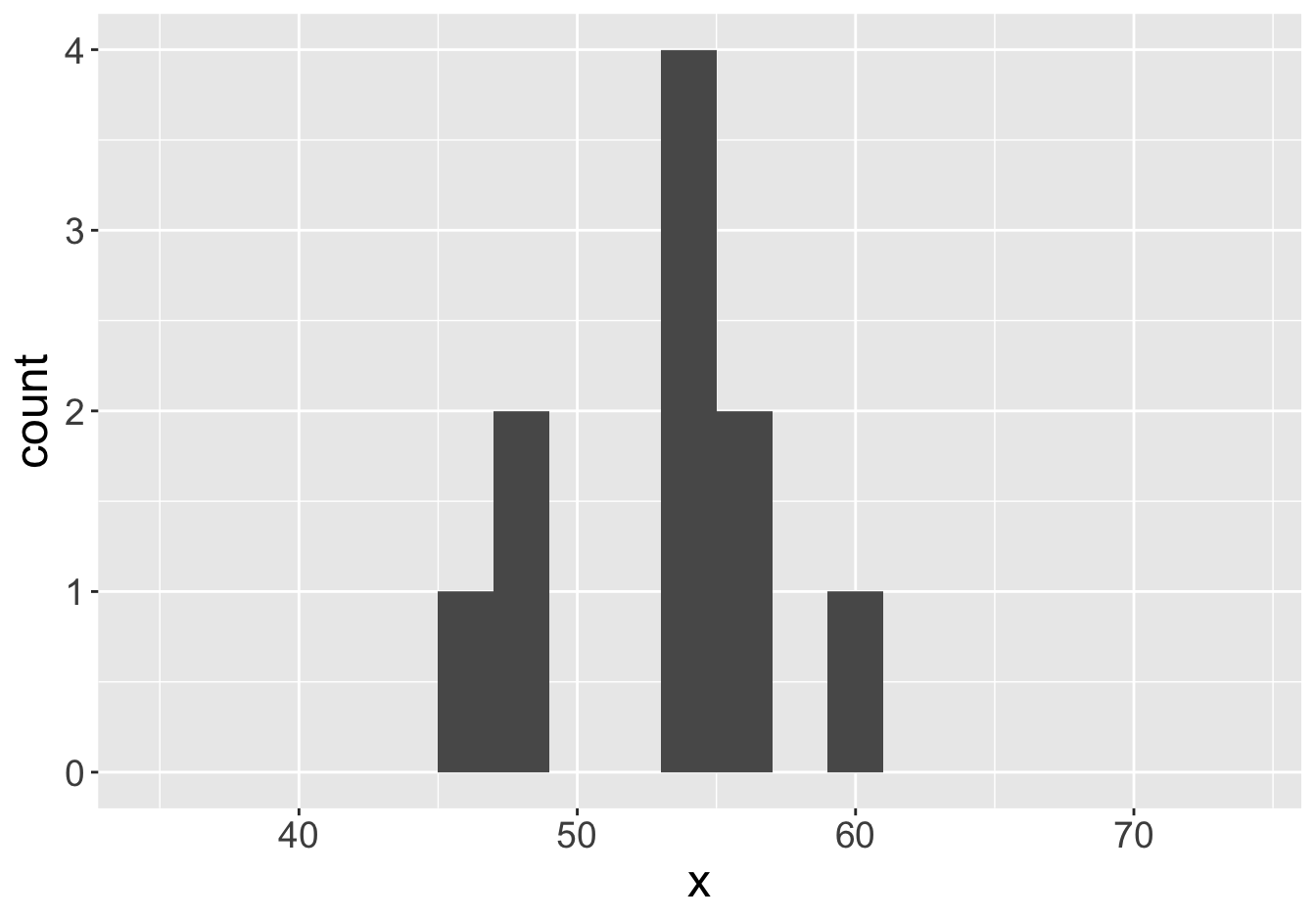
Mean: 53.29

Example - Means (Sample Size 10)

Mean: 55.06

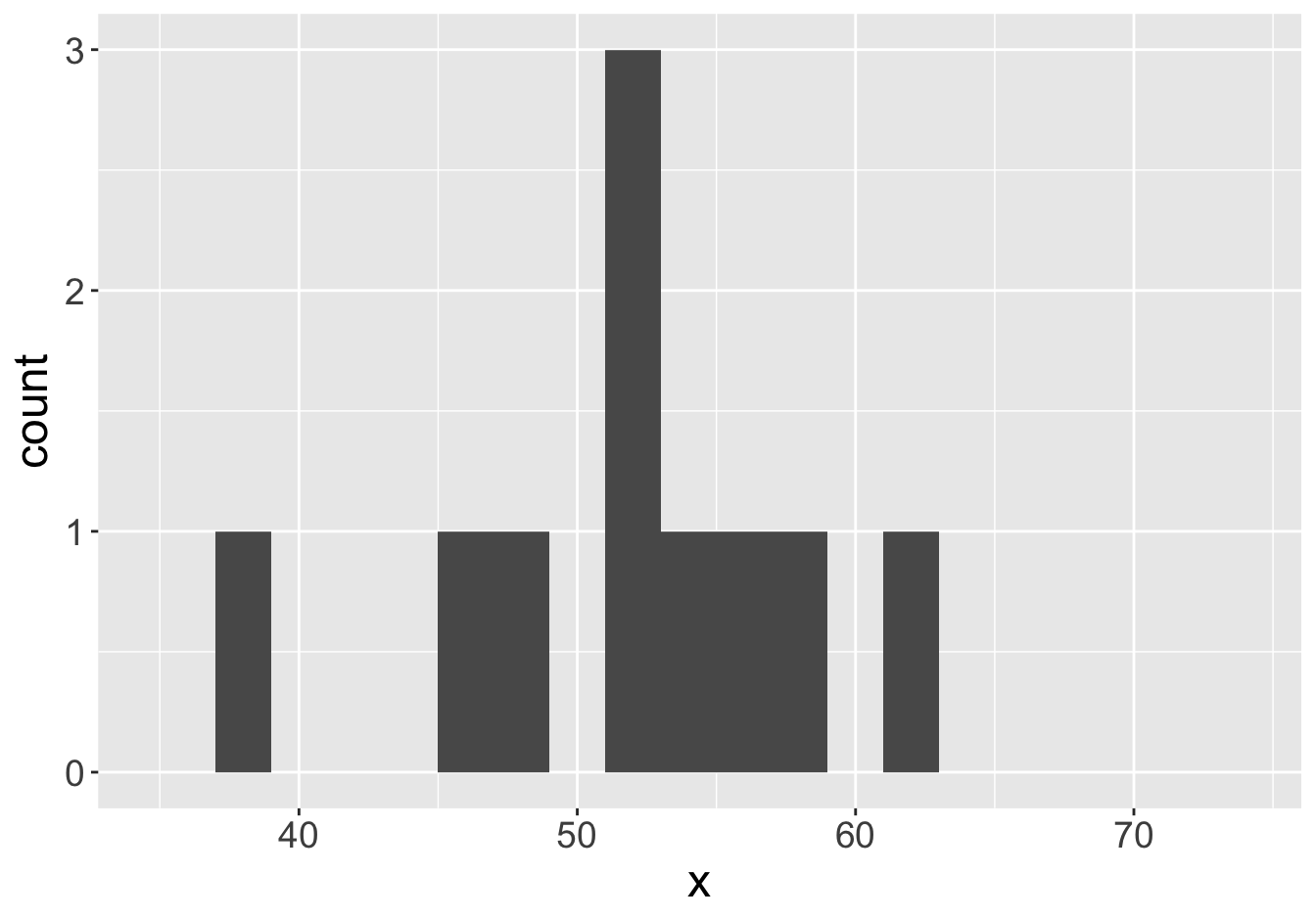
Mean: 51.59

Example - Means (Sample Size 10)

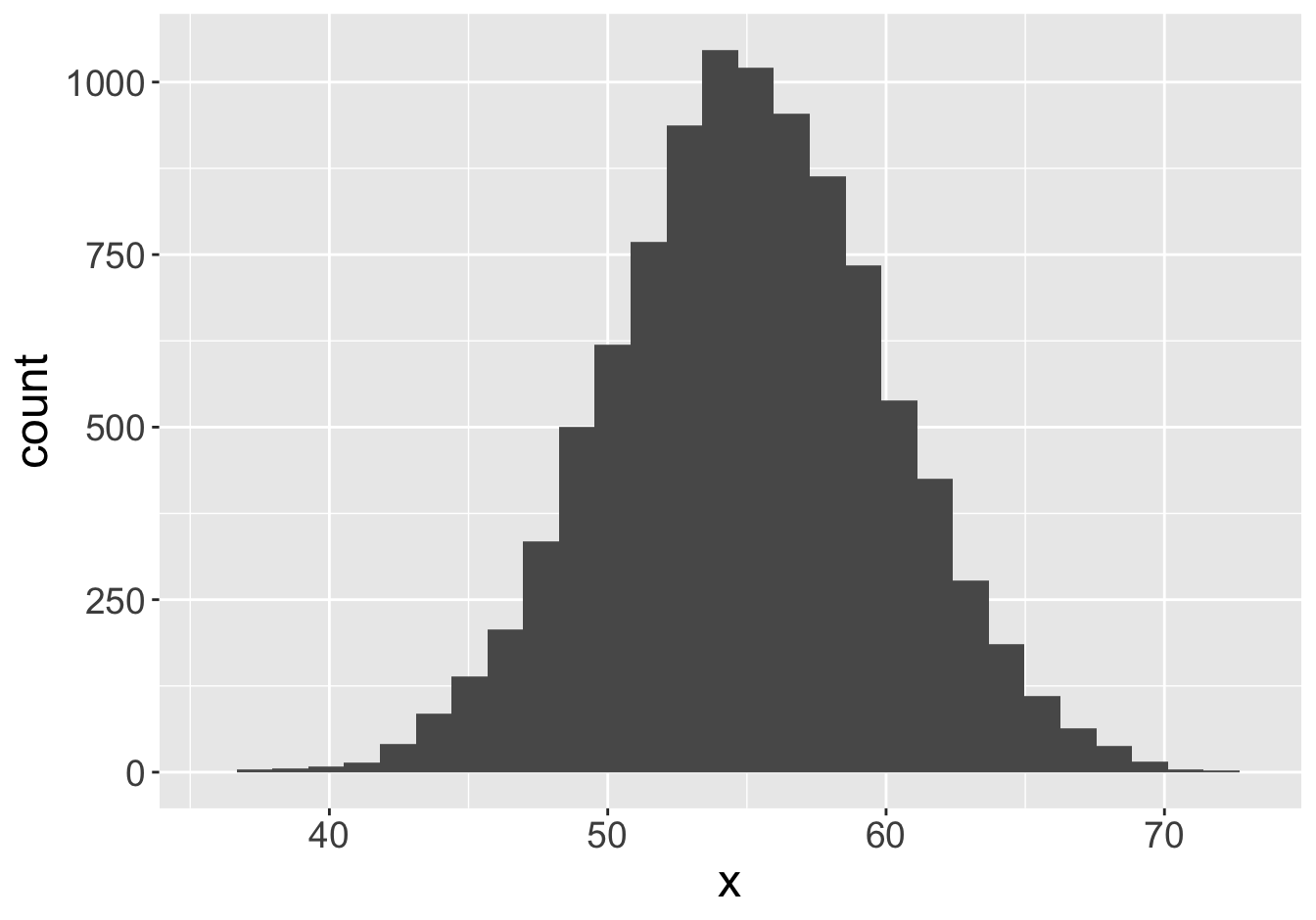
Mean: 55.06

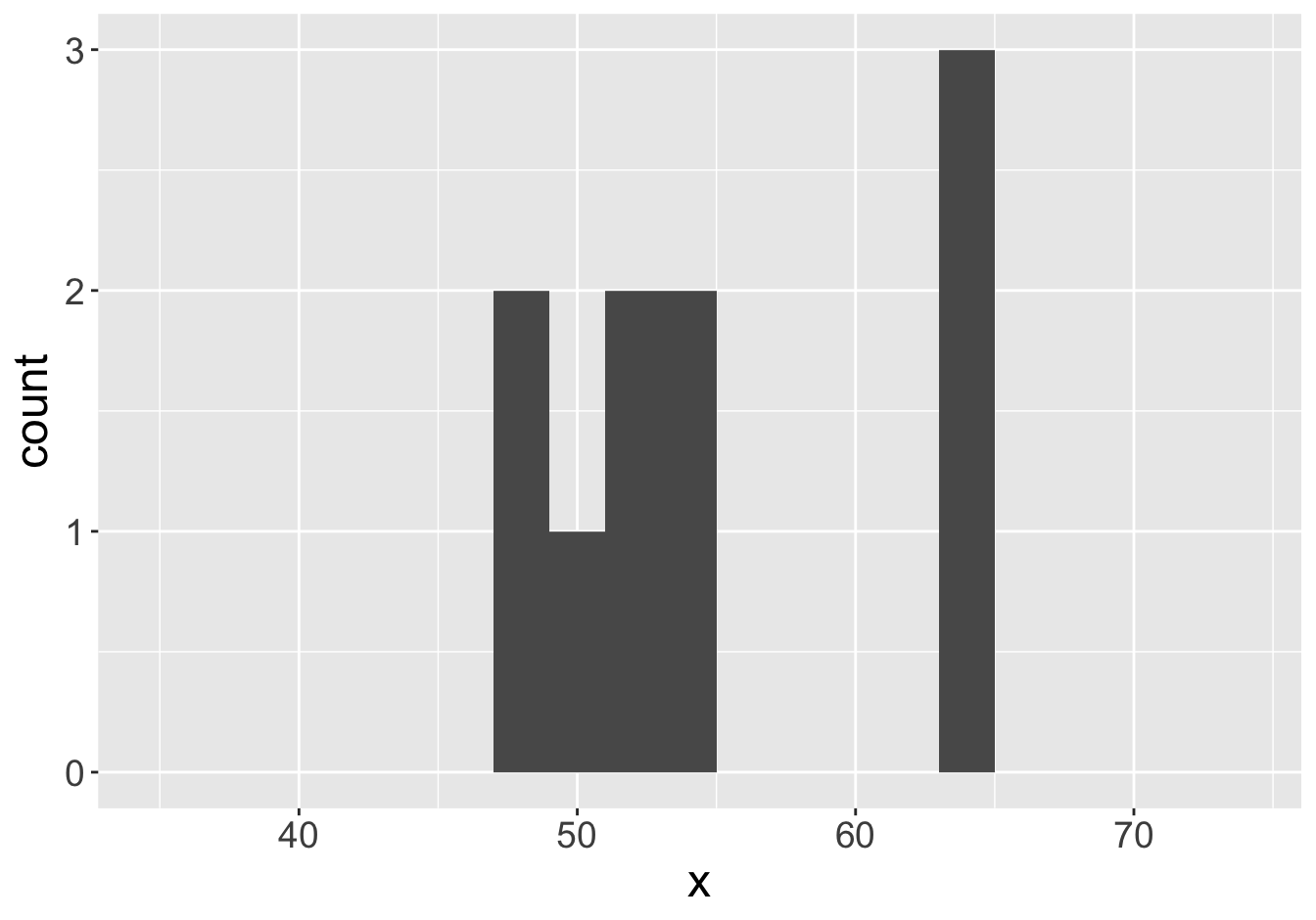
Mean: 55.24

Example - Means (Sample Size 10)

Mean: 55.06

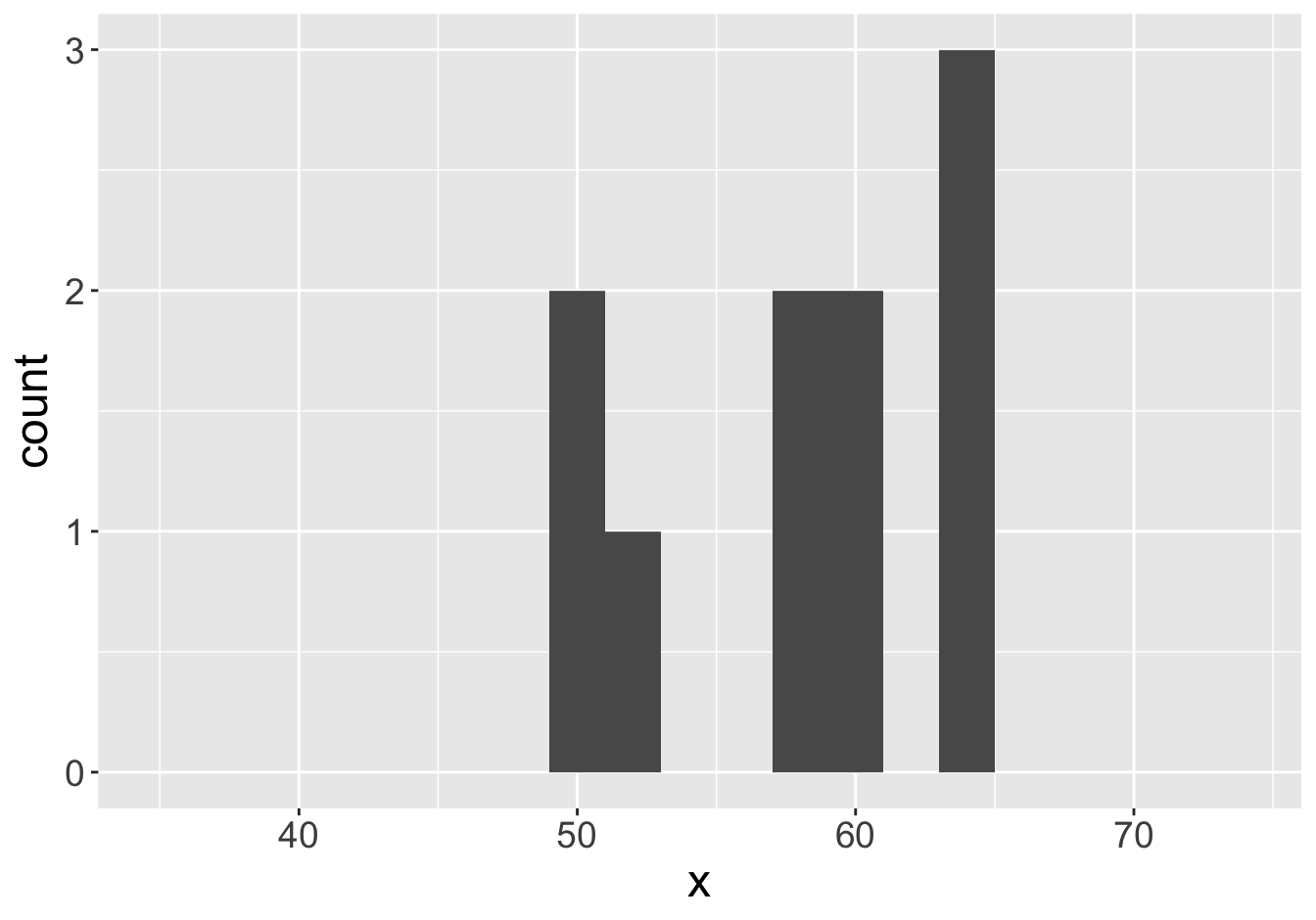
Mean: 57.99

Example - Means (Sample Size 10)

Mean: 55.06

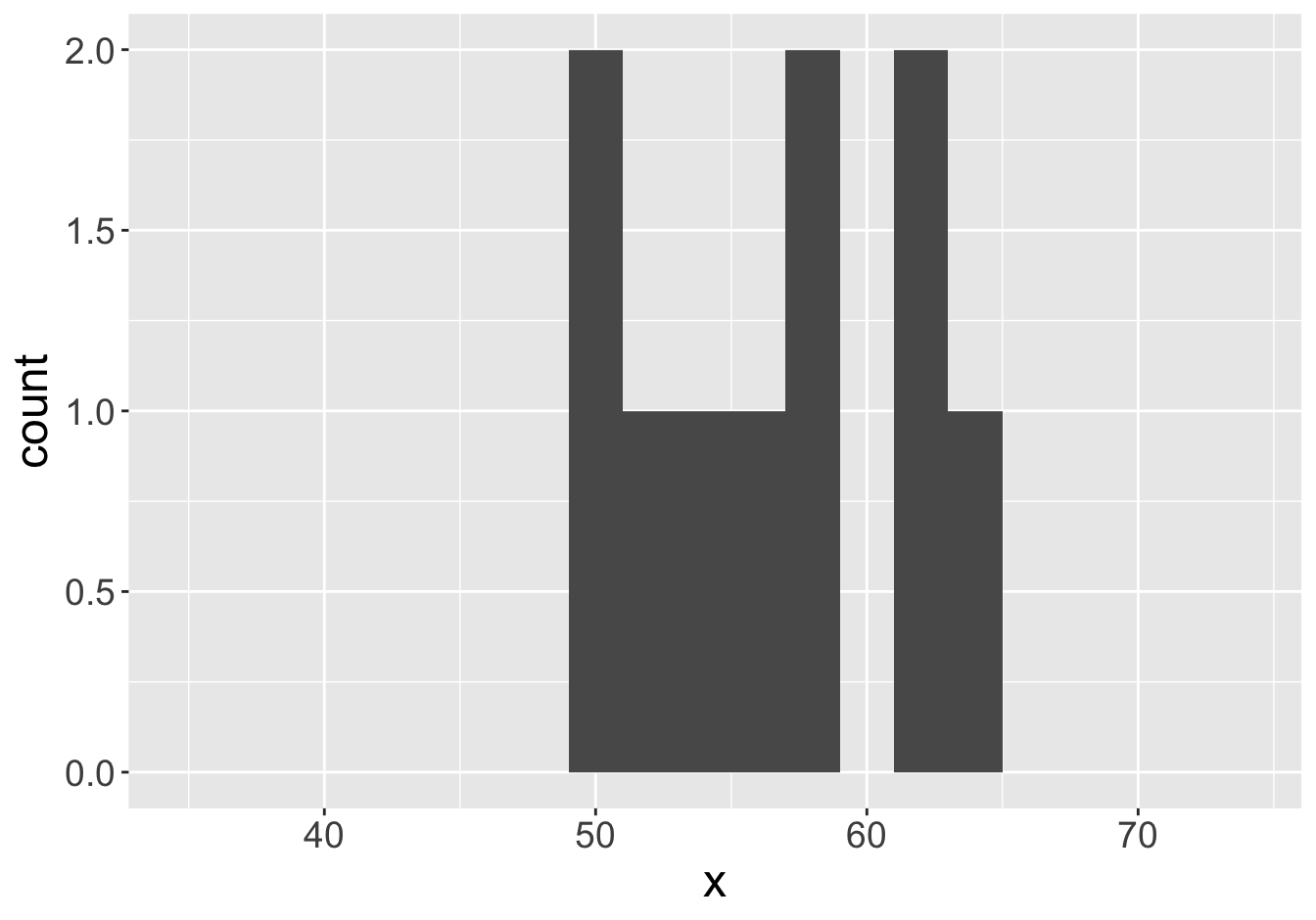
Mean: 56.54

Example - Means (Sample Size 100)

Mean: 55.06

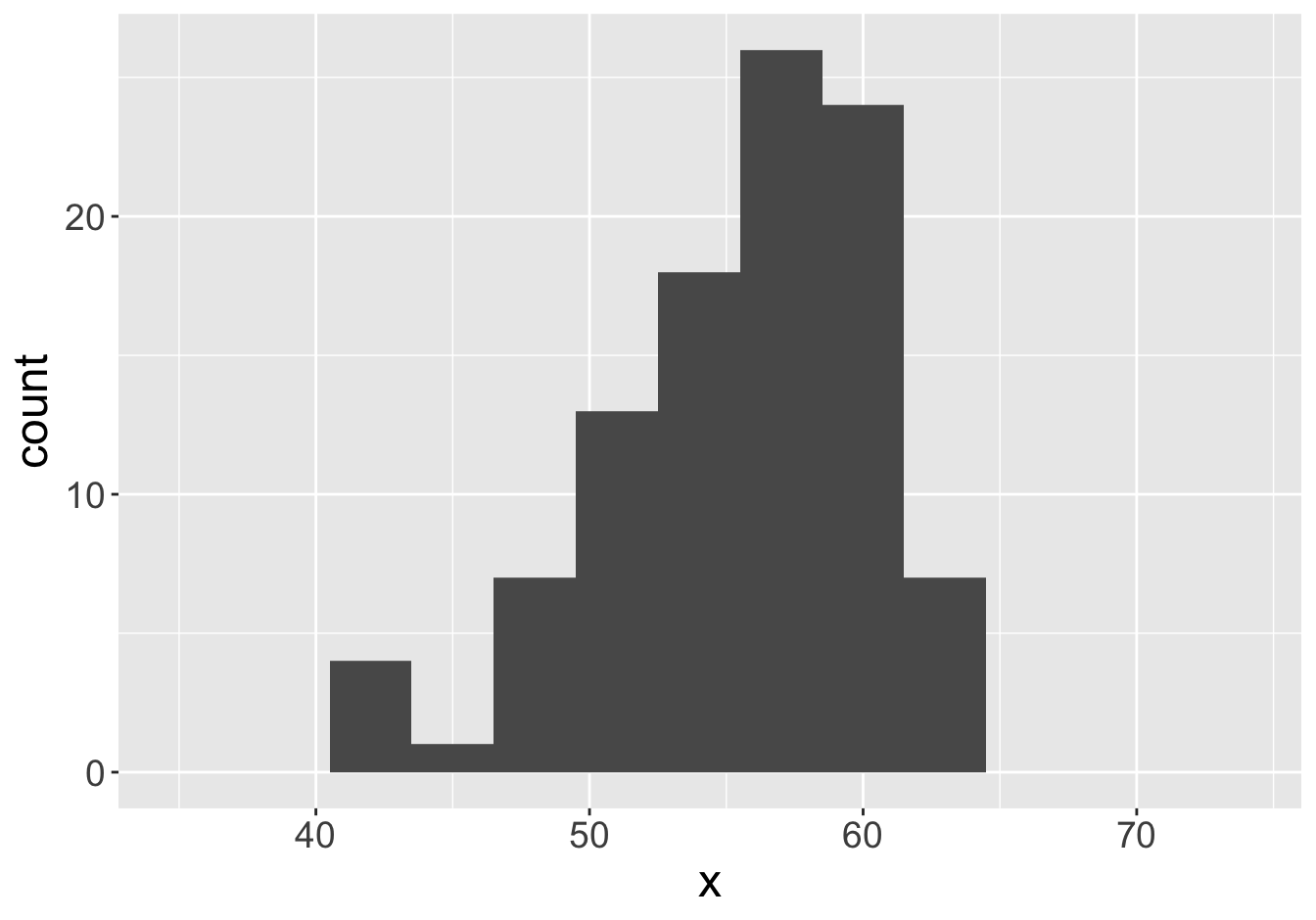
Mean: 55.55

Example - Means (Sample Size 100)

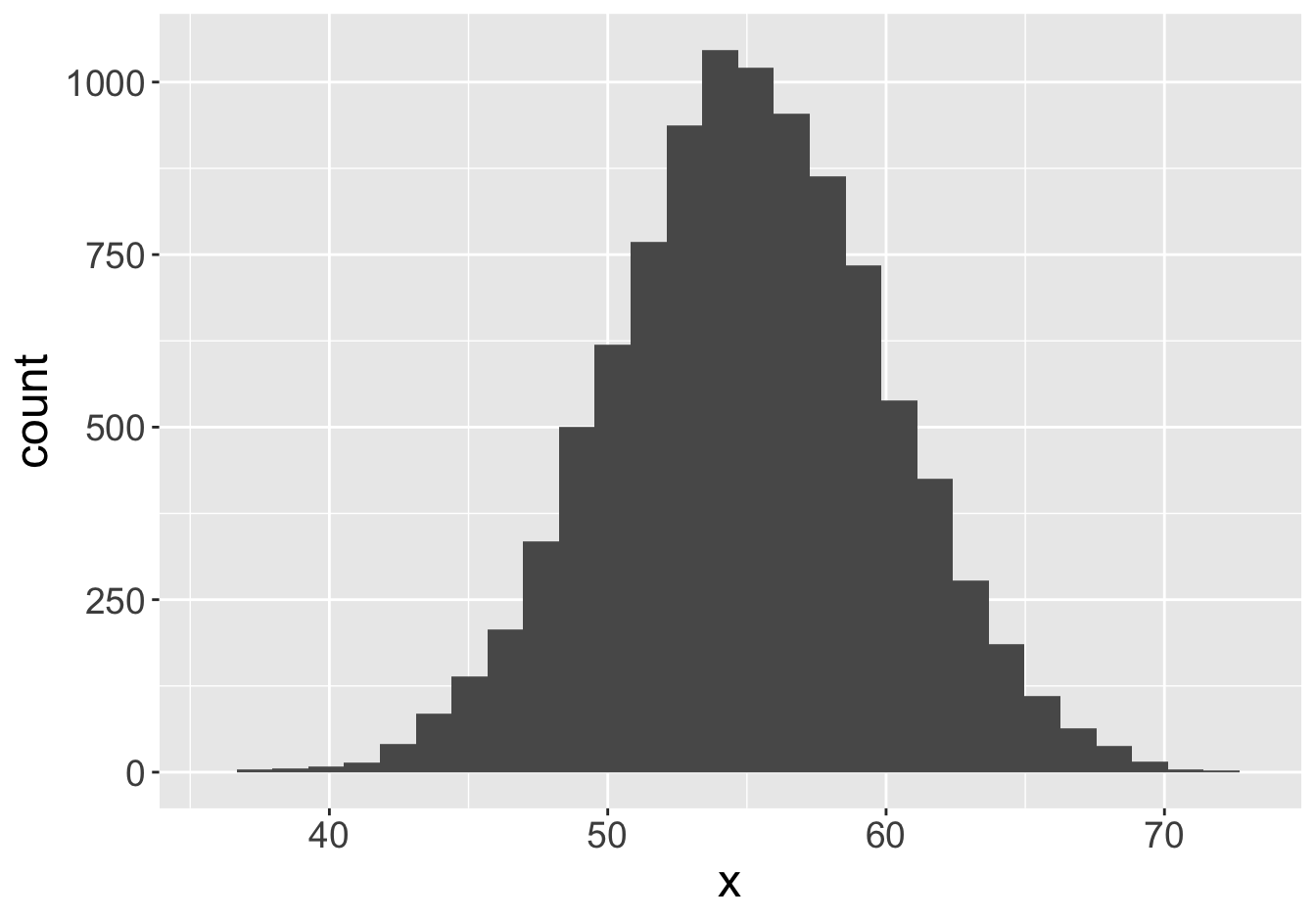
Mean: 55.06

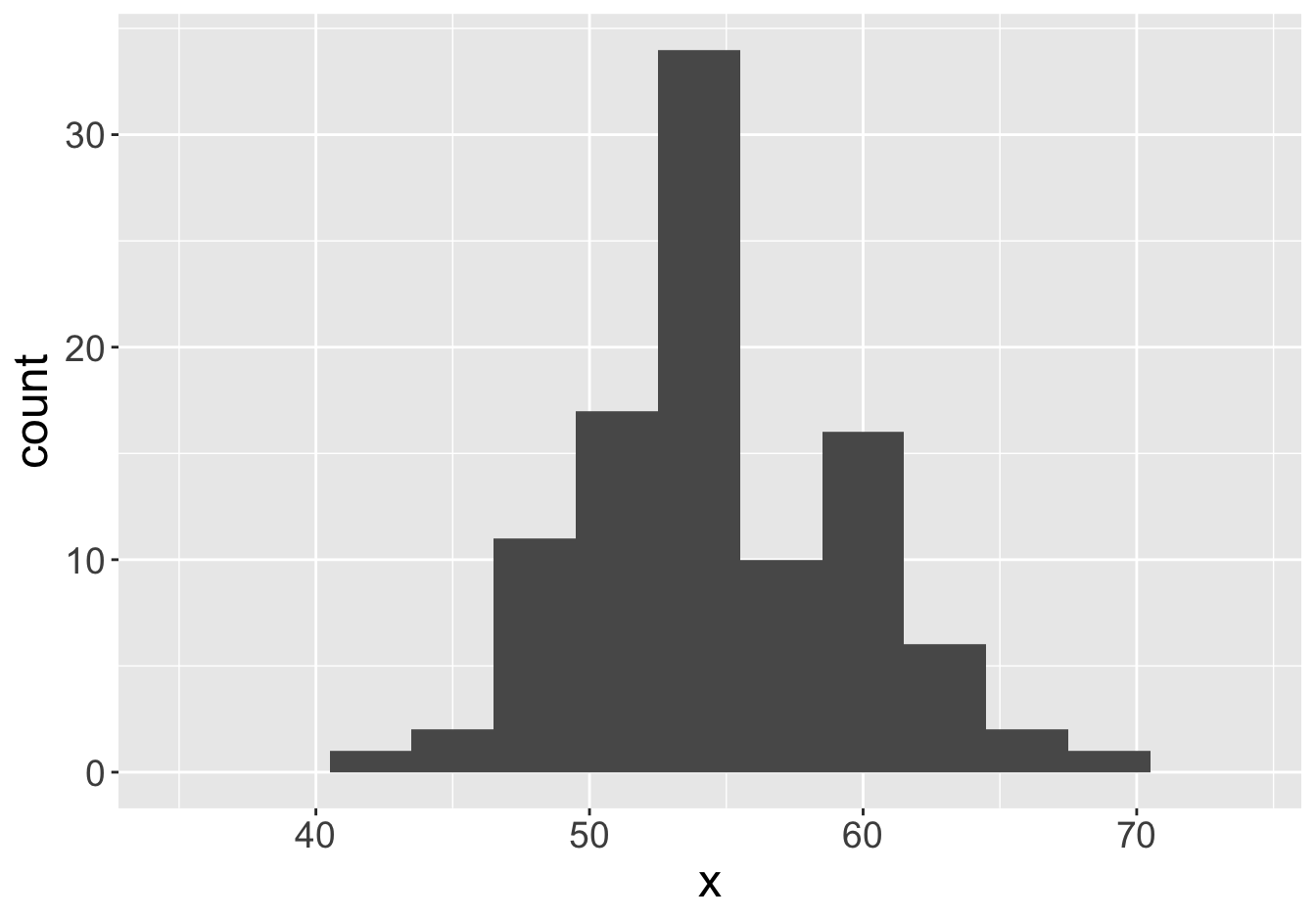
Mean: 54.84

Example - Means (Sample Size 100)

Mean: 55.06

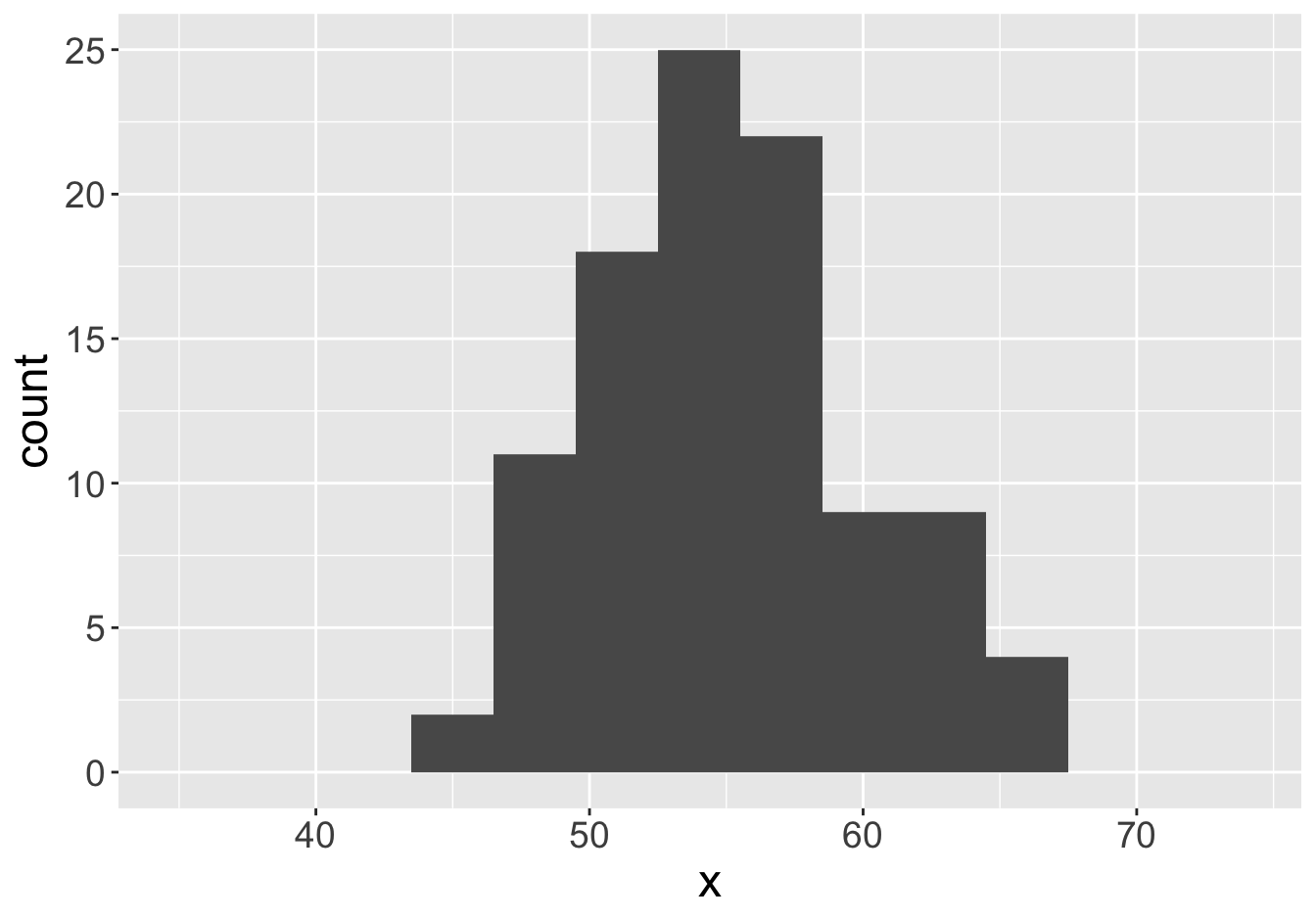
Mean: 54.98

Example - Means (Sample Size 100)

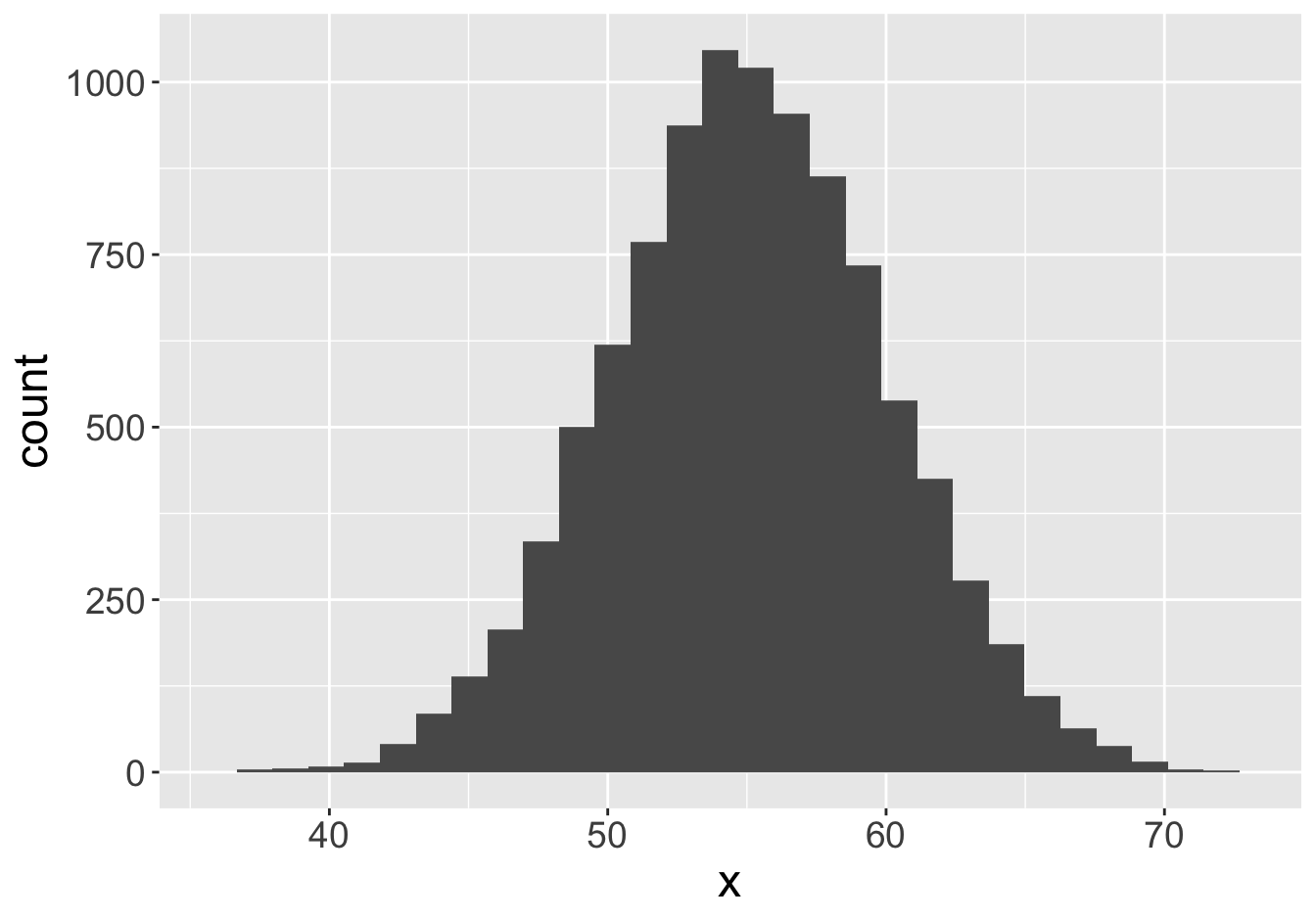
Mean: 55.06

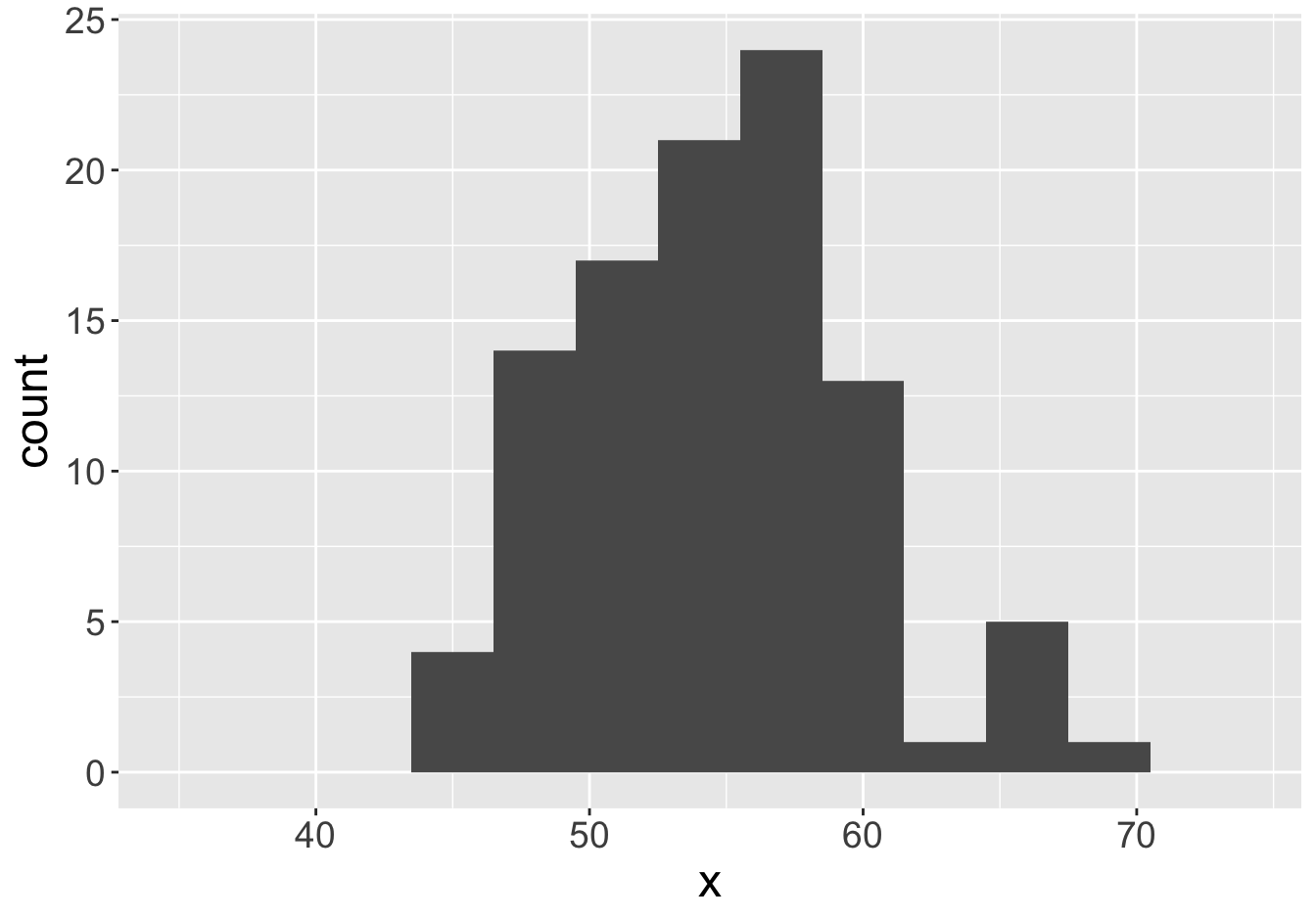
Mean: 54.58

Example - Means (Sample Size 100)

Mean: 55.06

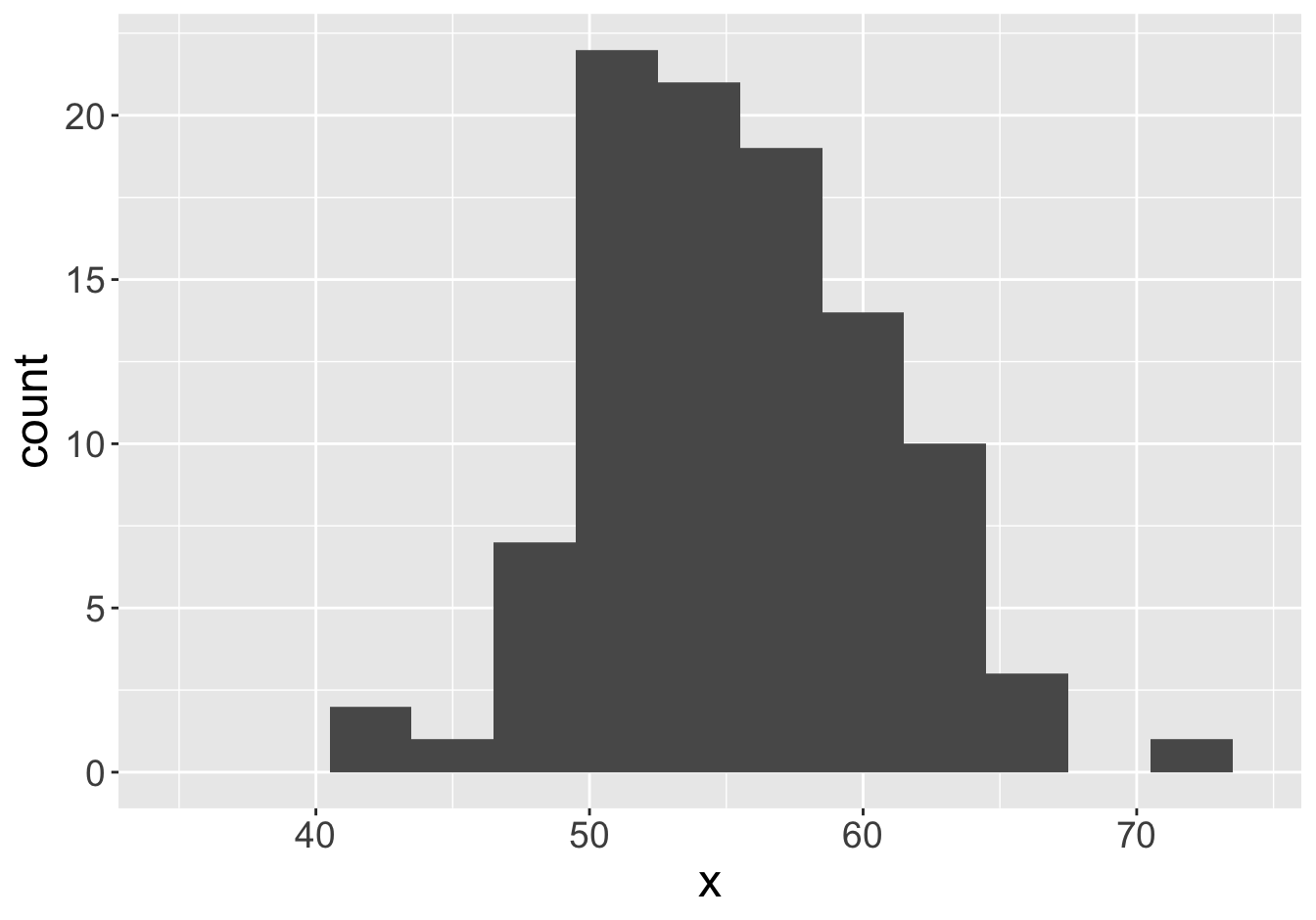
Mean: 55.57

Example - Means (Sample Size 100)

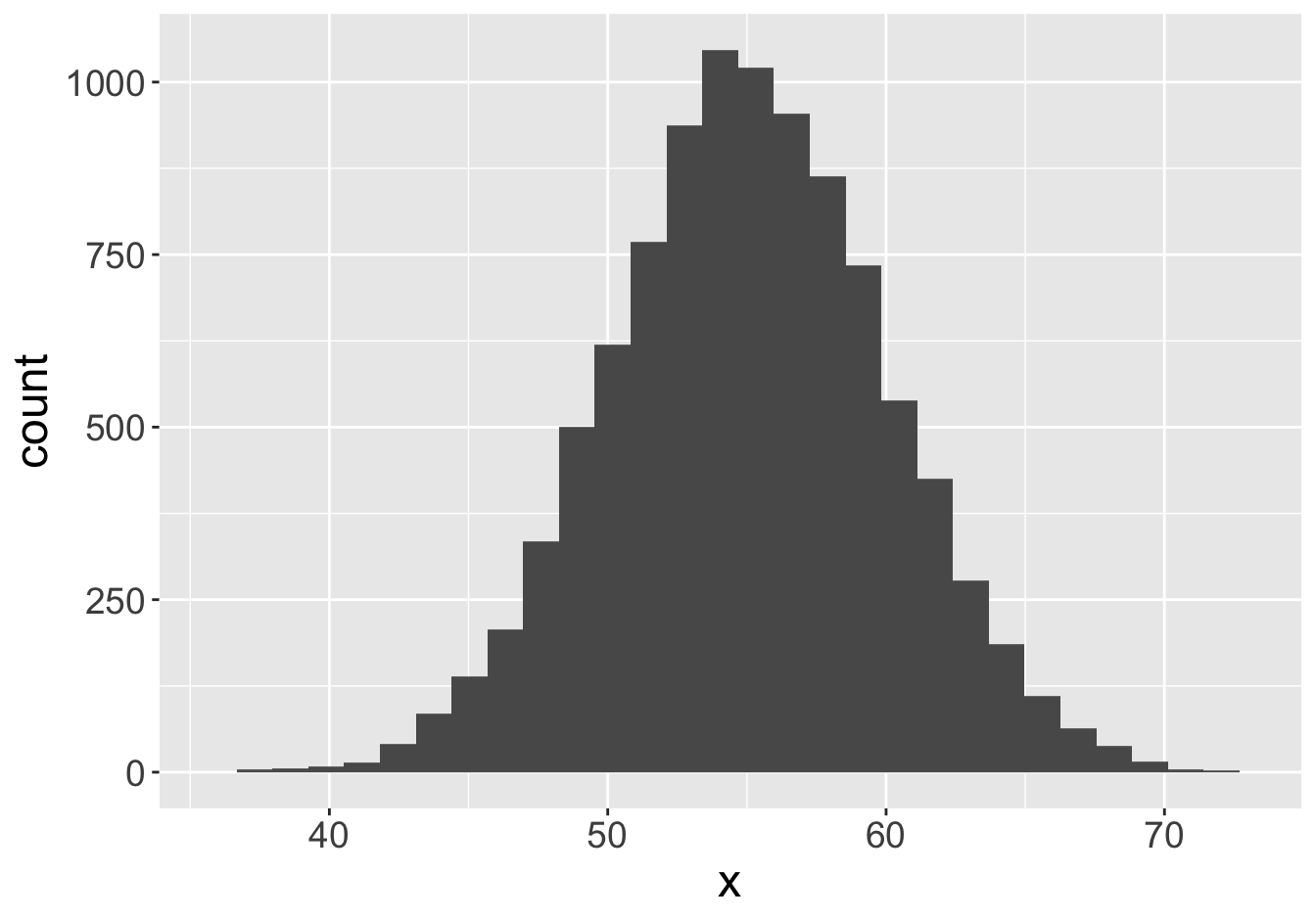
Mean: 55.06

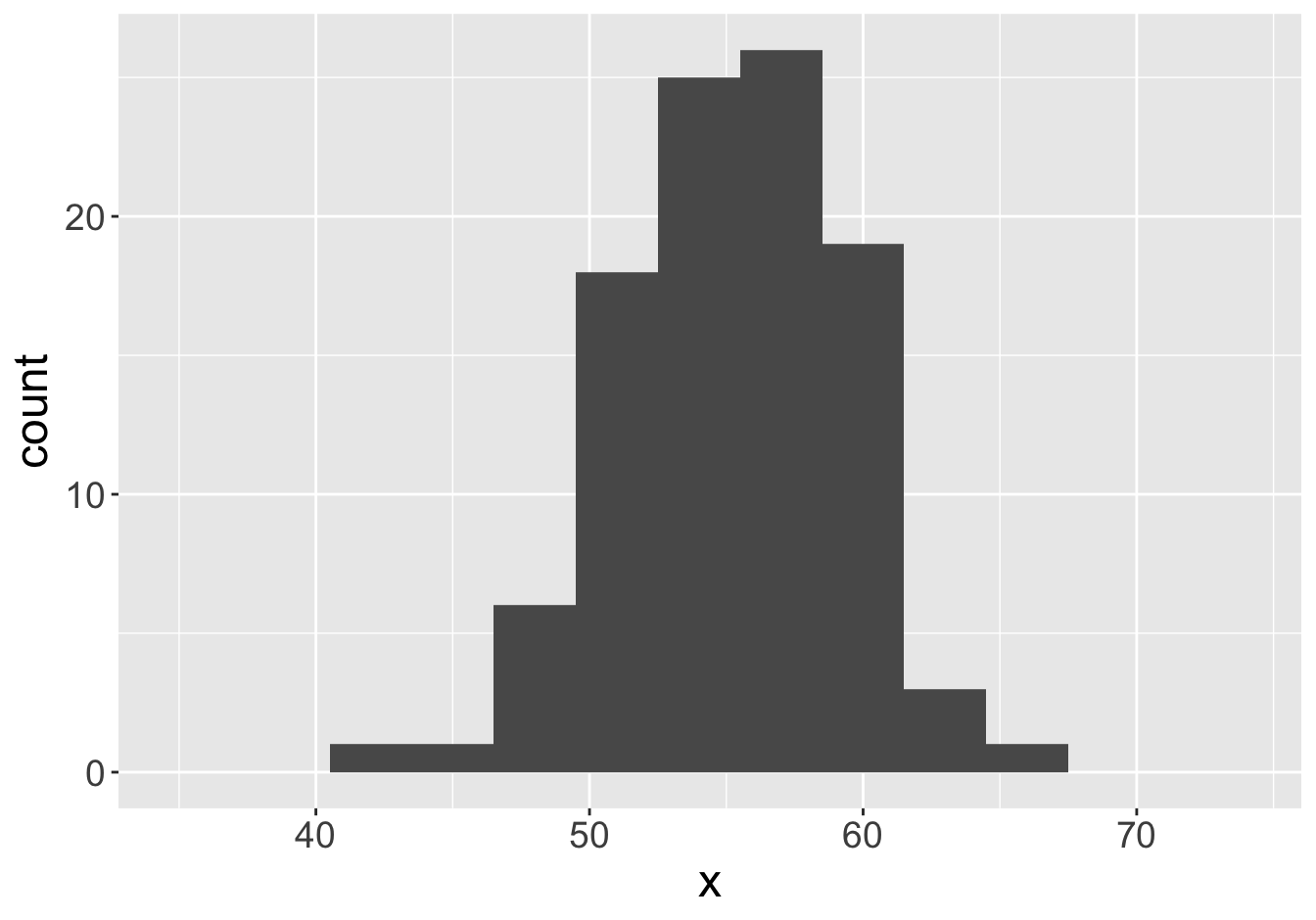
Mean: 55.12

Example - Means (Sample Size 100)

Mean: 55.06

Mean: 55.29

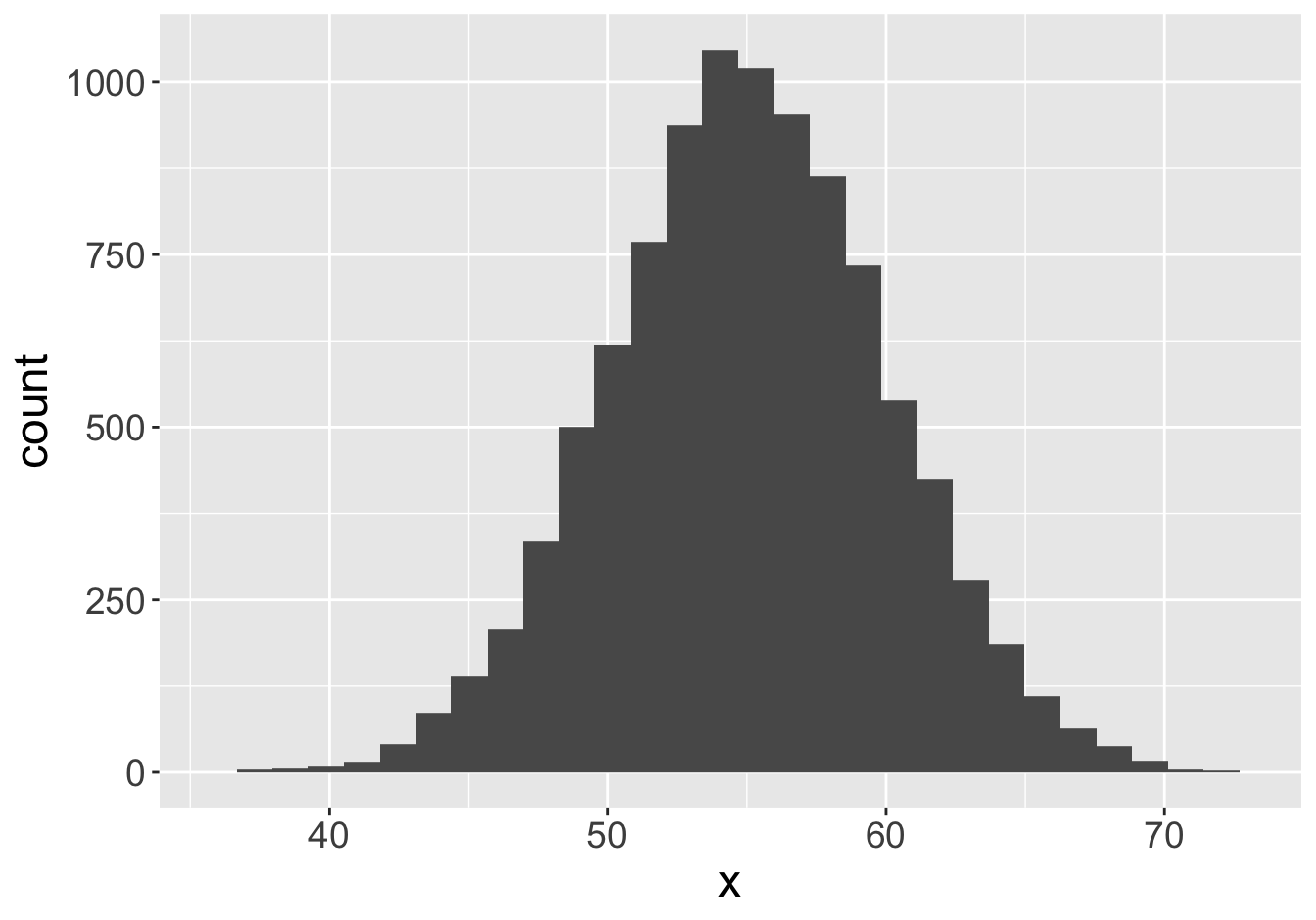
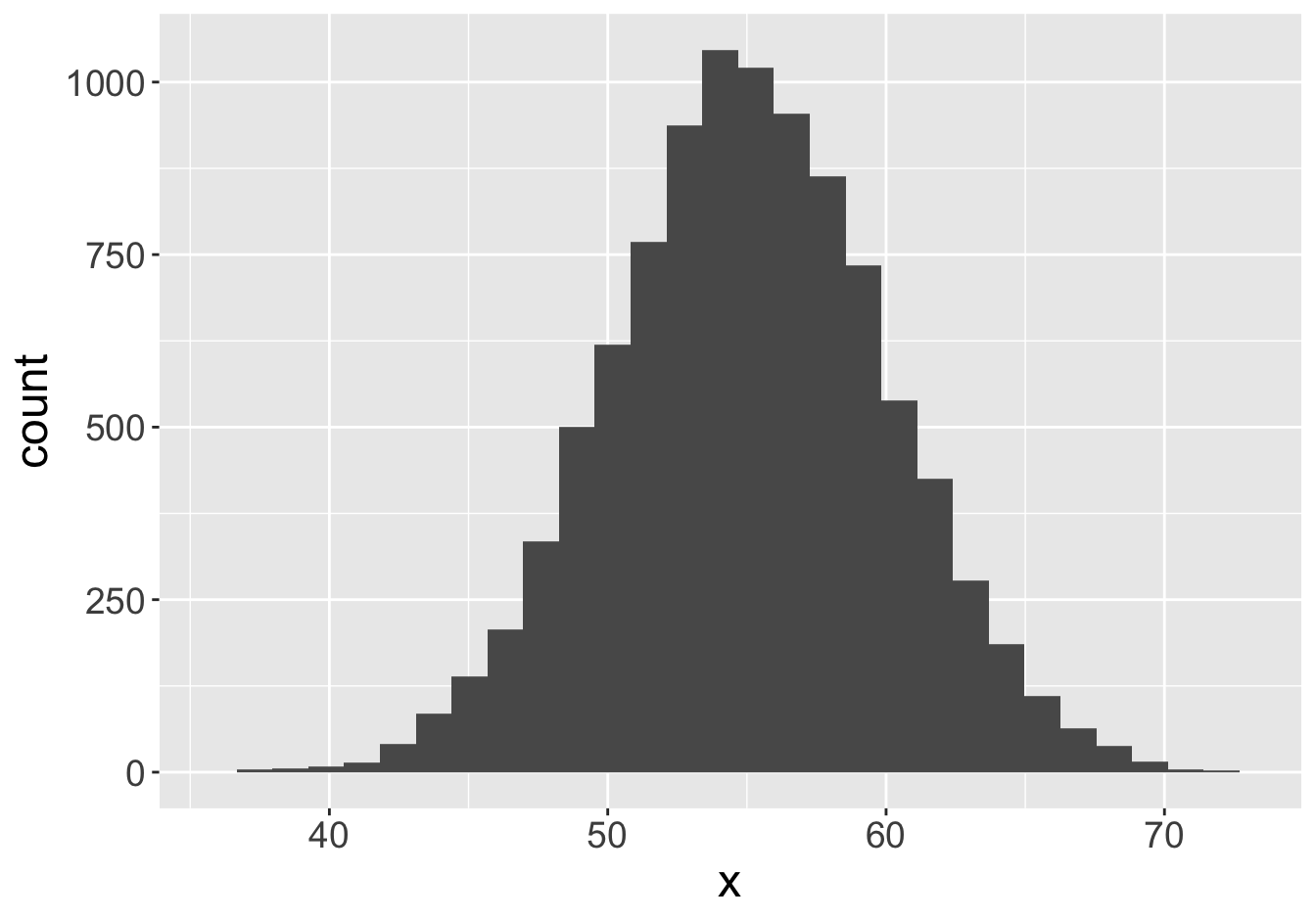
Example - Means (Sample Size 1000)

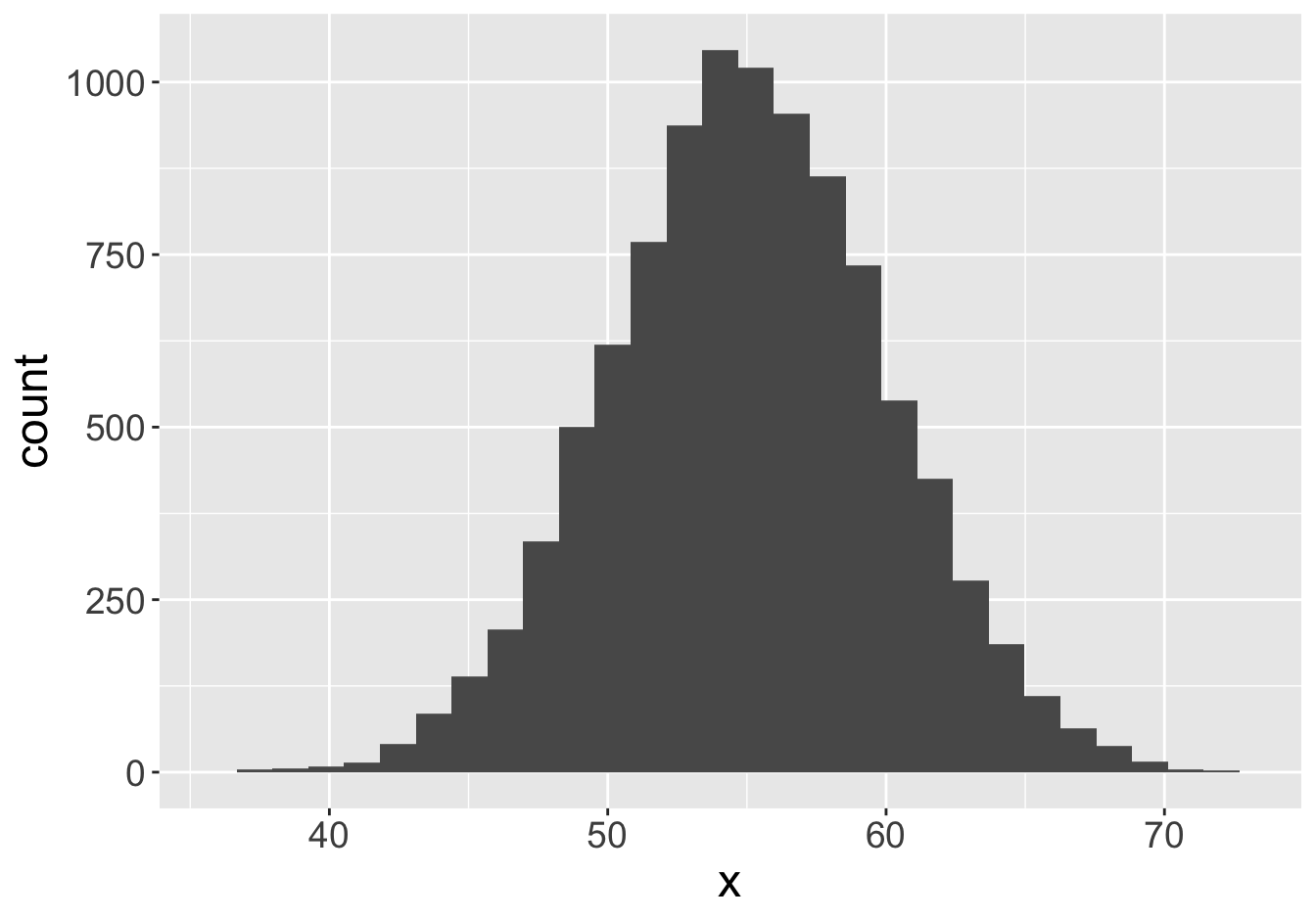
Mean: 55.06

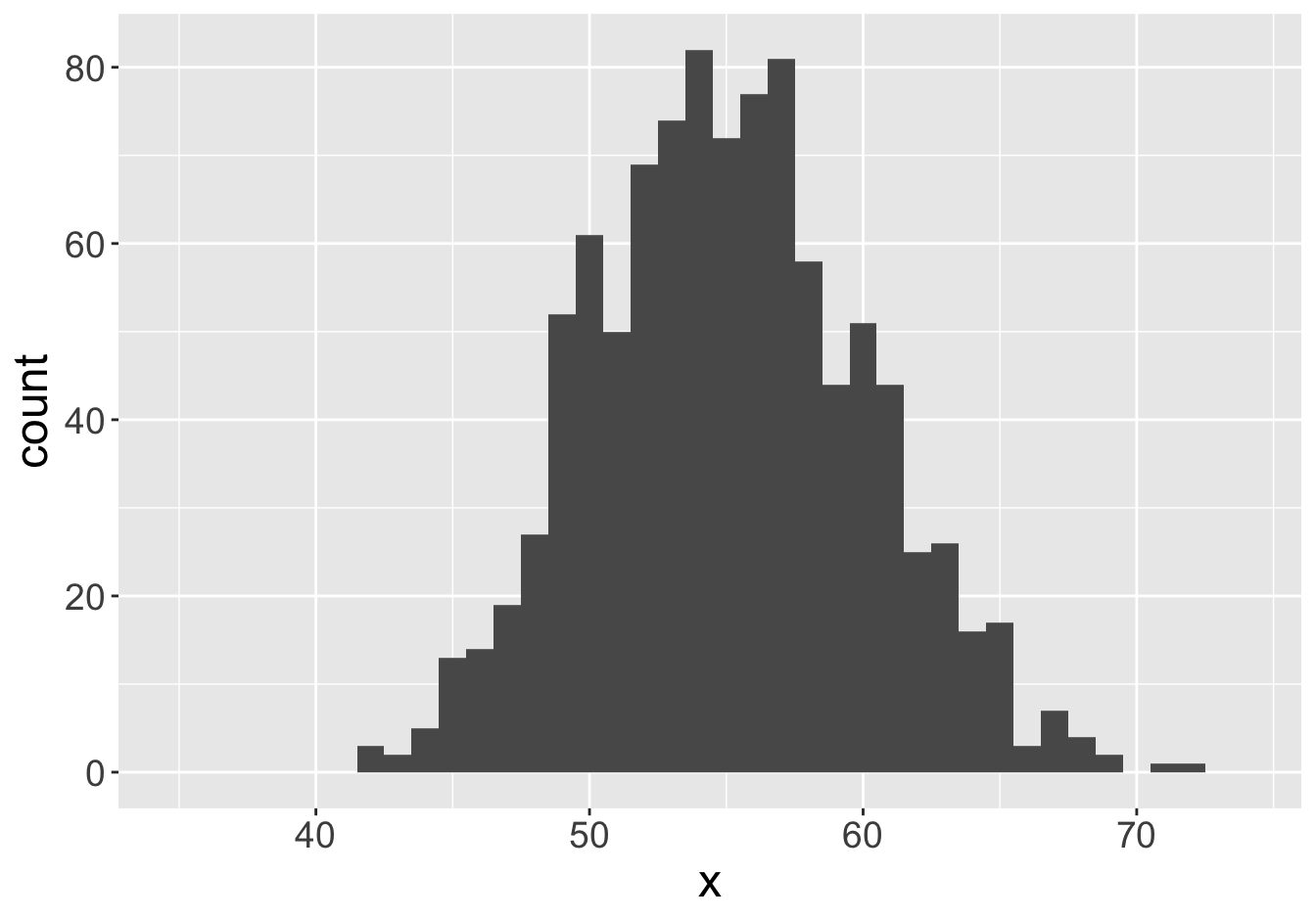
Mean: 55.07

Example - Means (Sample Size 1000)

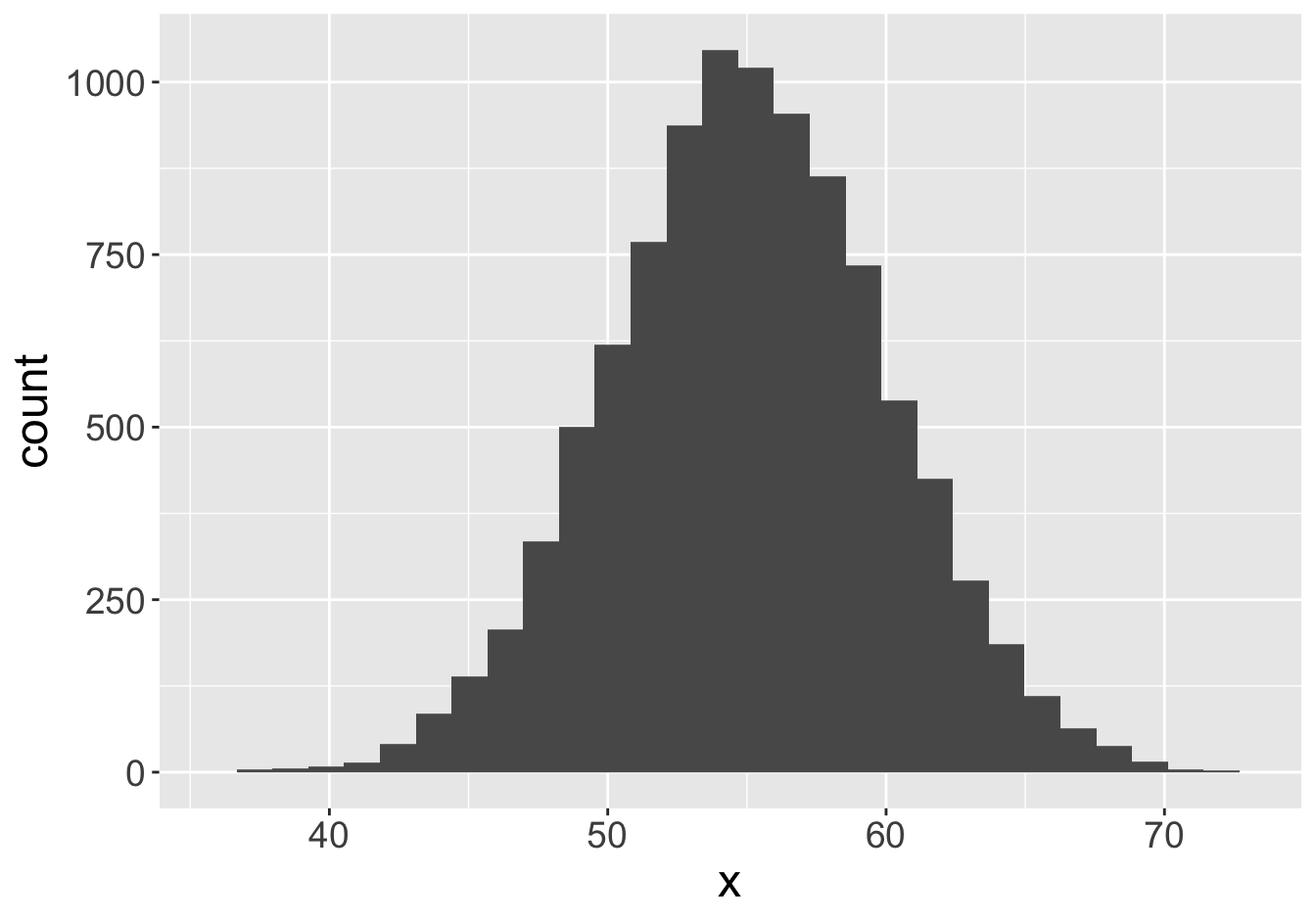
Mean: 55.06

Mean: 55.06

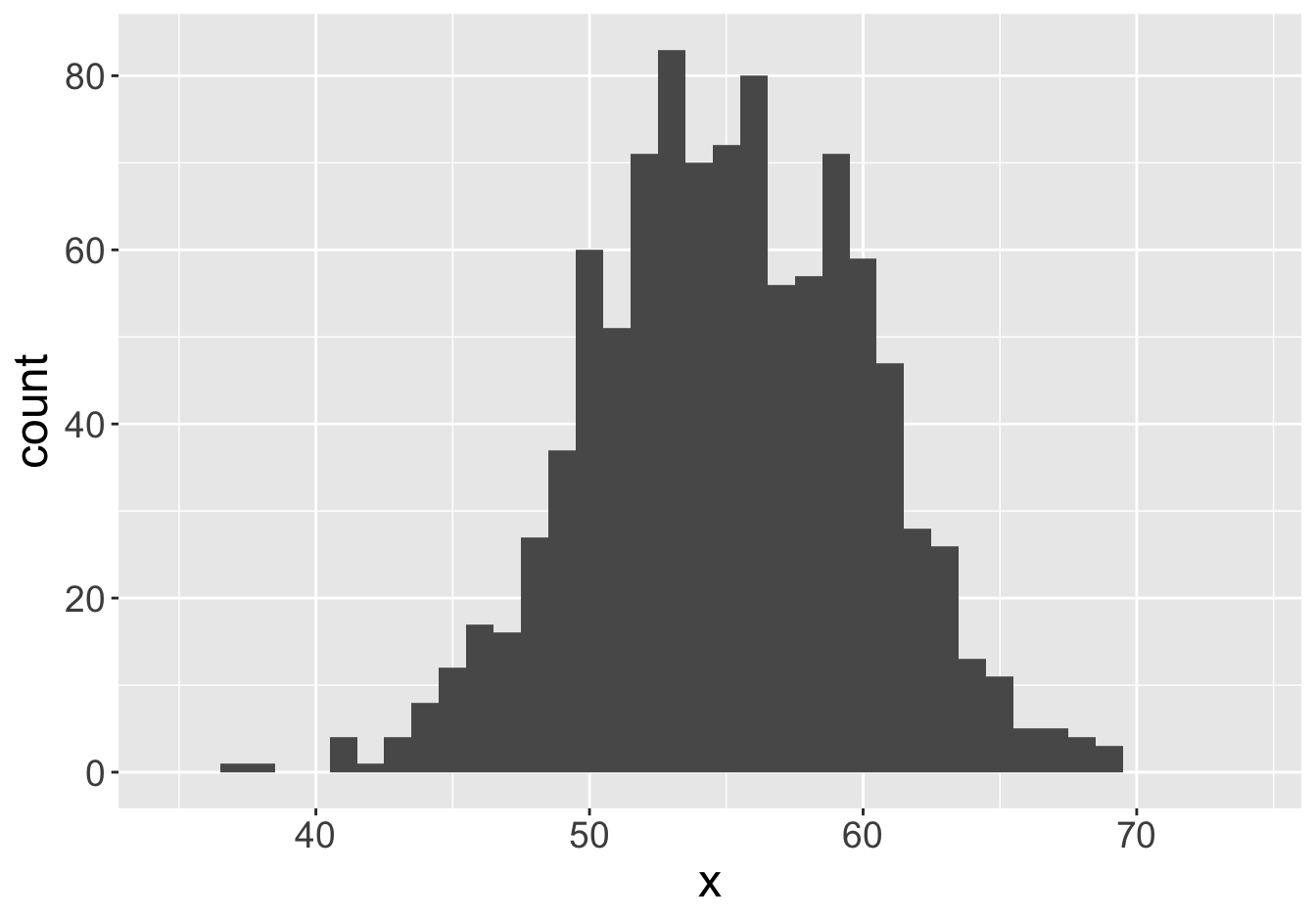
Example - Means (Sample Size 1000)

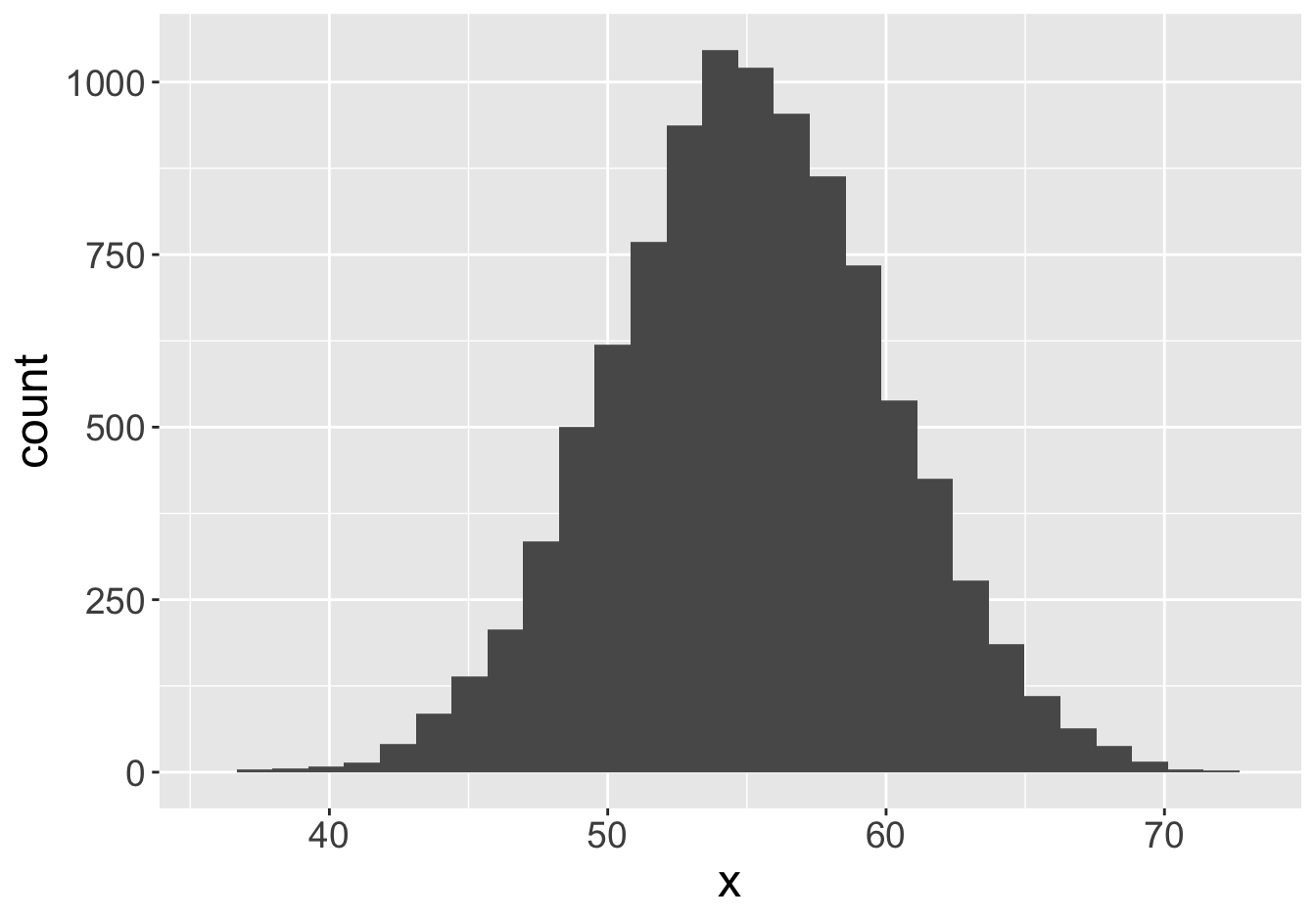
Mean: 55.06

Mean: 55.05

Example - Means

How confident would you feel stating that the population mean is equal to any of these values?

Example - Slopes

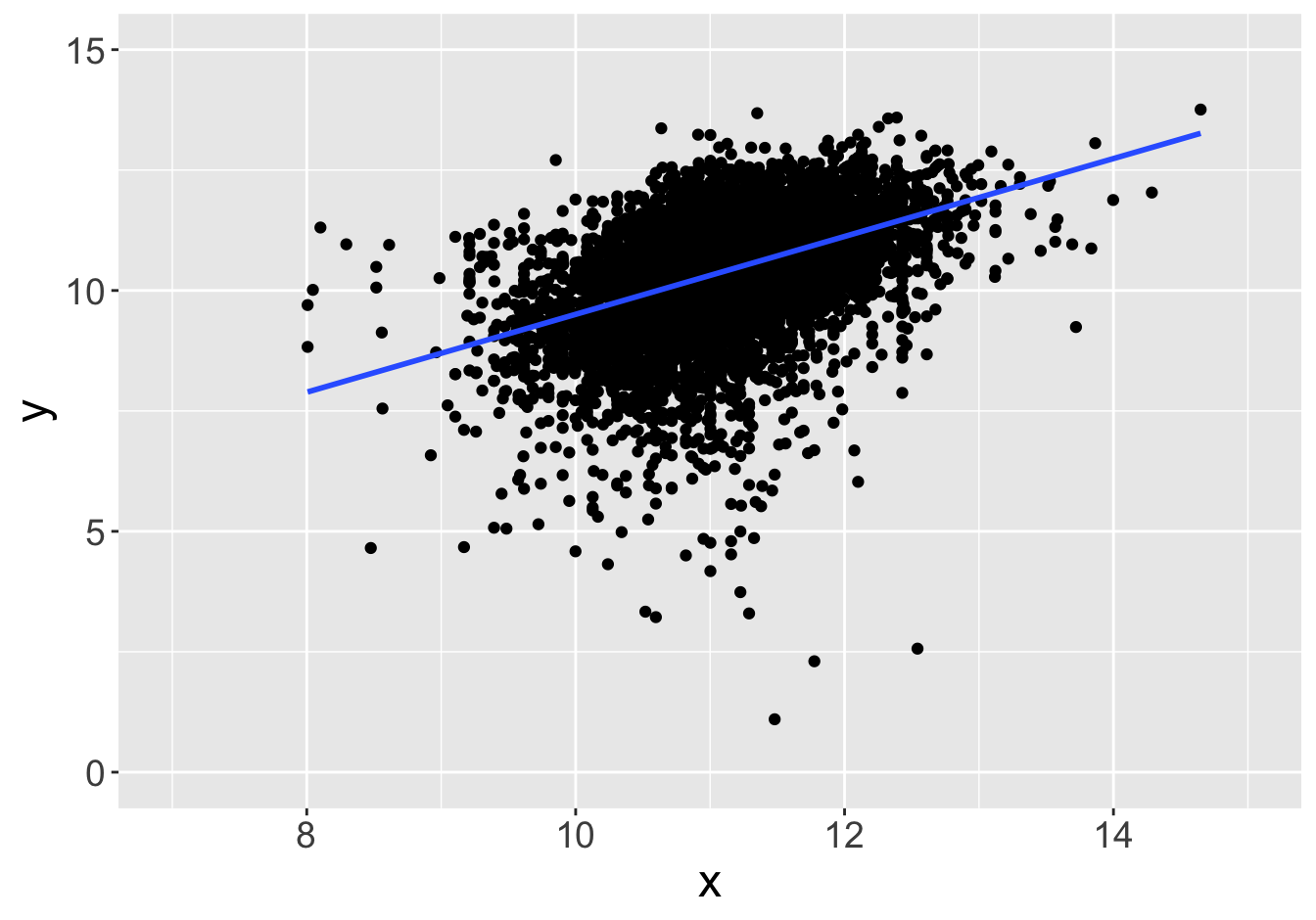
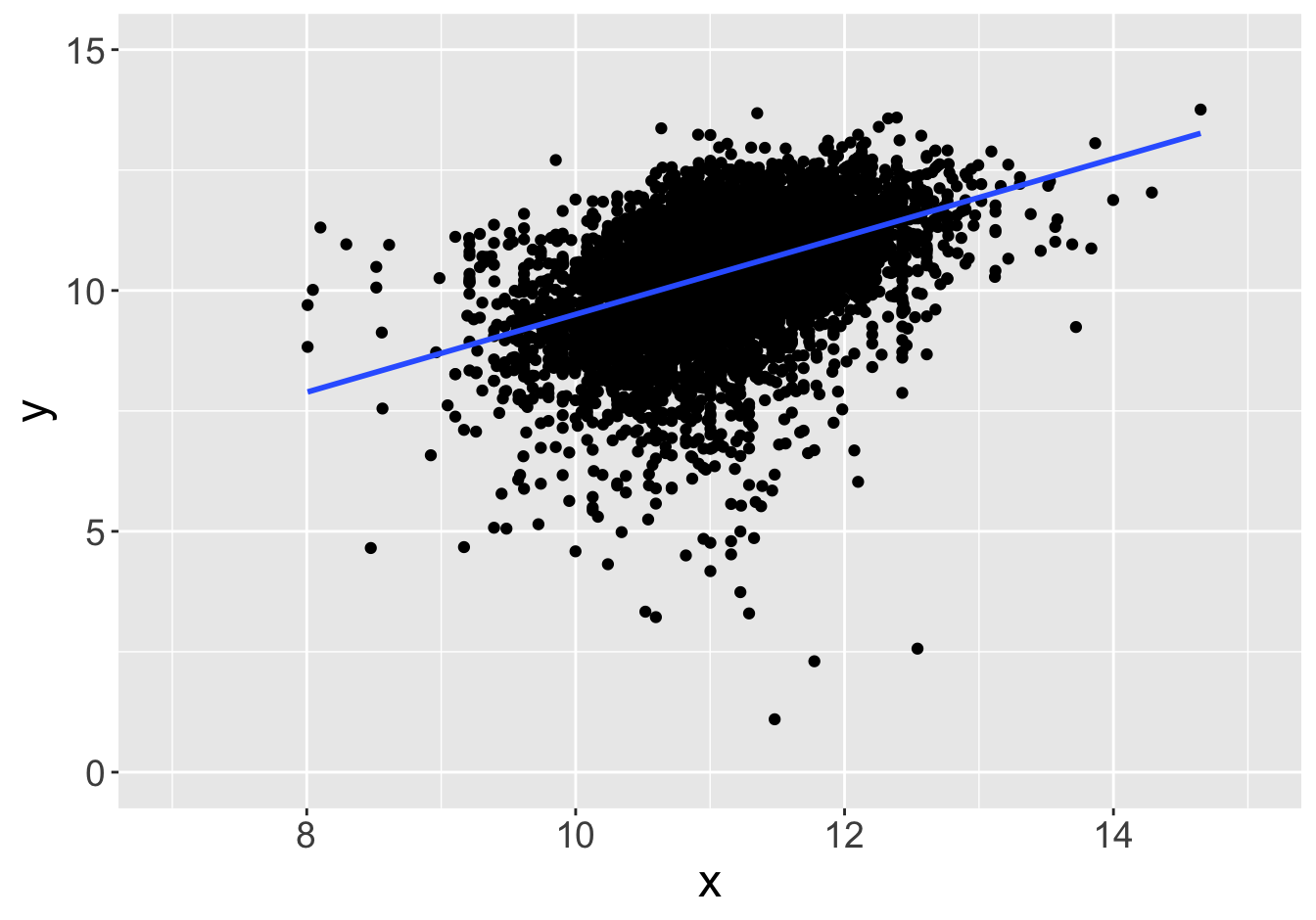
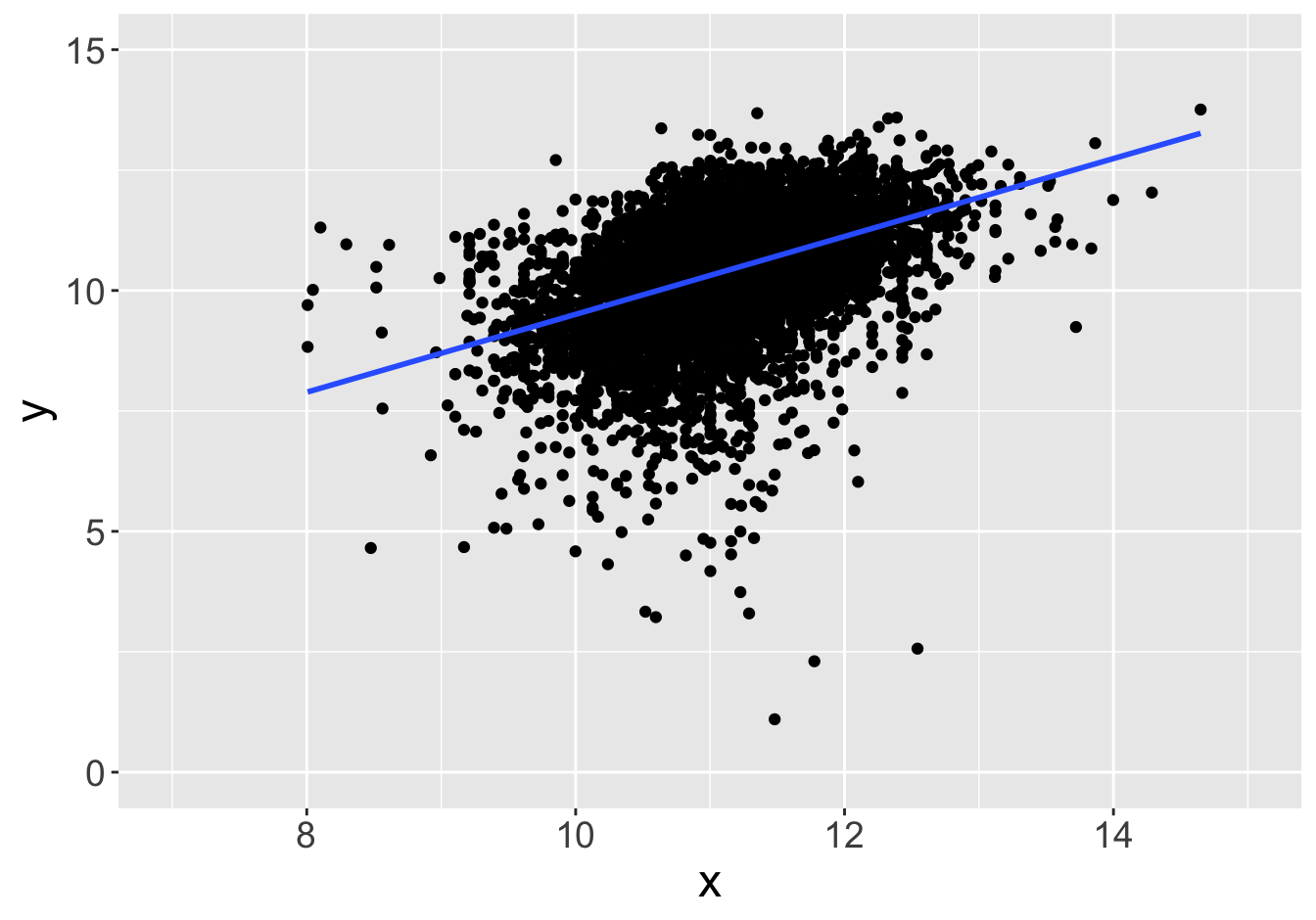
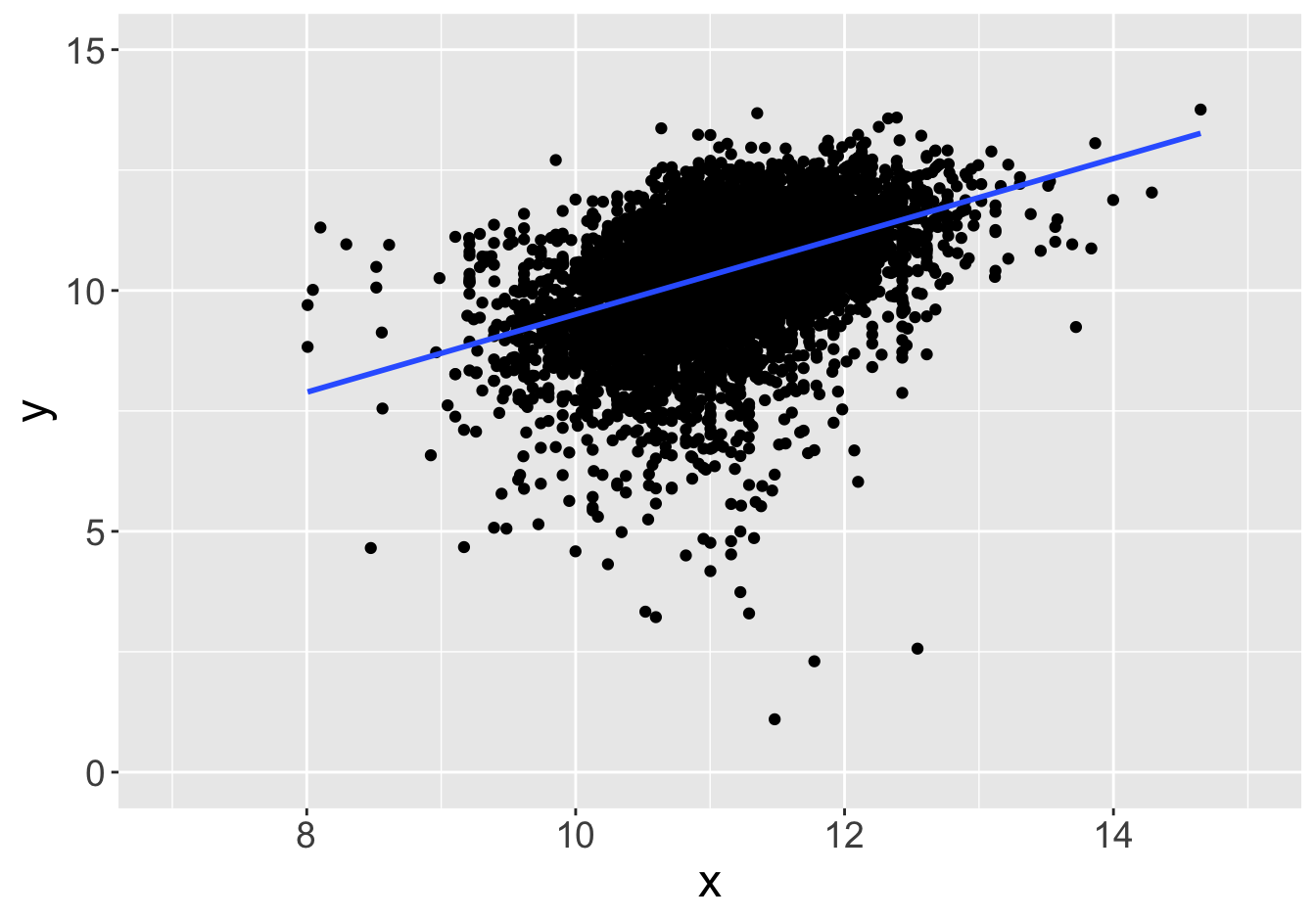
Suppose this scatter plot represents some values \(x, y\) in a population of 10,000:

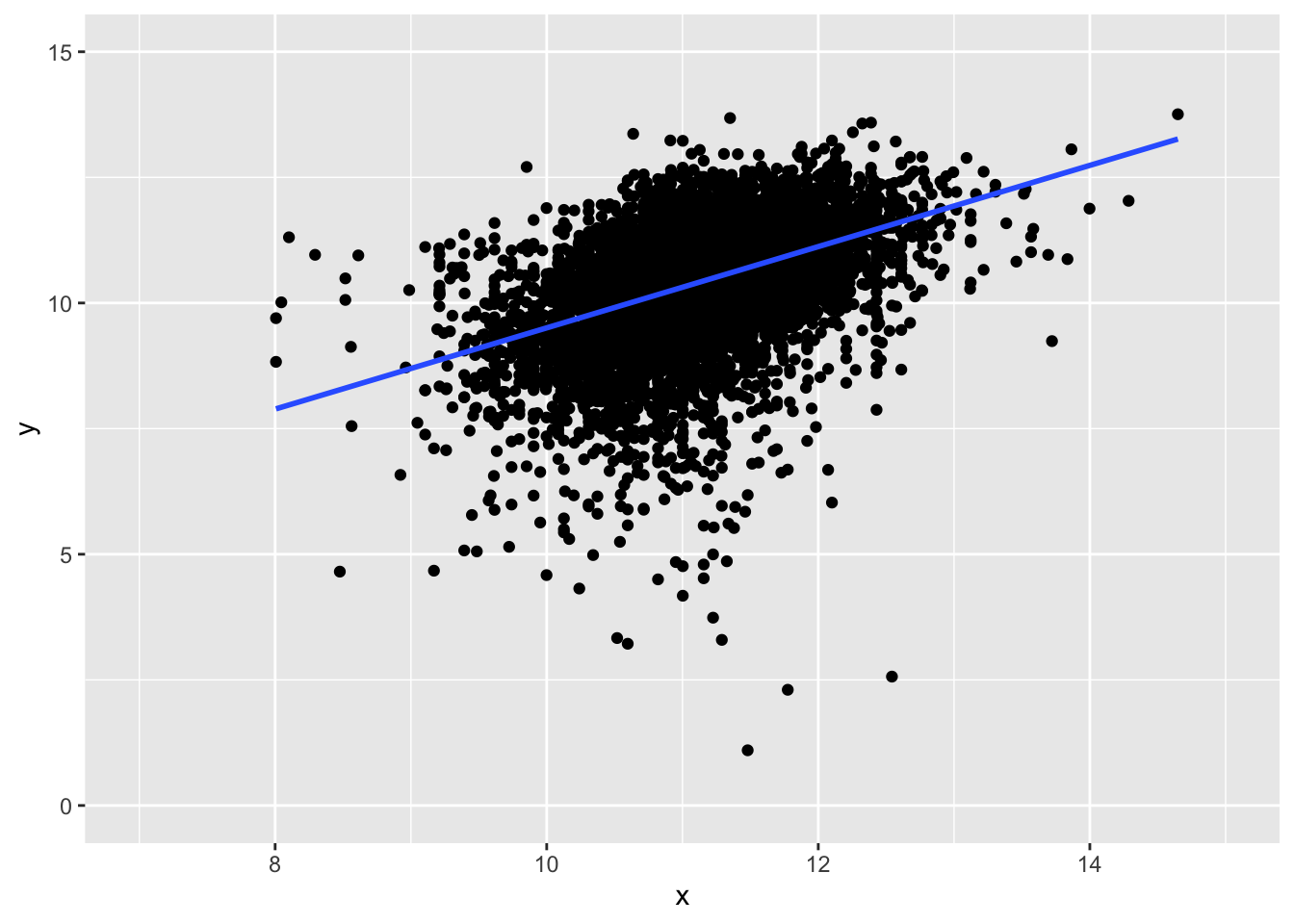
Slope: 0.81

Example - Slopes (Sample Size 2)

Slope: 0.81

Slope: 5.97

Example - Slopes (Sample Size 2)

Slope: 0.81

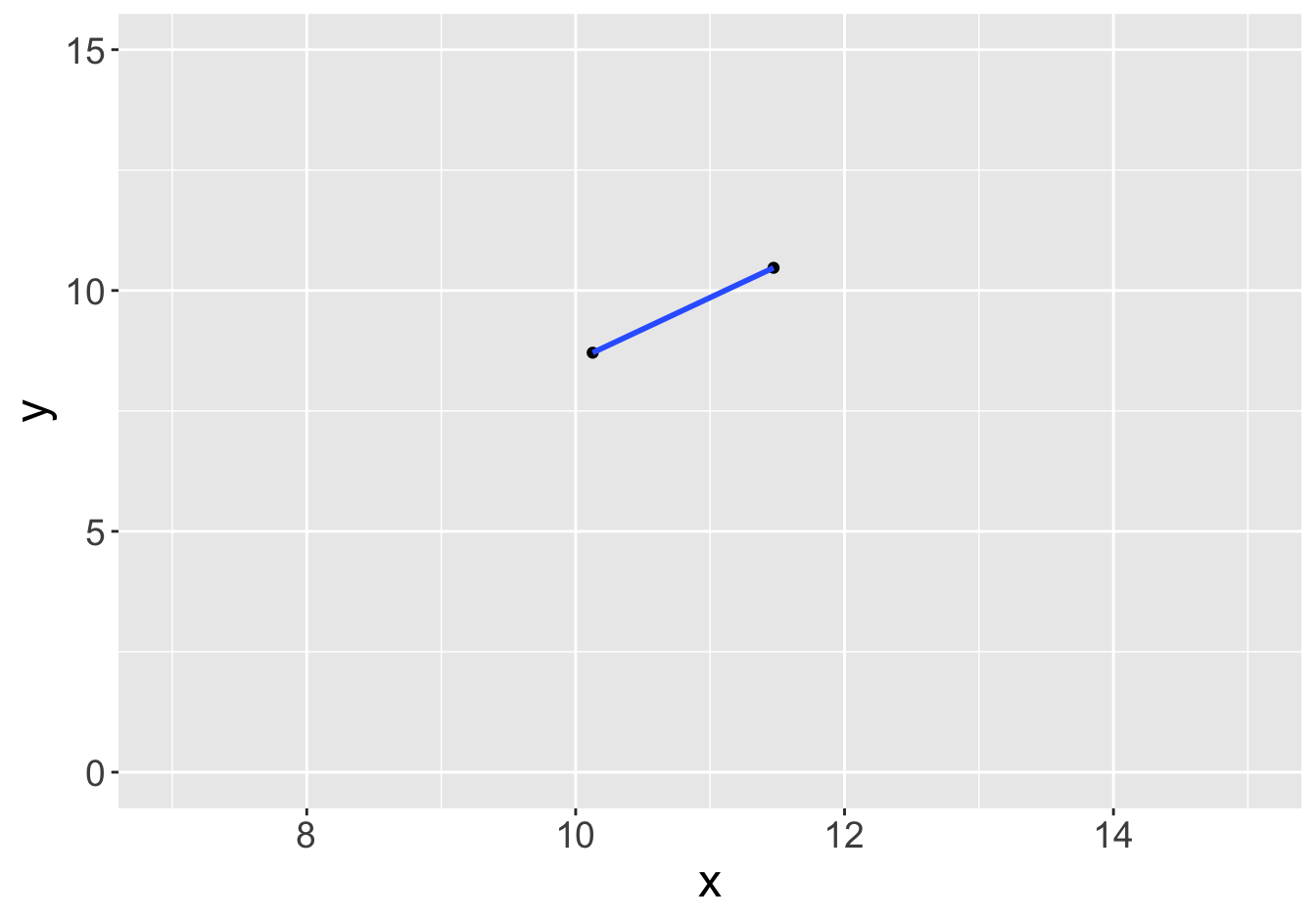
Slope: 1.31

Example - Slopes (Sample Size 2)

Slope: 0.81

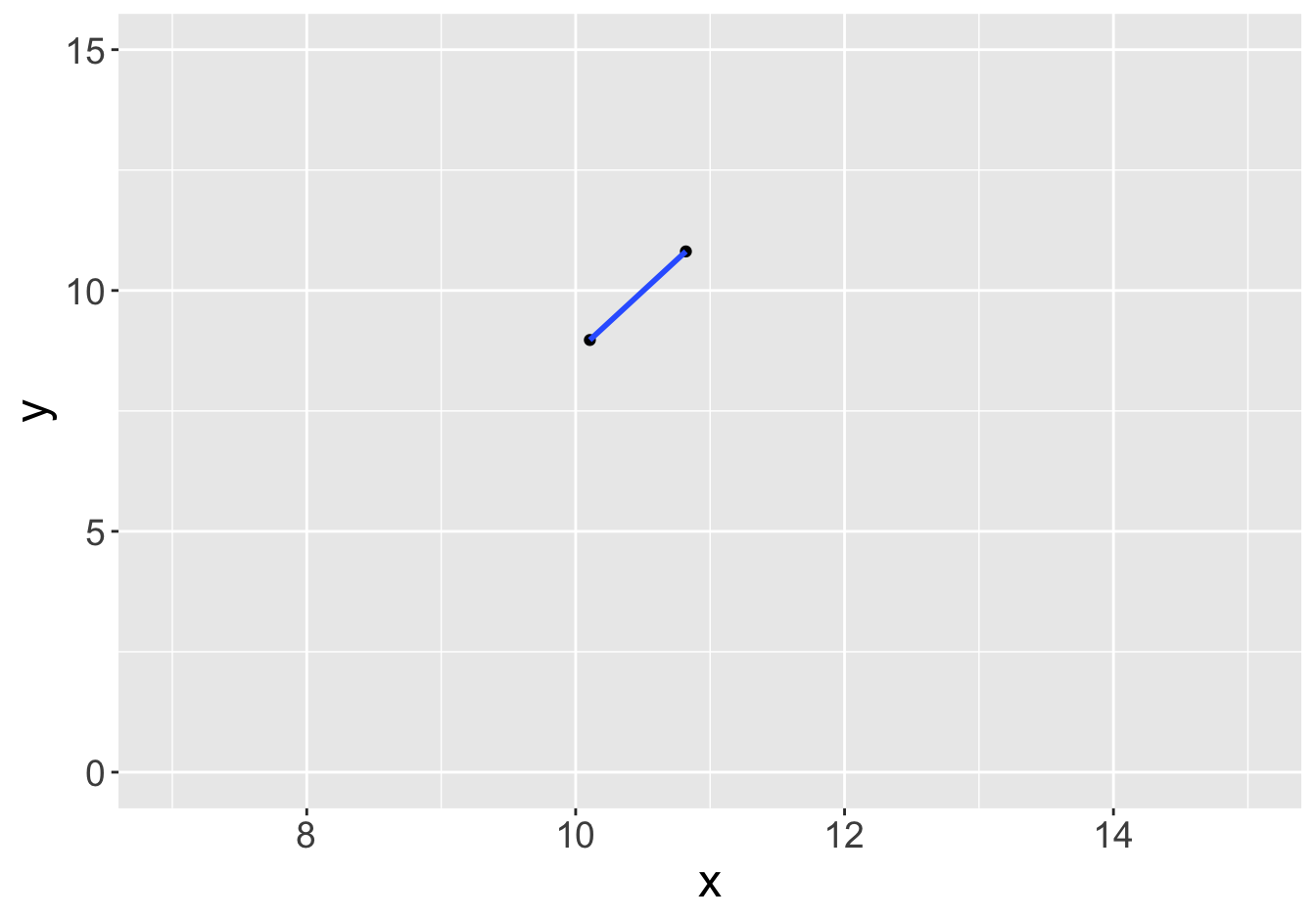
Slope: 2.57

Example - Slopes (Sample Size 2)

Slope: 0.81

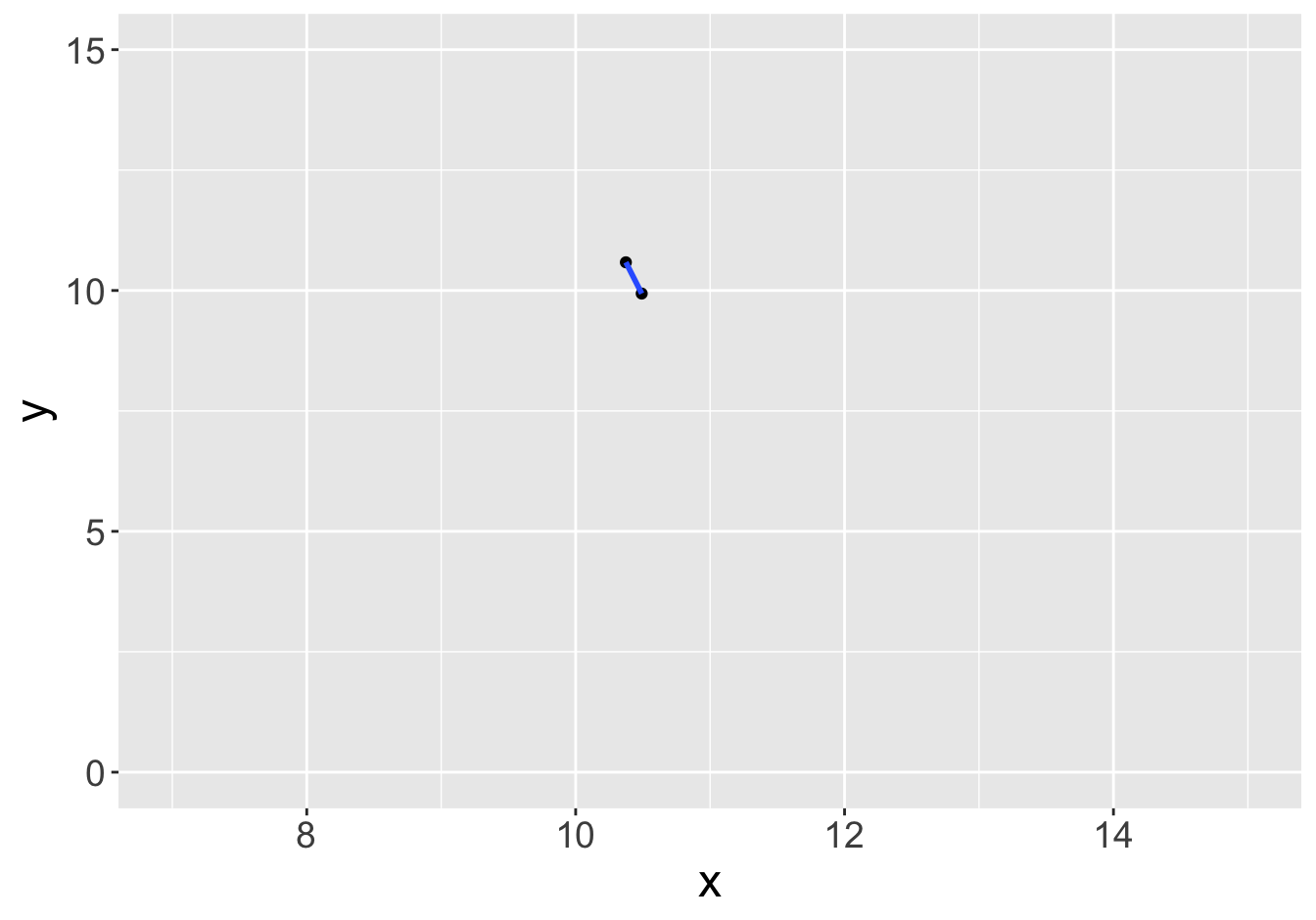
Slope: -5.51

Example - Slopes (Sample Size 10)

Slope: 0.81

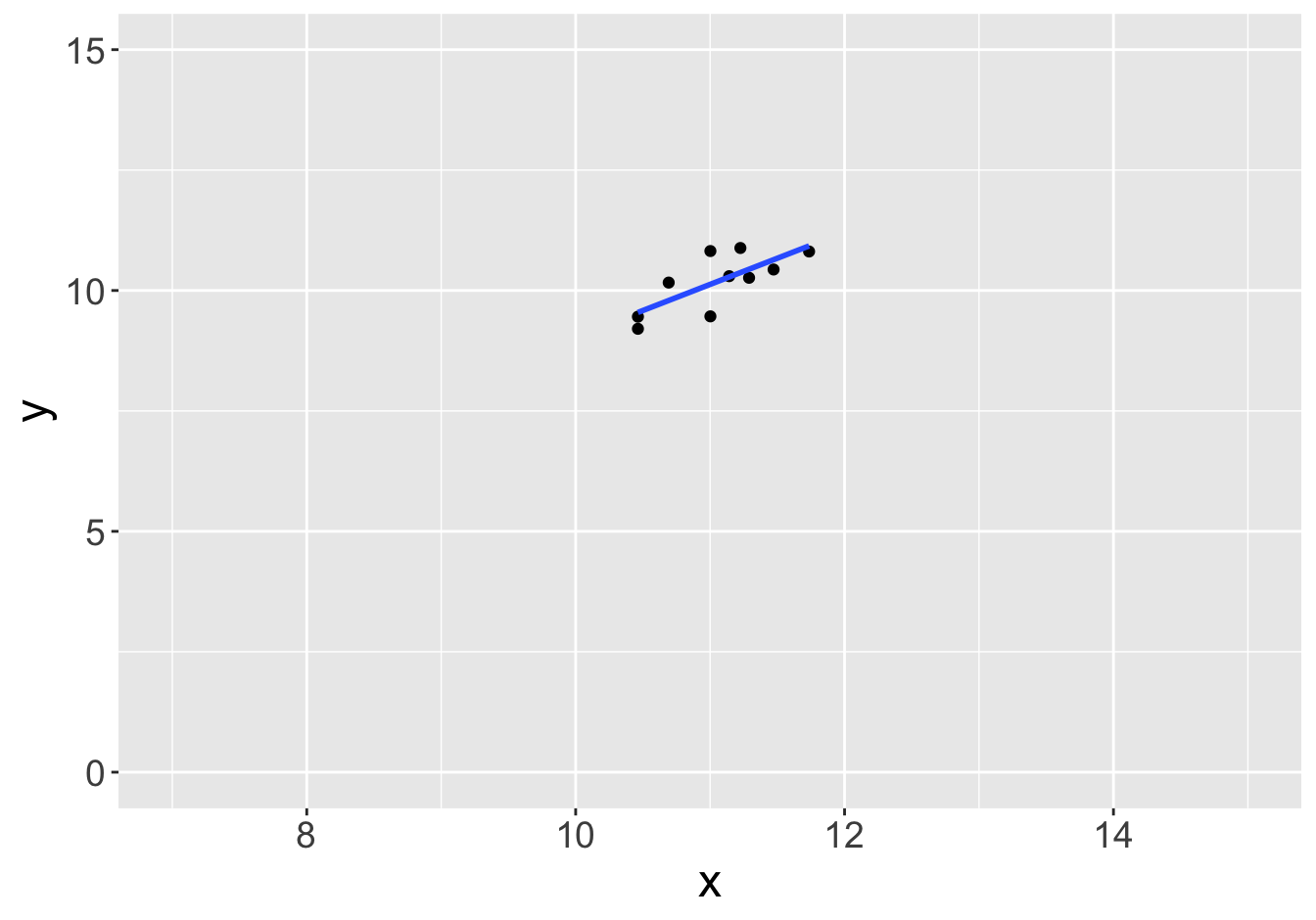
Slope: 1.08

Example - Slopes (Sample Size 10)

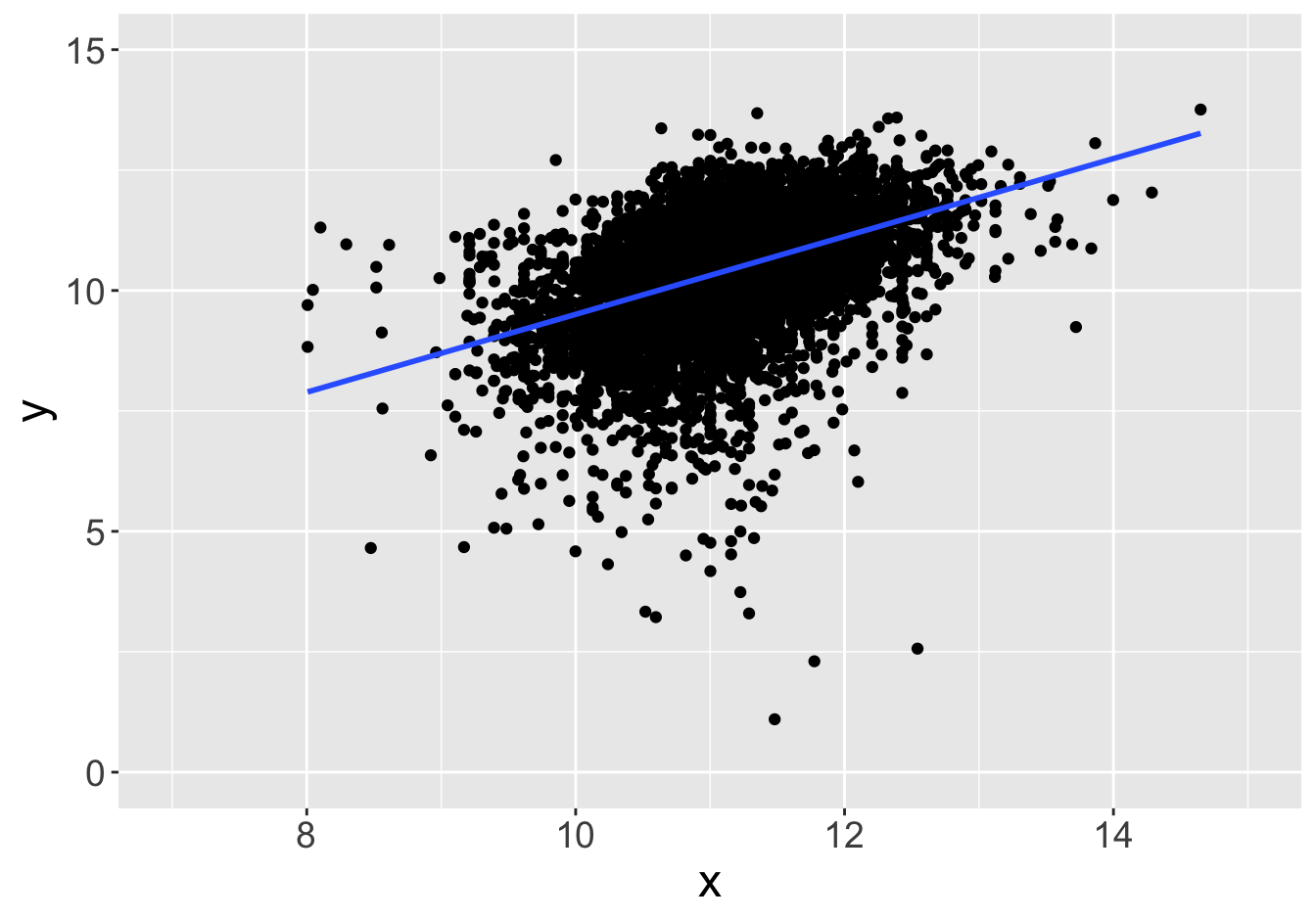
Slope: 0.81

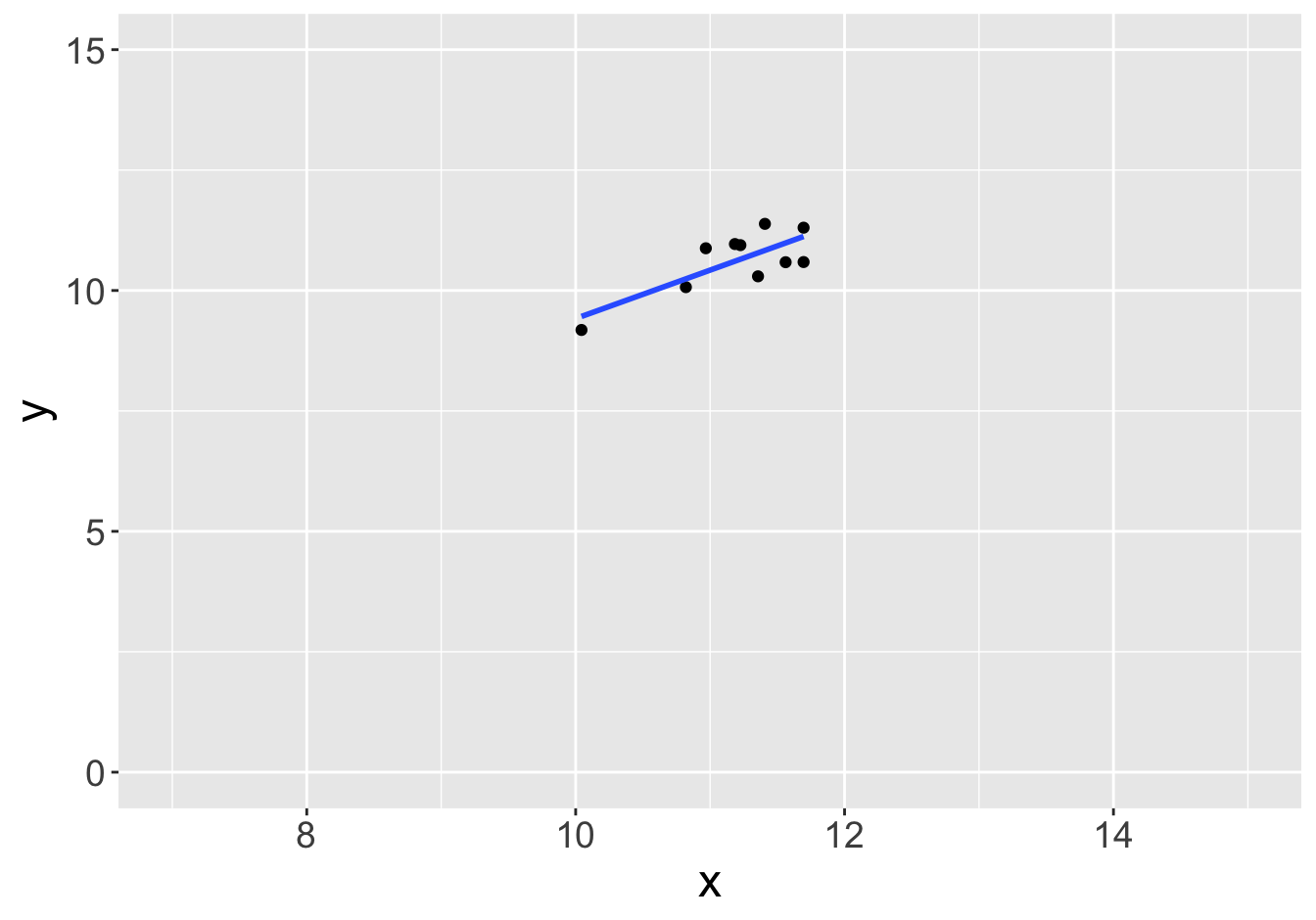
Slope: 1.01

Example - Slopes (Sample Size 10)

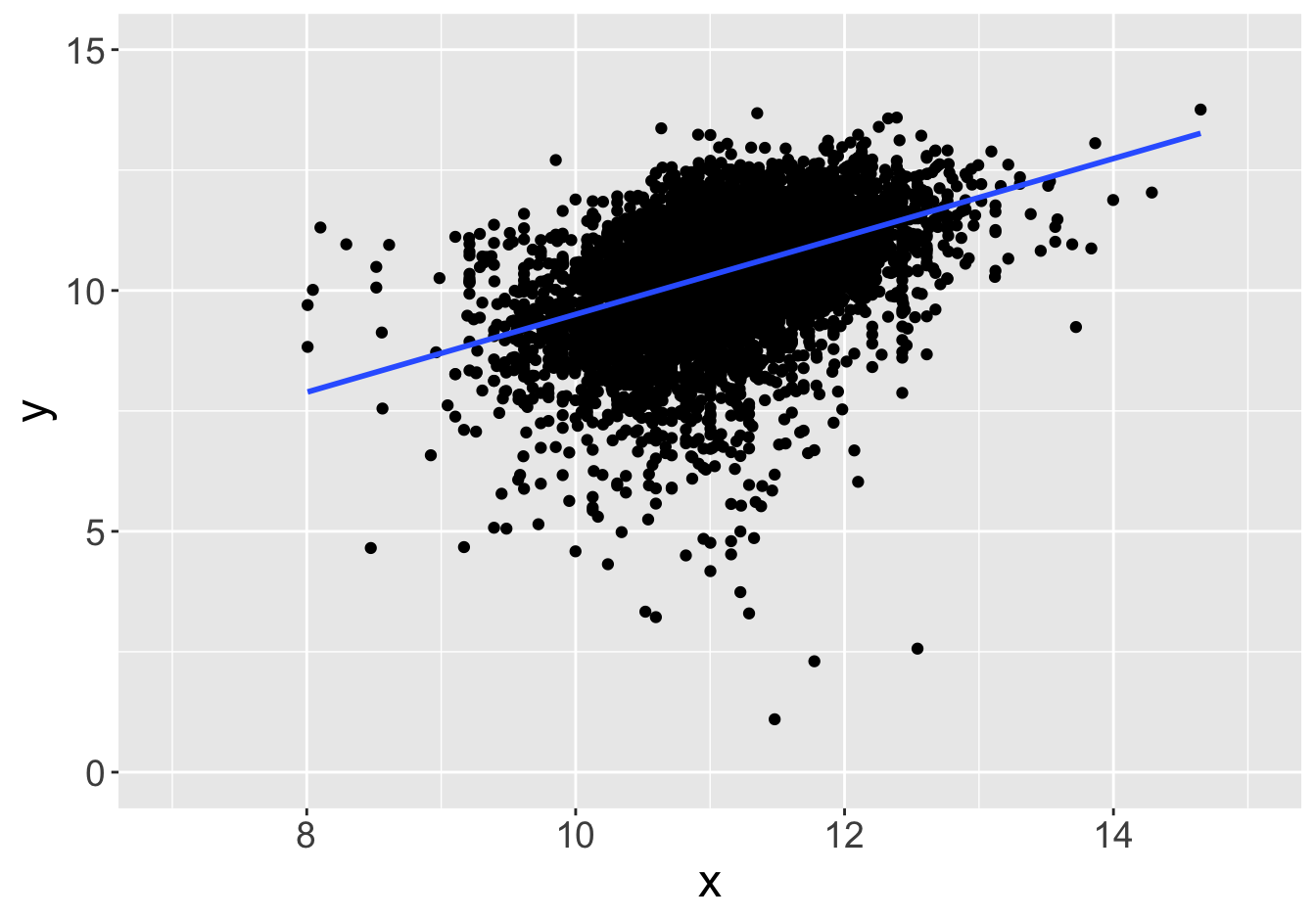
Slope: 0.81

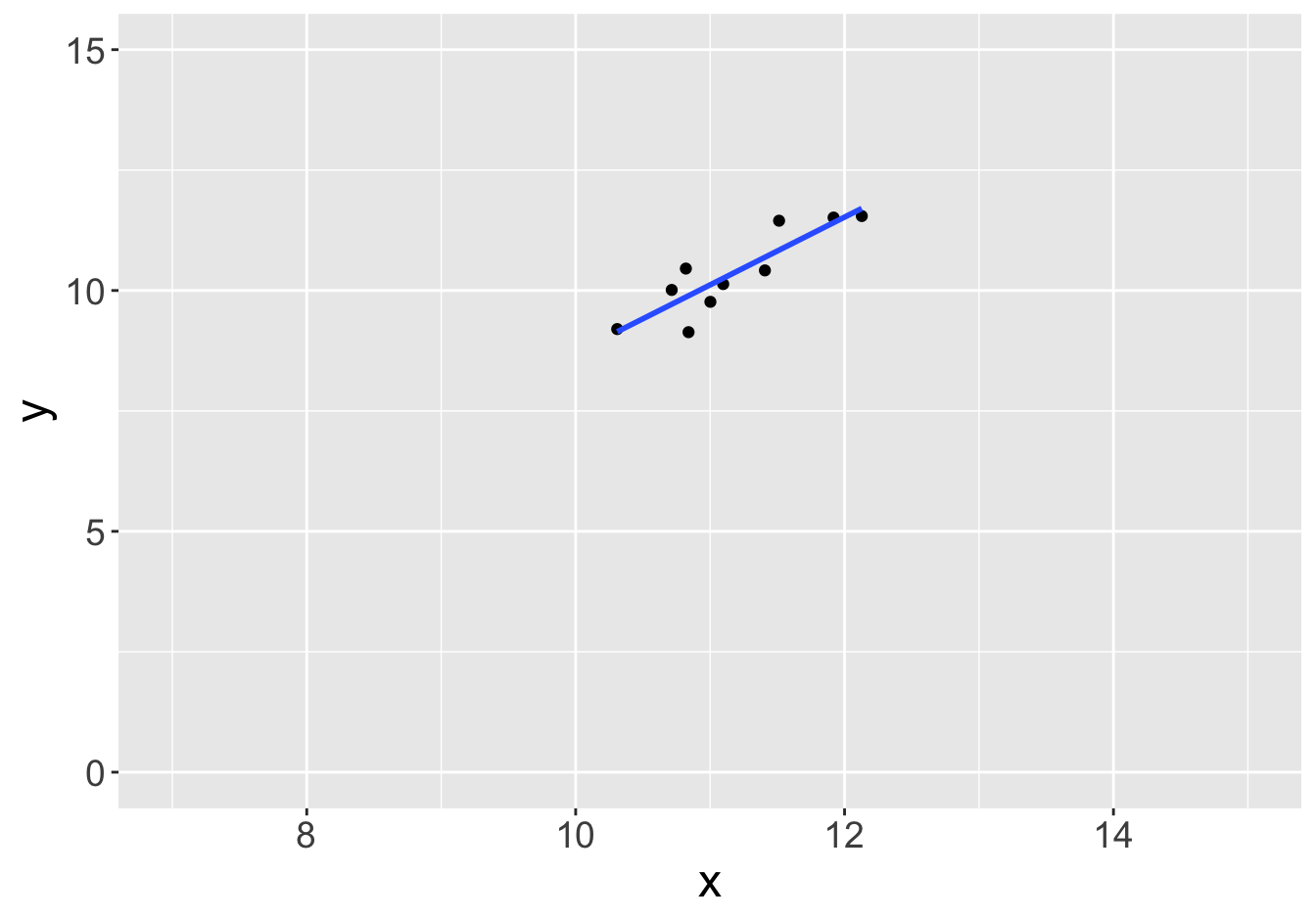
Slope: 1.41

Example - Slopes (Sample Size 10)

Slope: 0.81

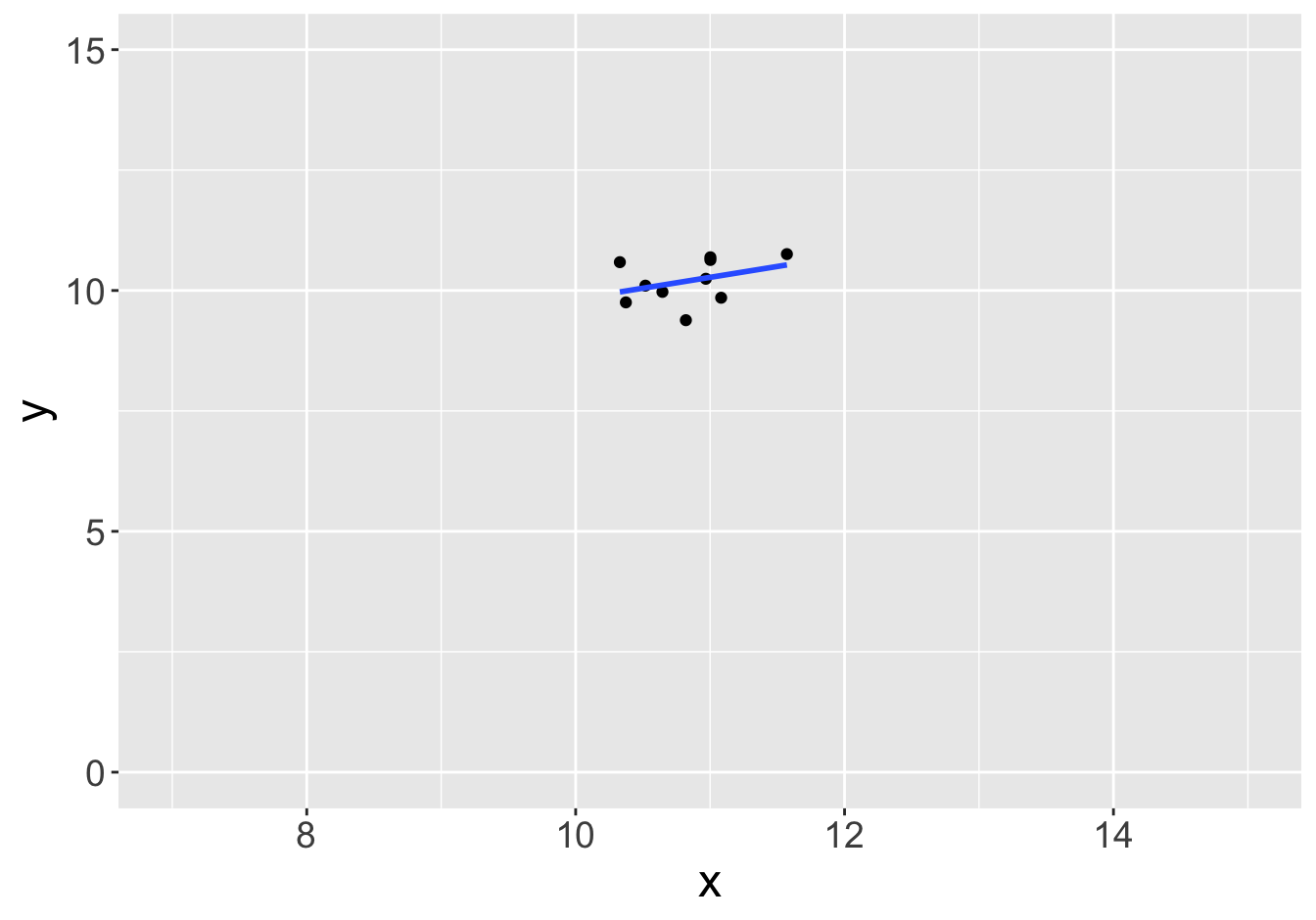
Slope: 0.45

Example - Slopes (Sample Size 100)

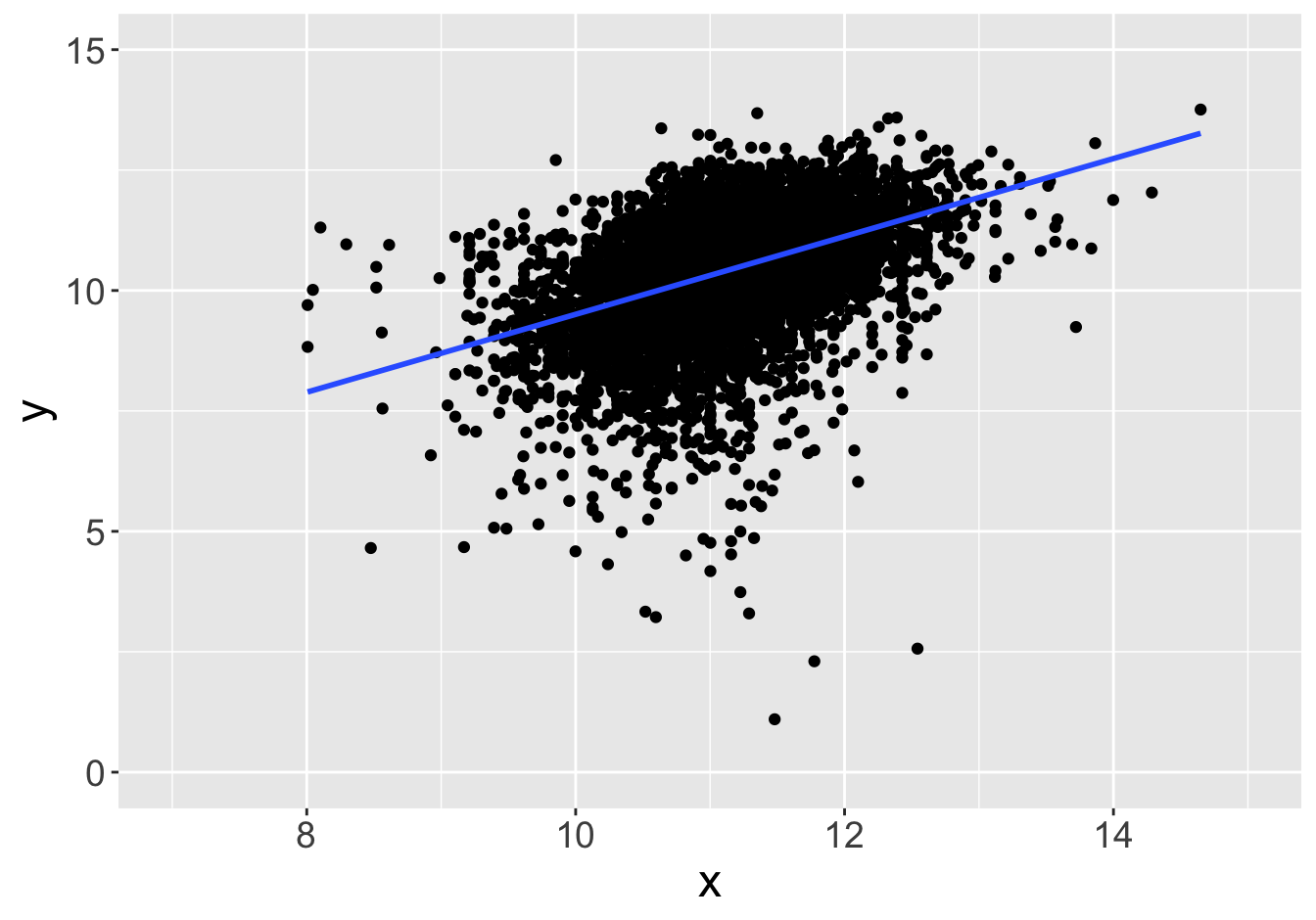
Slope: 0.81

Slope: 1.06

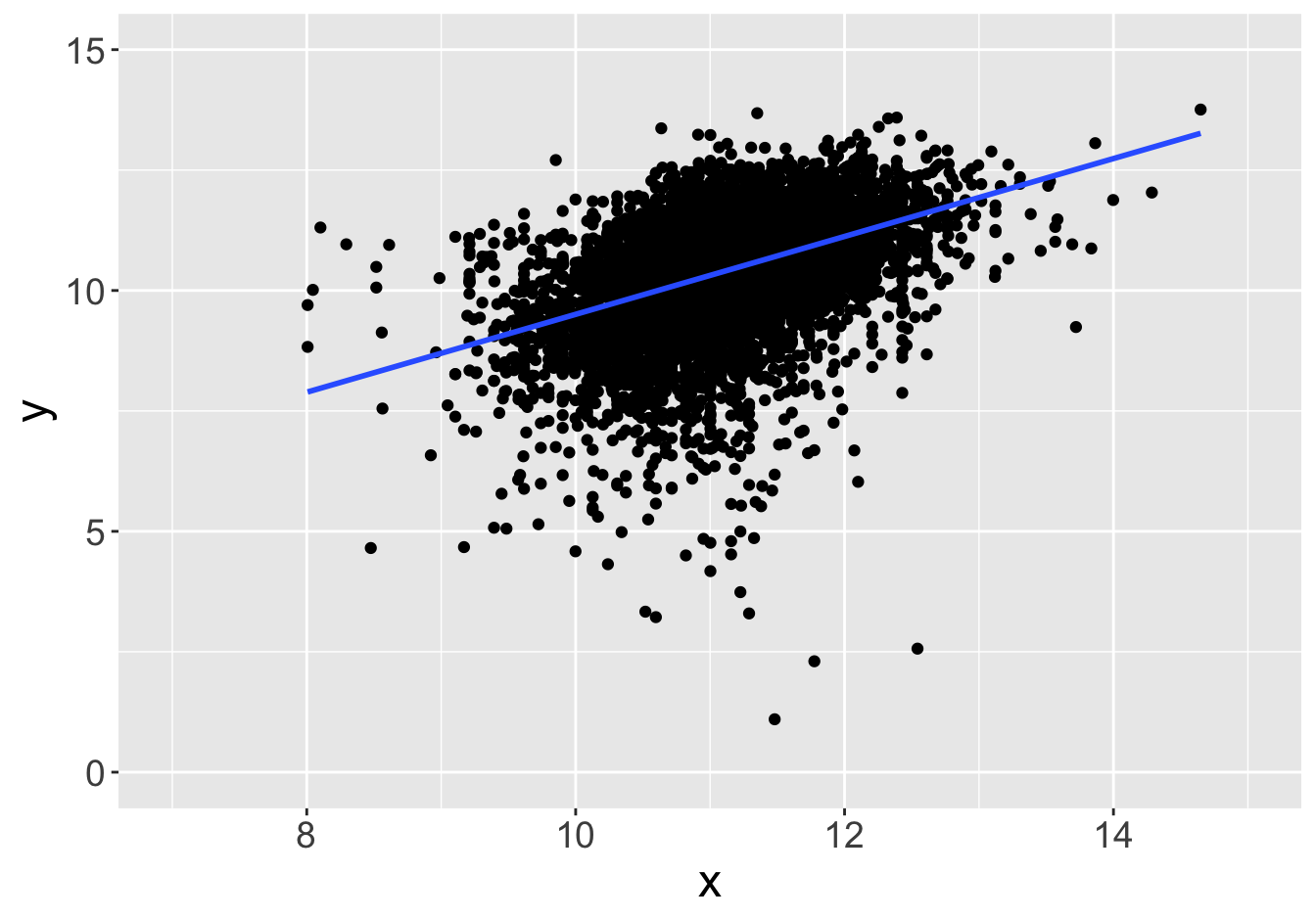
Example - Slopes (Sample Size 100)

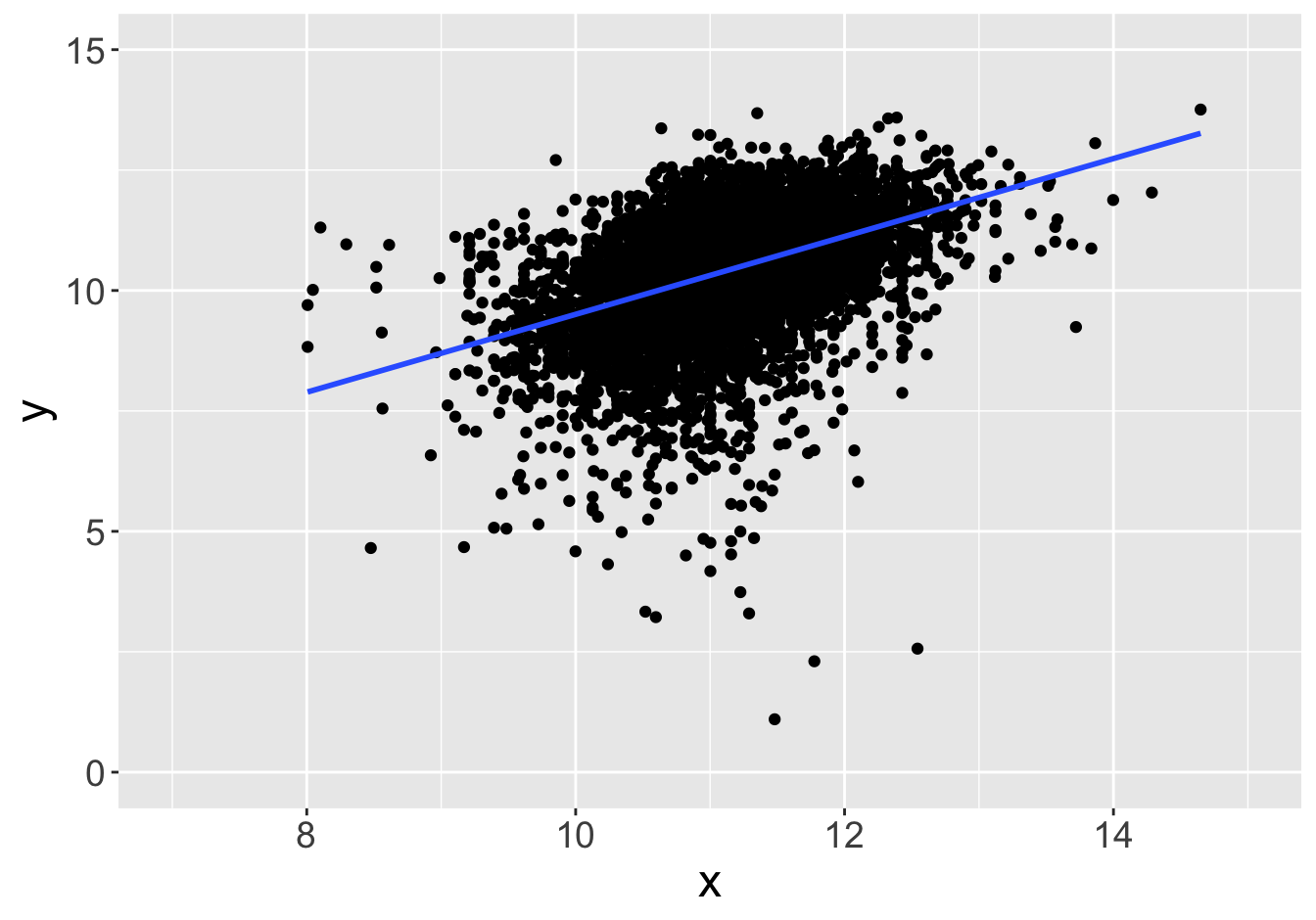
Slope: 0.81

Slope: 0.68

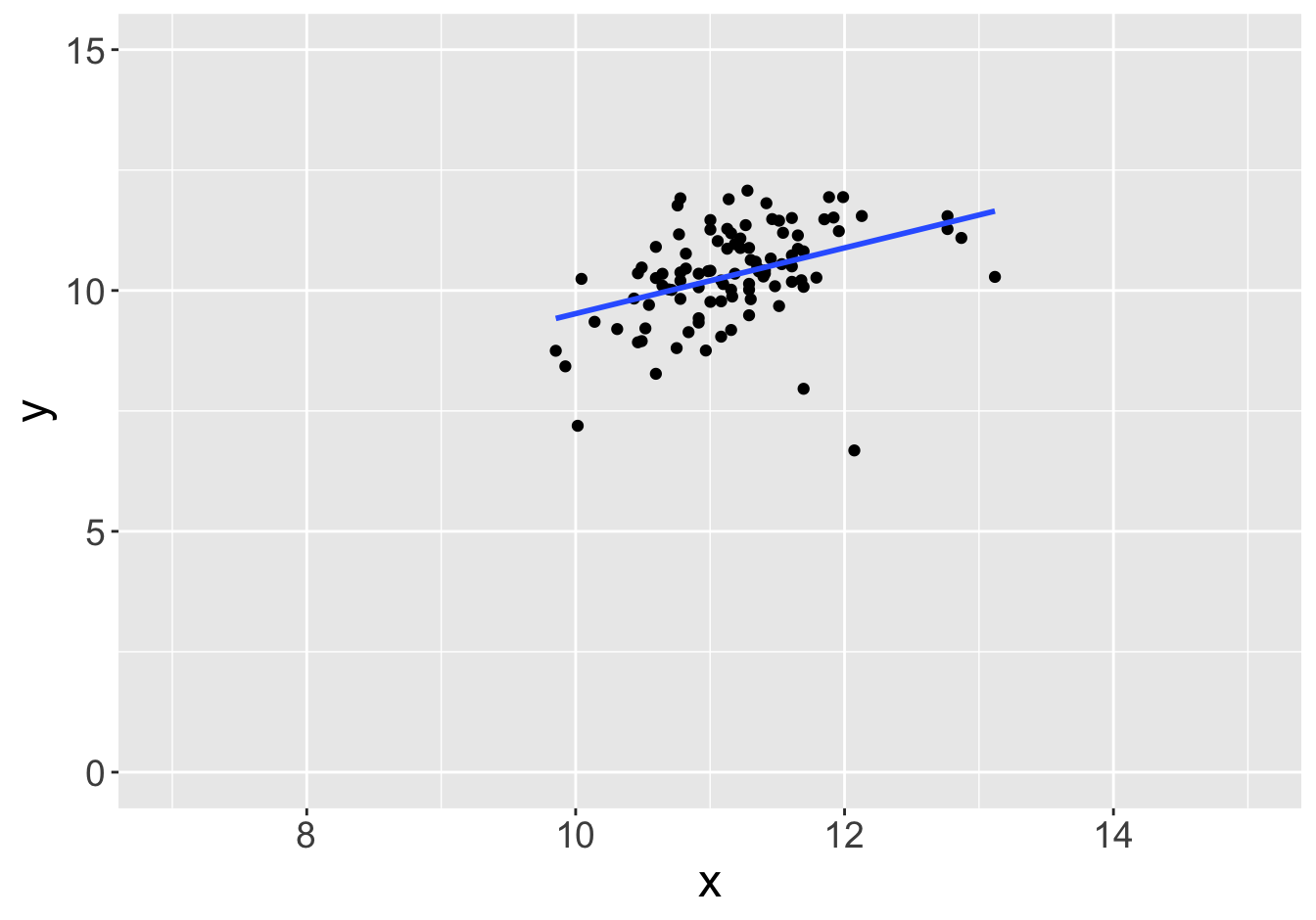
Example - Slopes (Sample Size 100)

Slope: 0.81

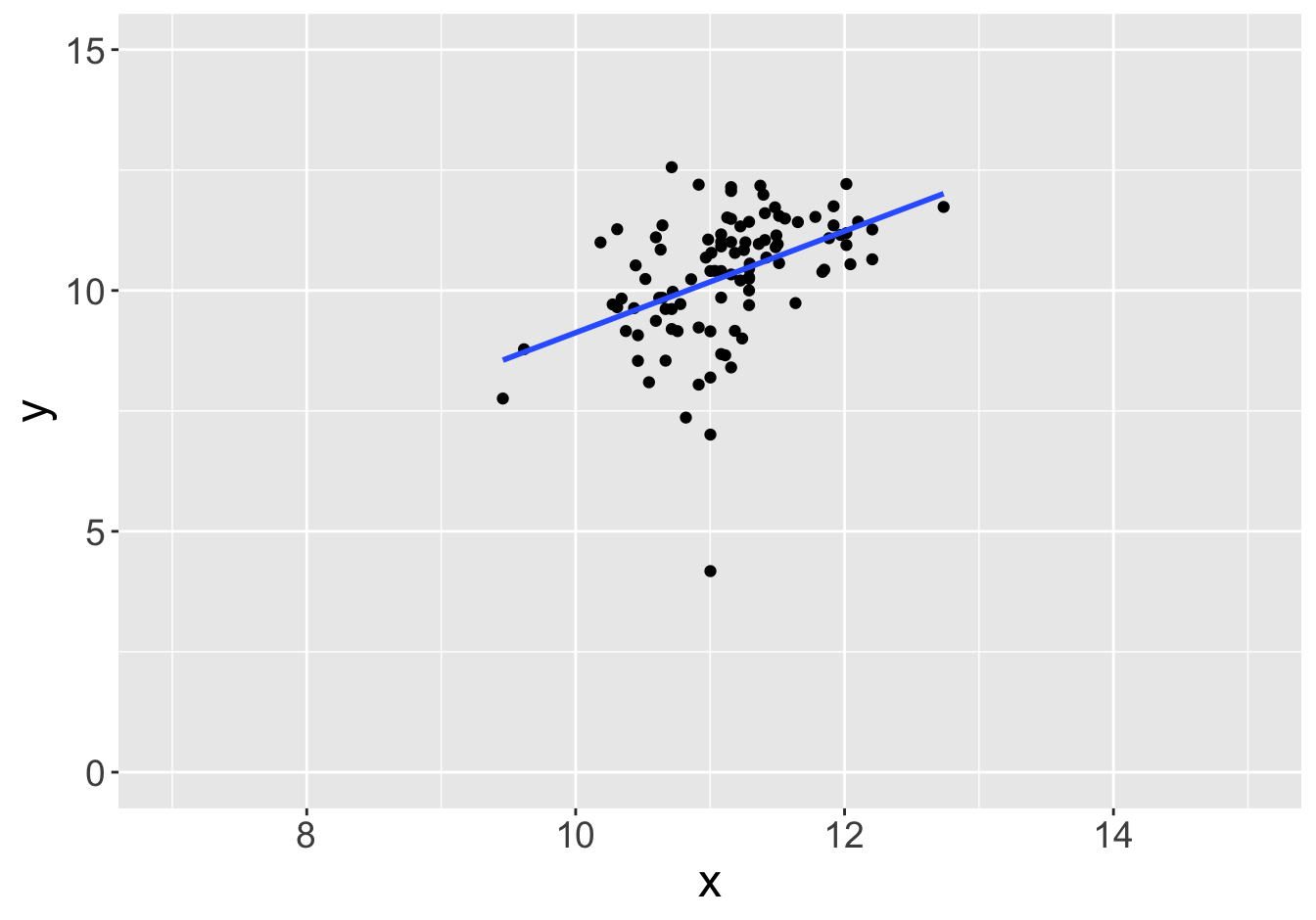
Slope: 1.05

Example - Slopes (Sample Size 100)

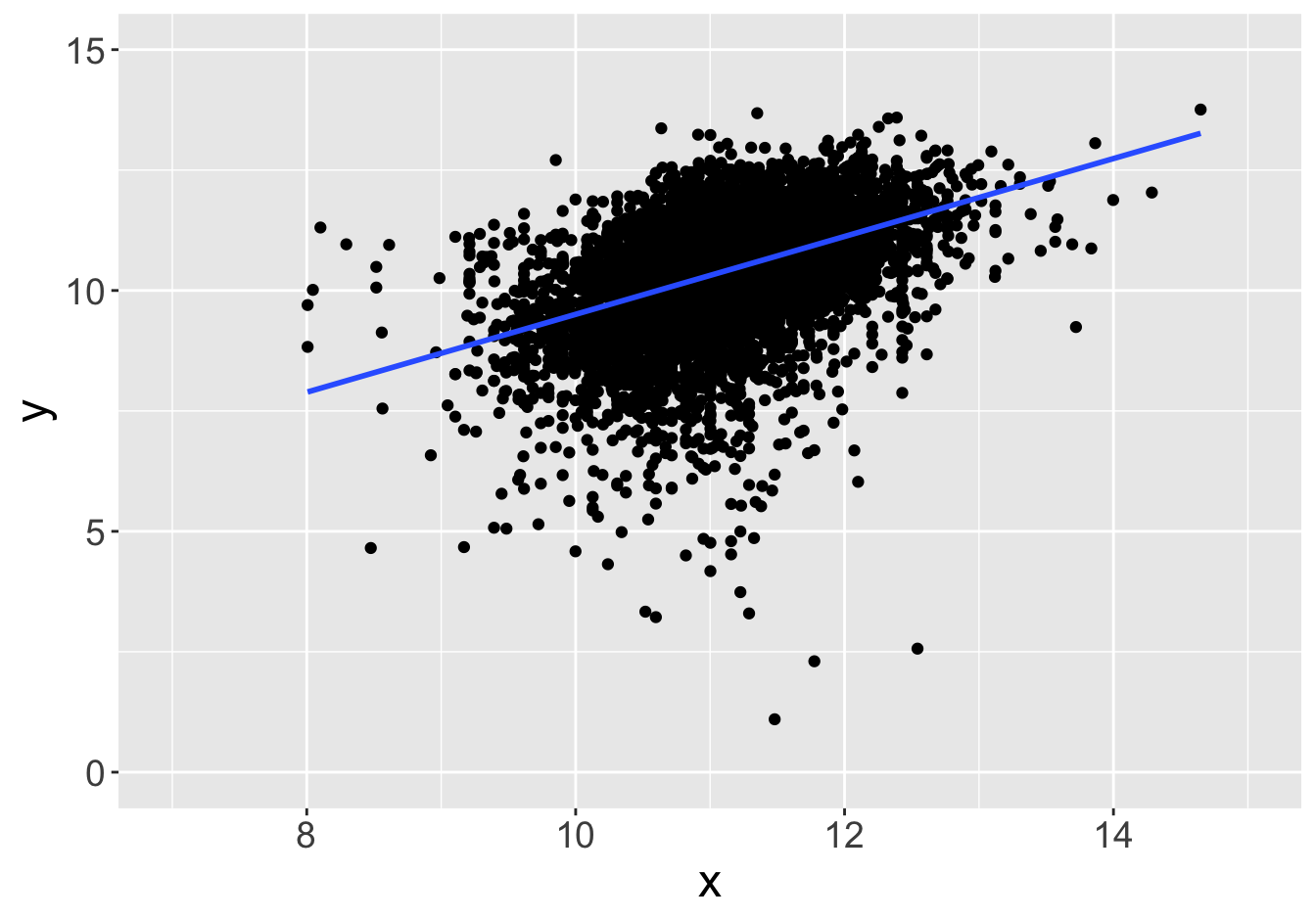
Slope: 0.81

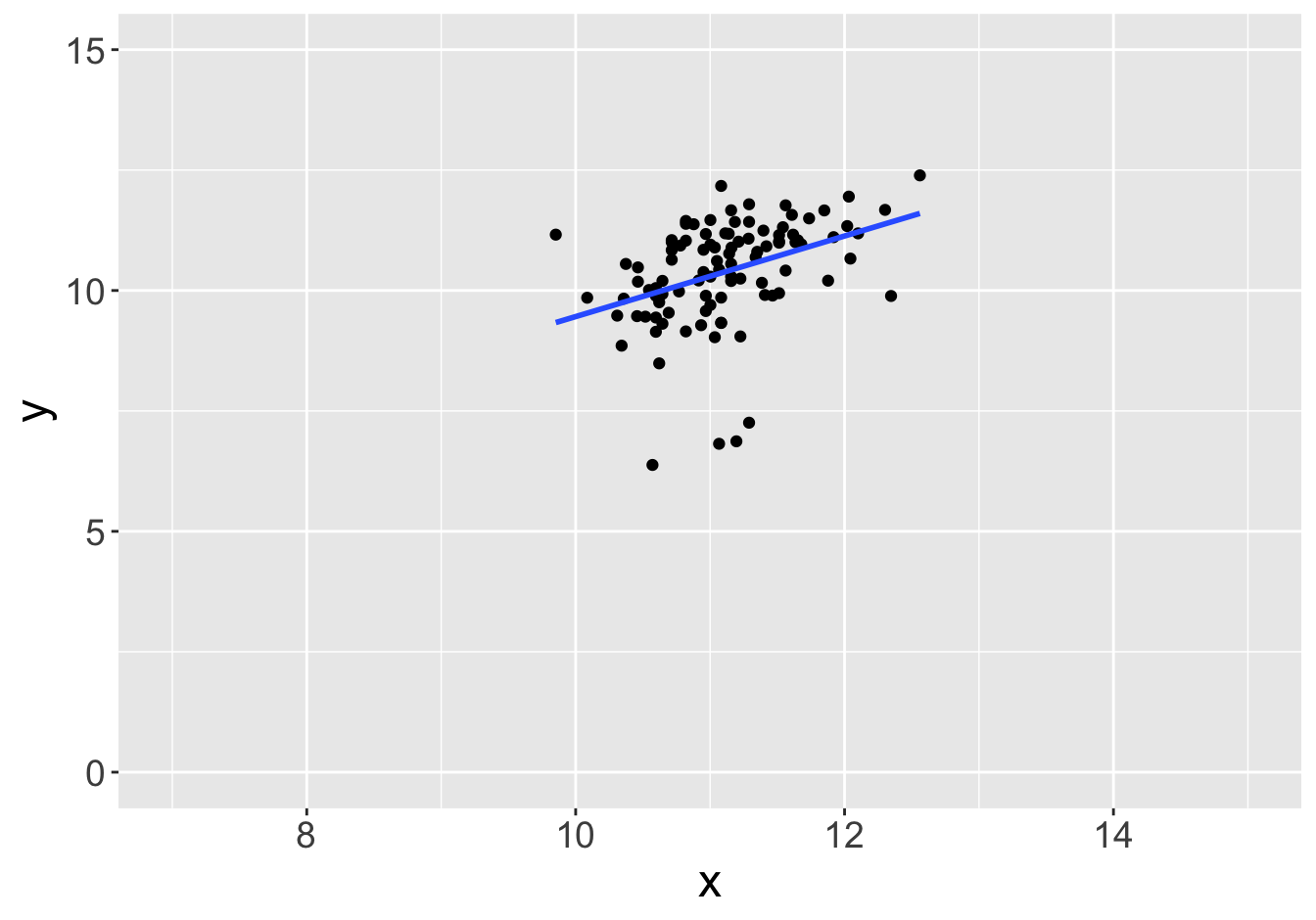
Slope: 0.84

Example - Slopes (Sample Size 100)

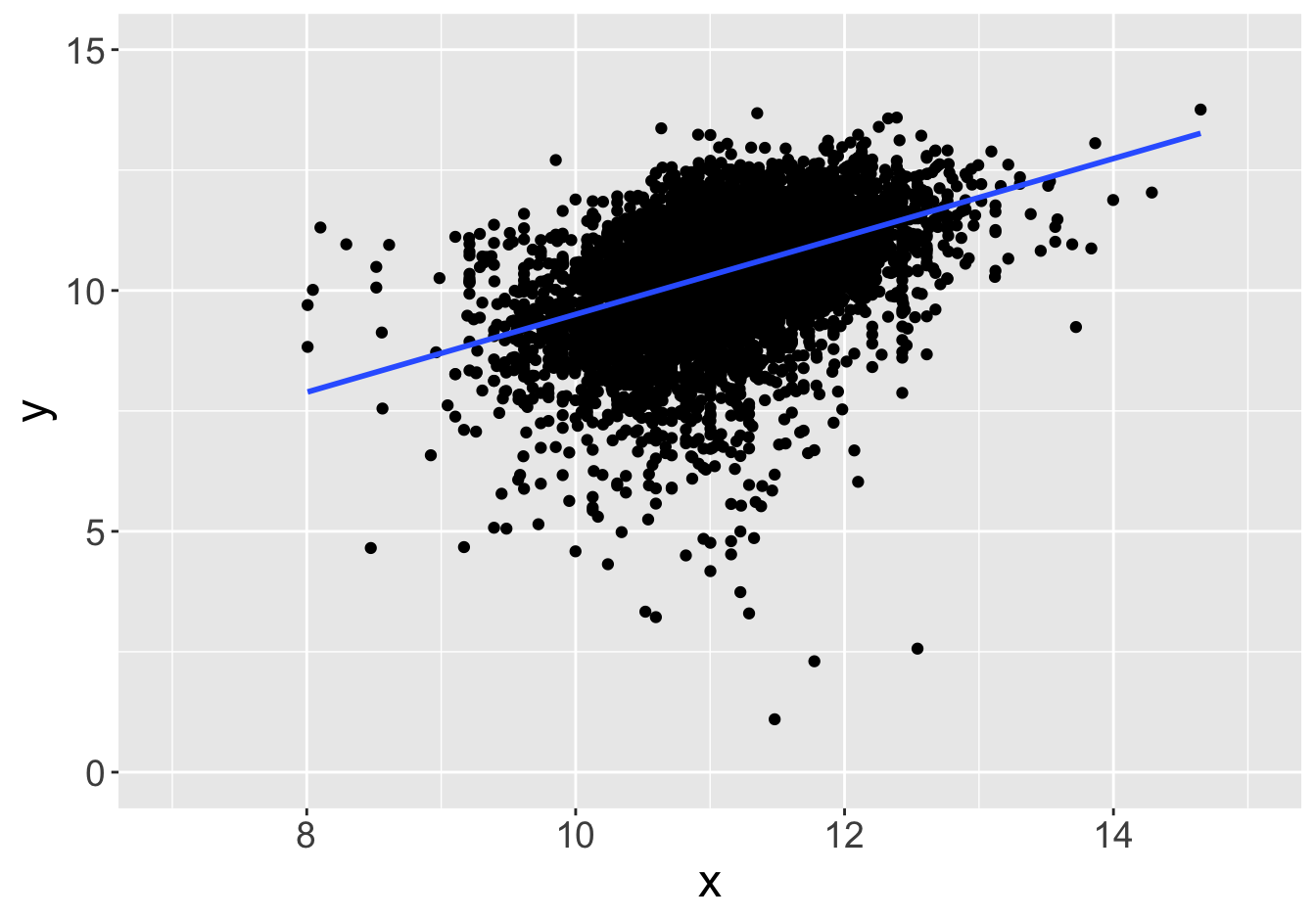
Slope: 0.81

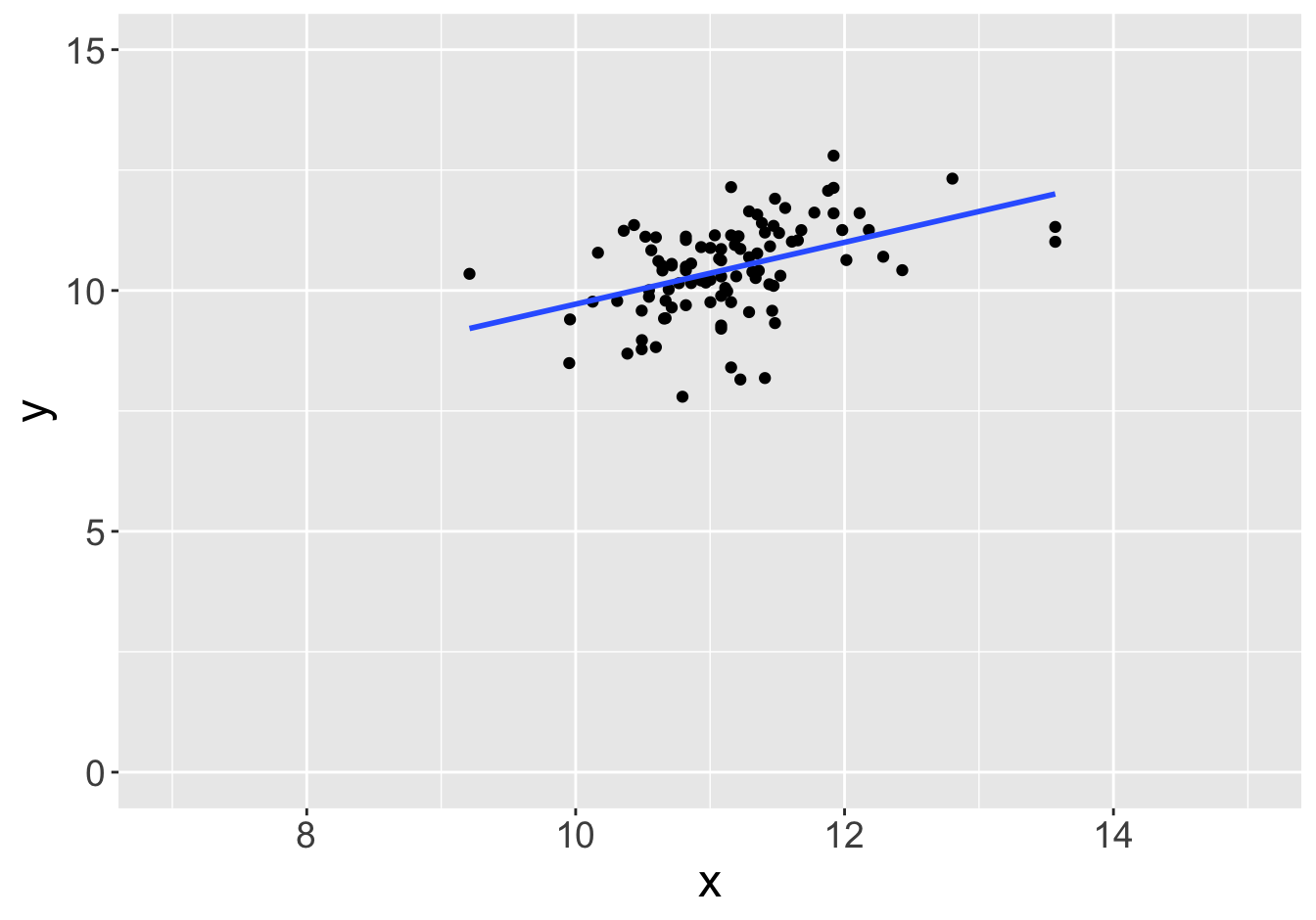
Slope: 0.64

Example - Slopes (Sample Size 1000)

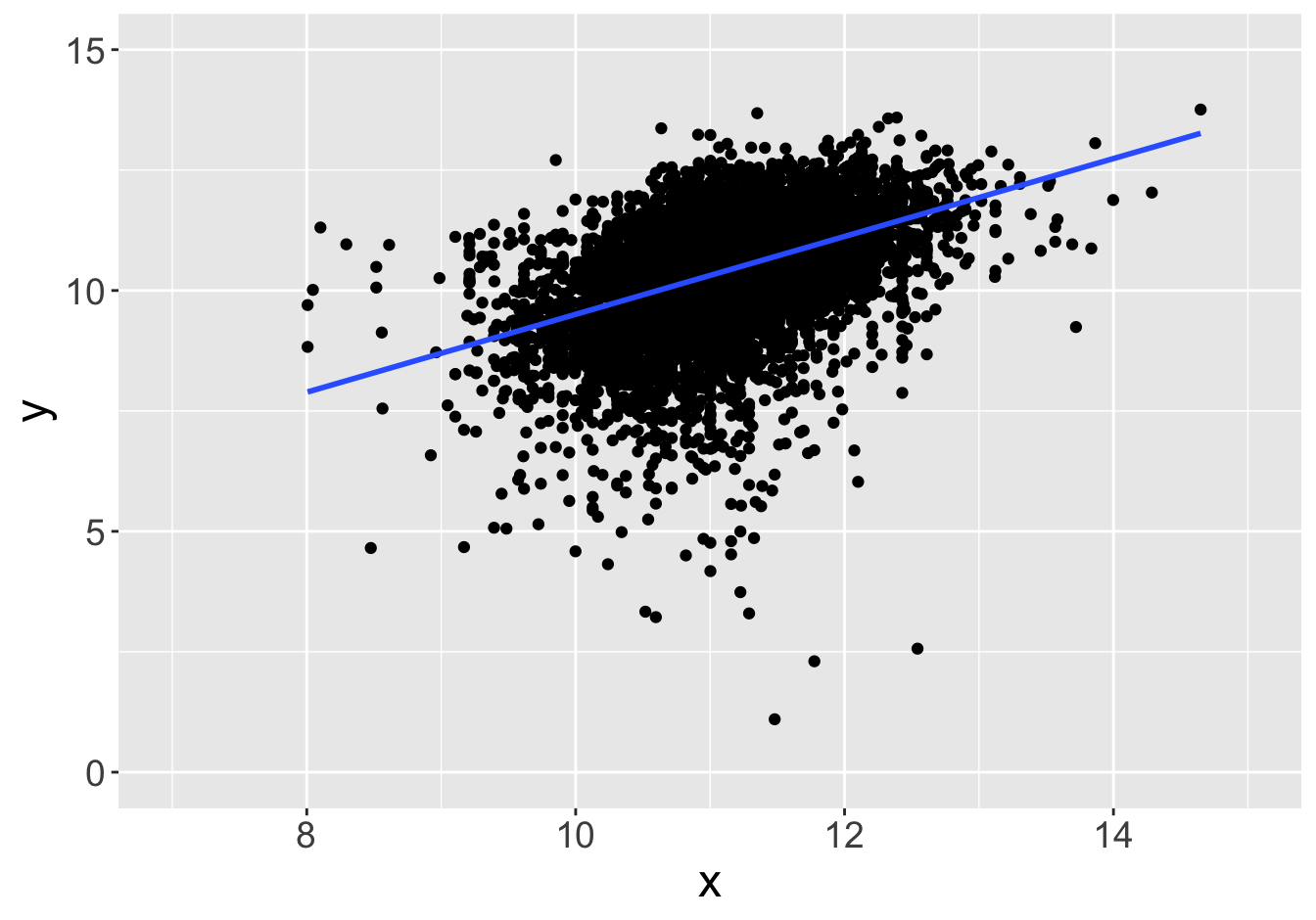
Slope: 0.81

Slope: 0.77

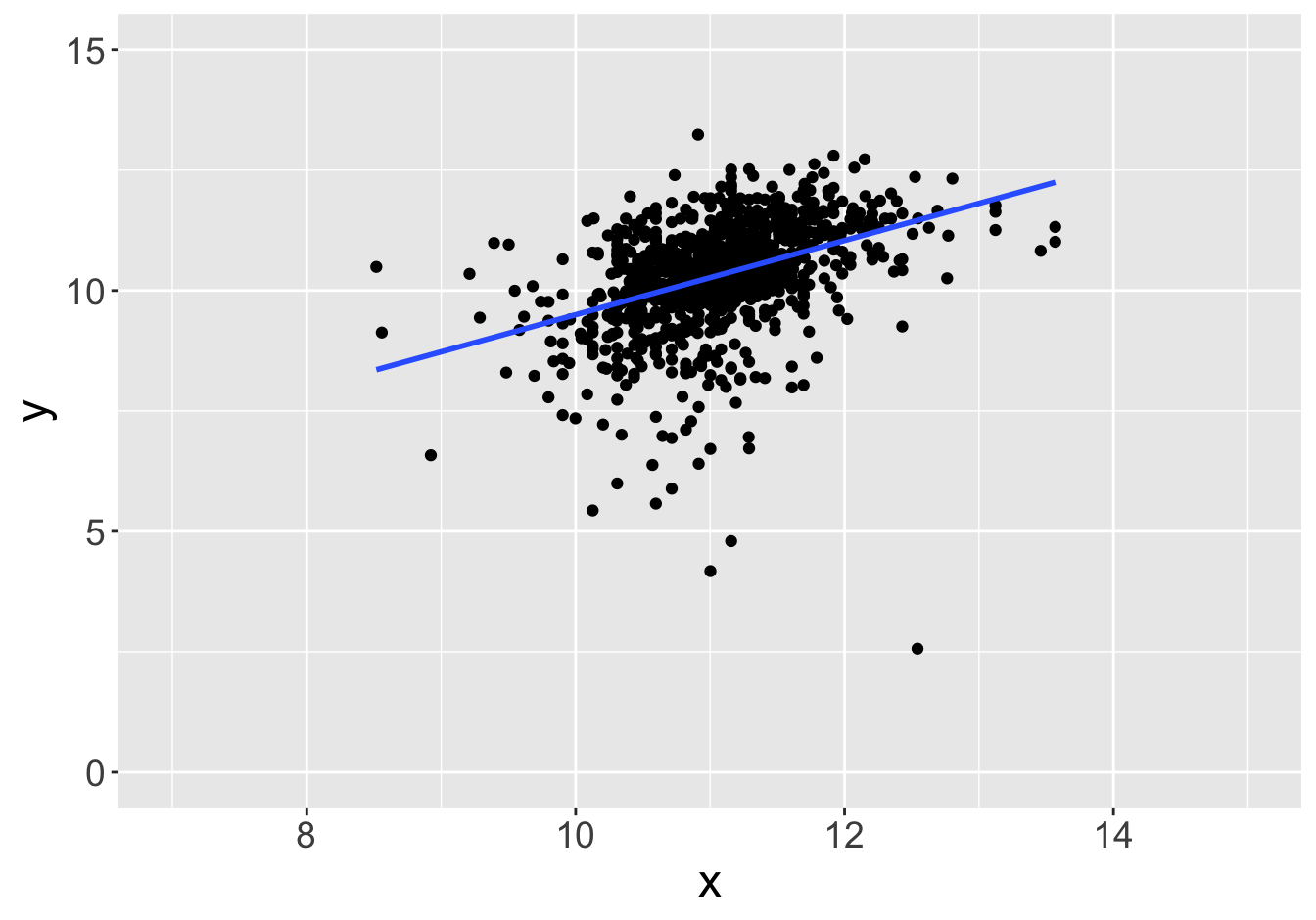
Example - Slopes (Sample Size 1000)

Slope: 0.81

Slope: 0.72

Example - Slopes (Sample Size 1000)

Slope: 0.81

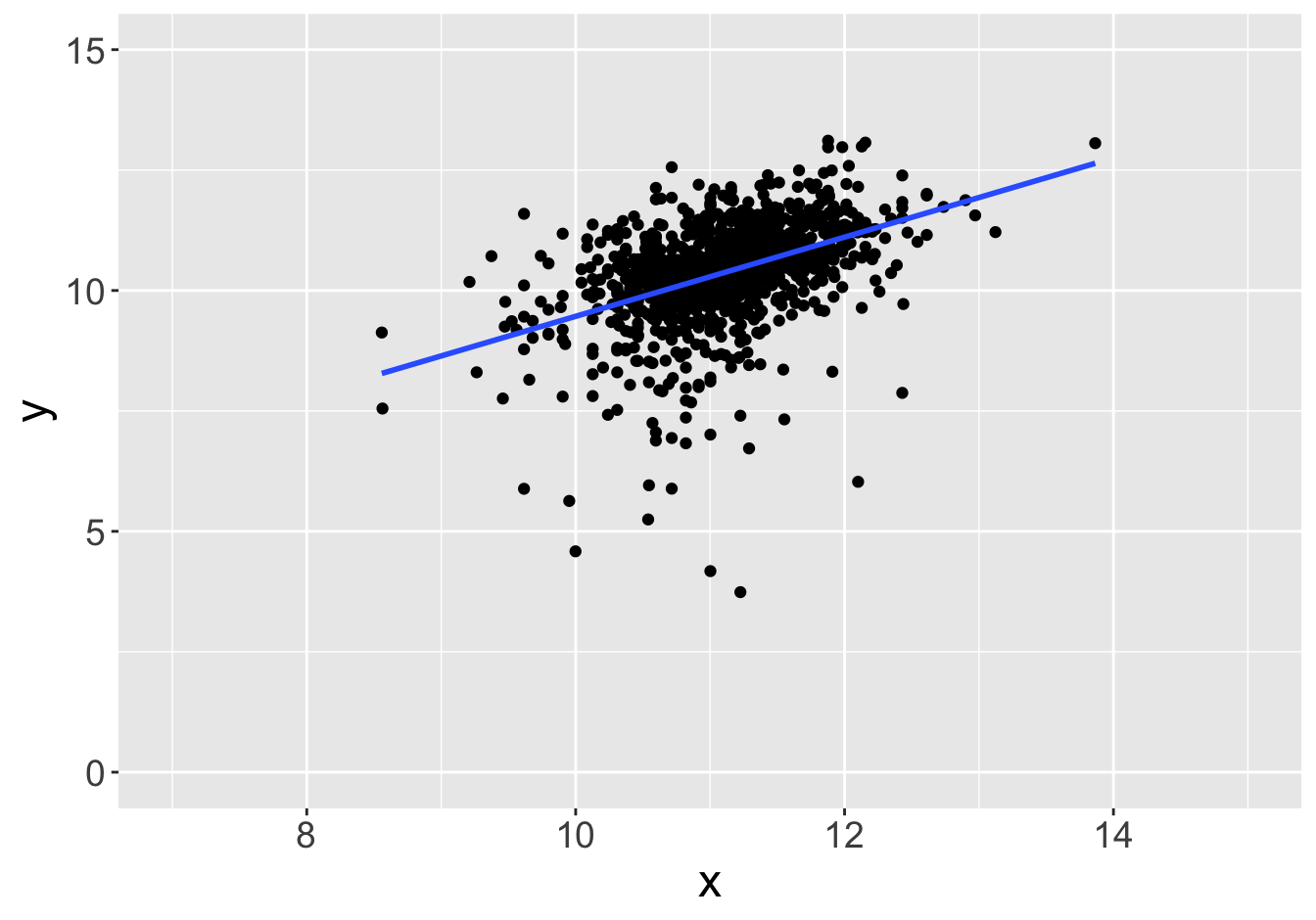
Slope: 0.82

Example - Slopes

How confident would you feel stating that the population slope is equal to any of these values?s

The Vision

How can we give a range of reasonable values for the population data using the sample data we have??

• Idea: use the sample to take more samples???

• Method: bootstrapping!

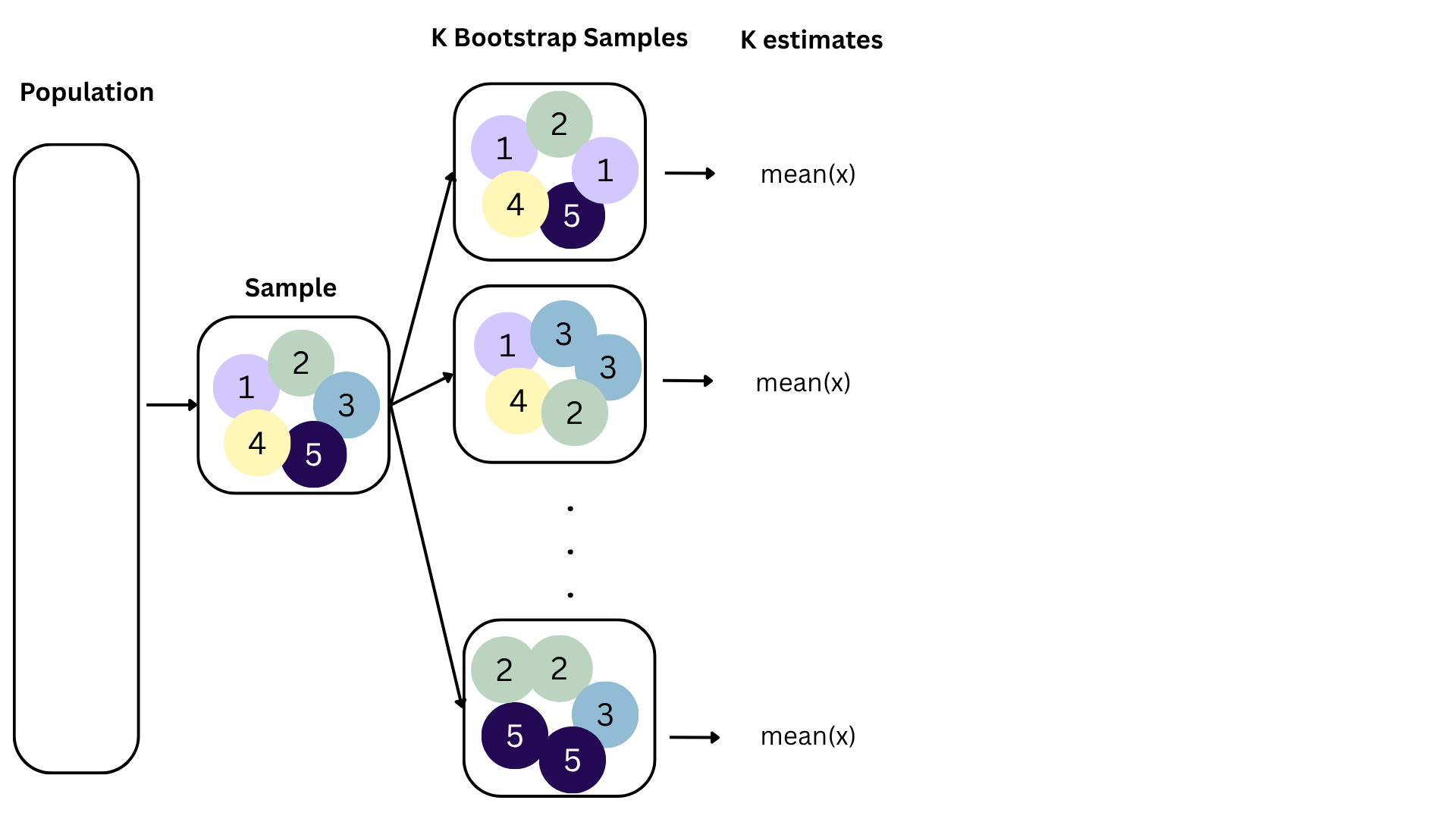
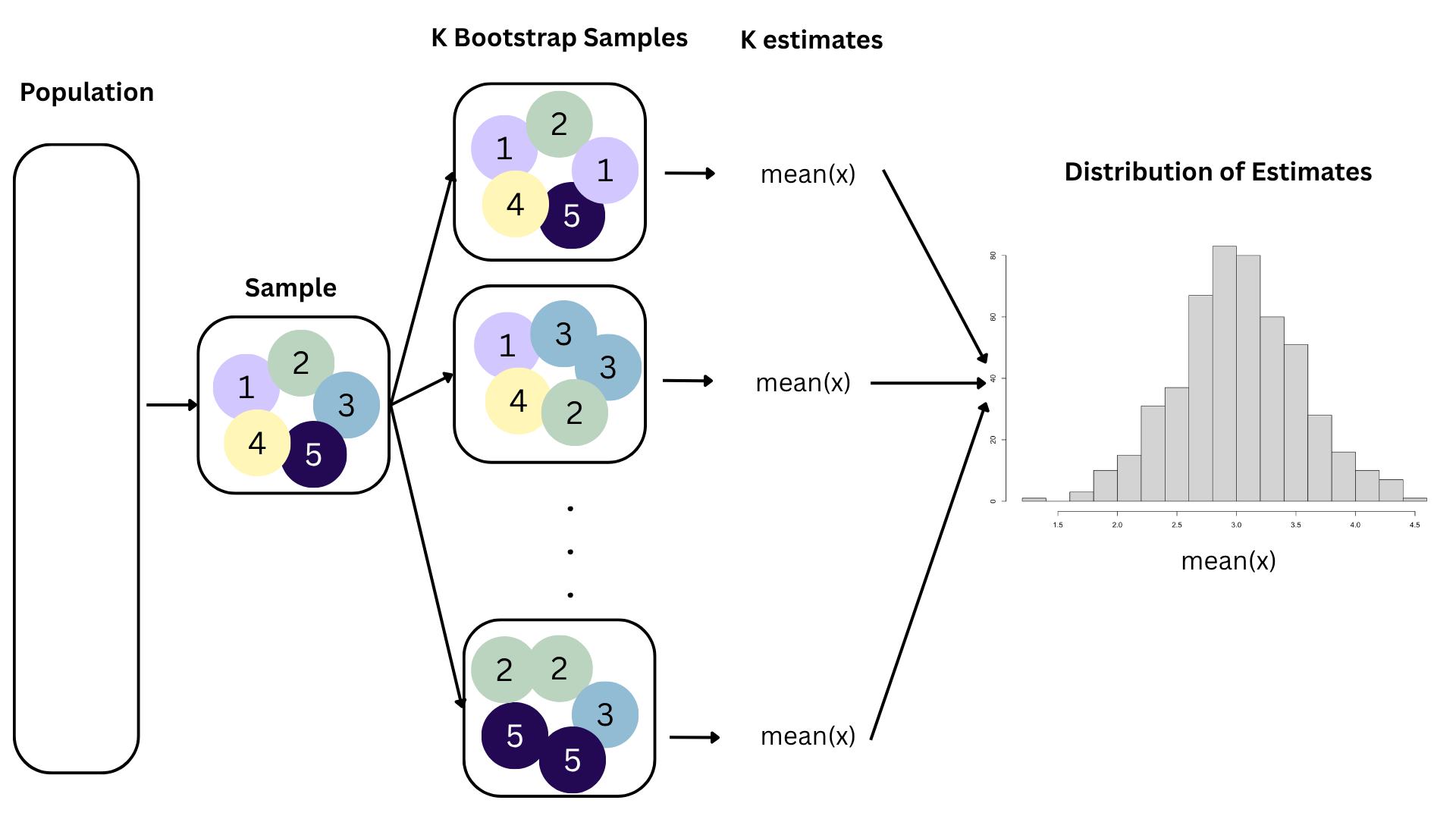
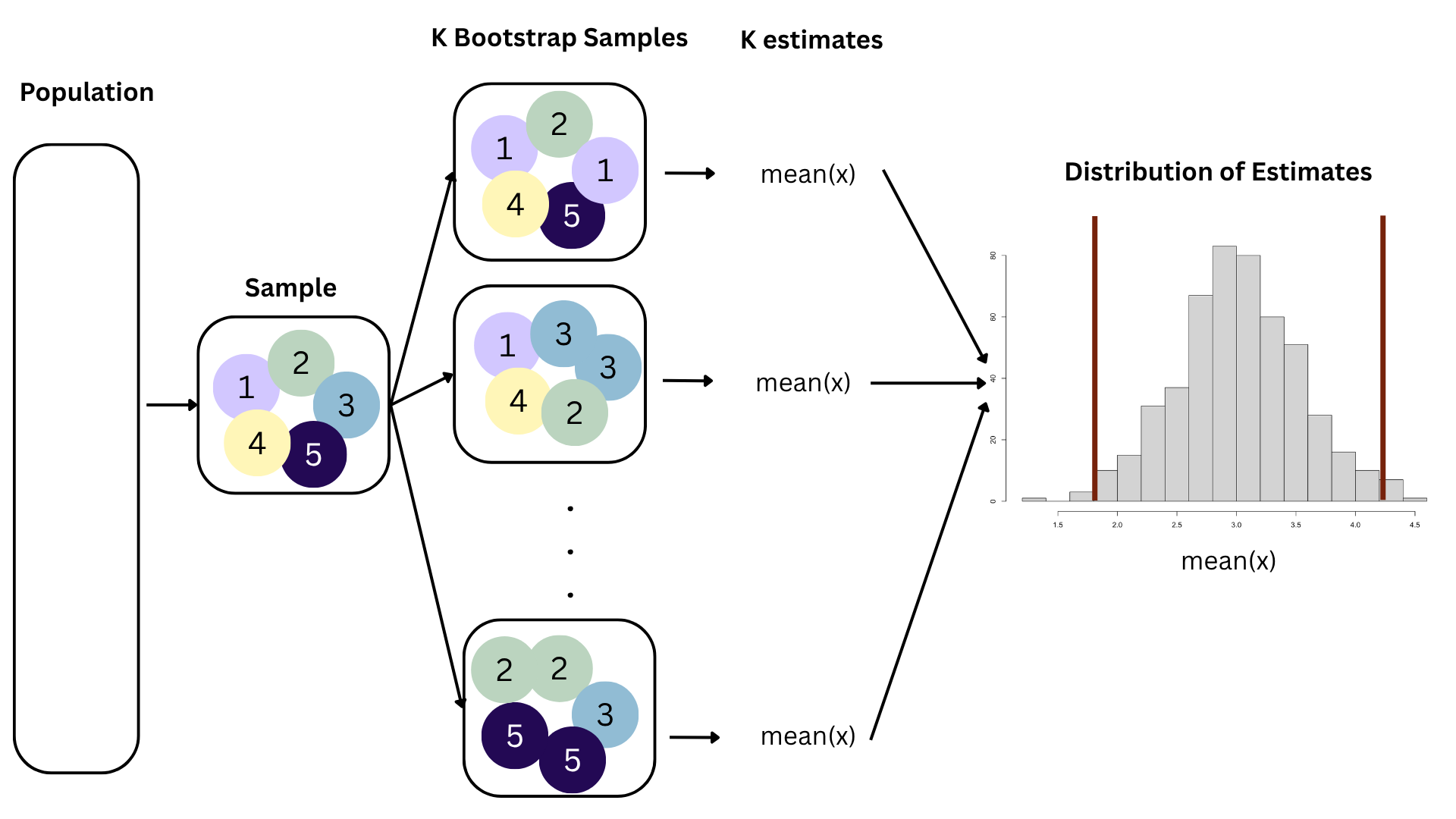
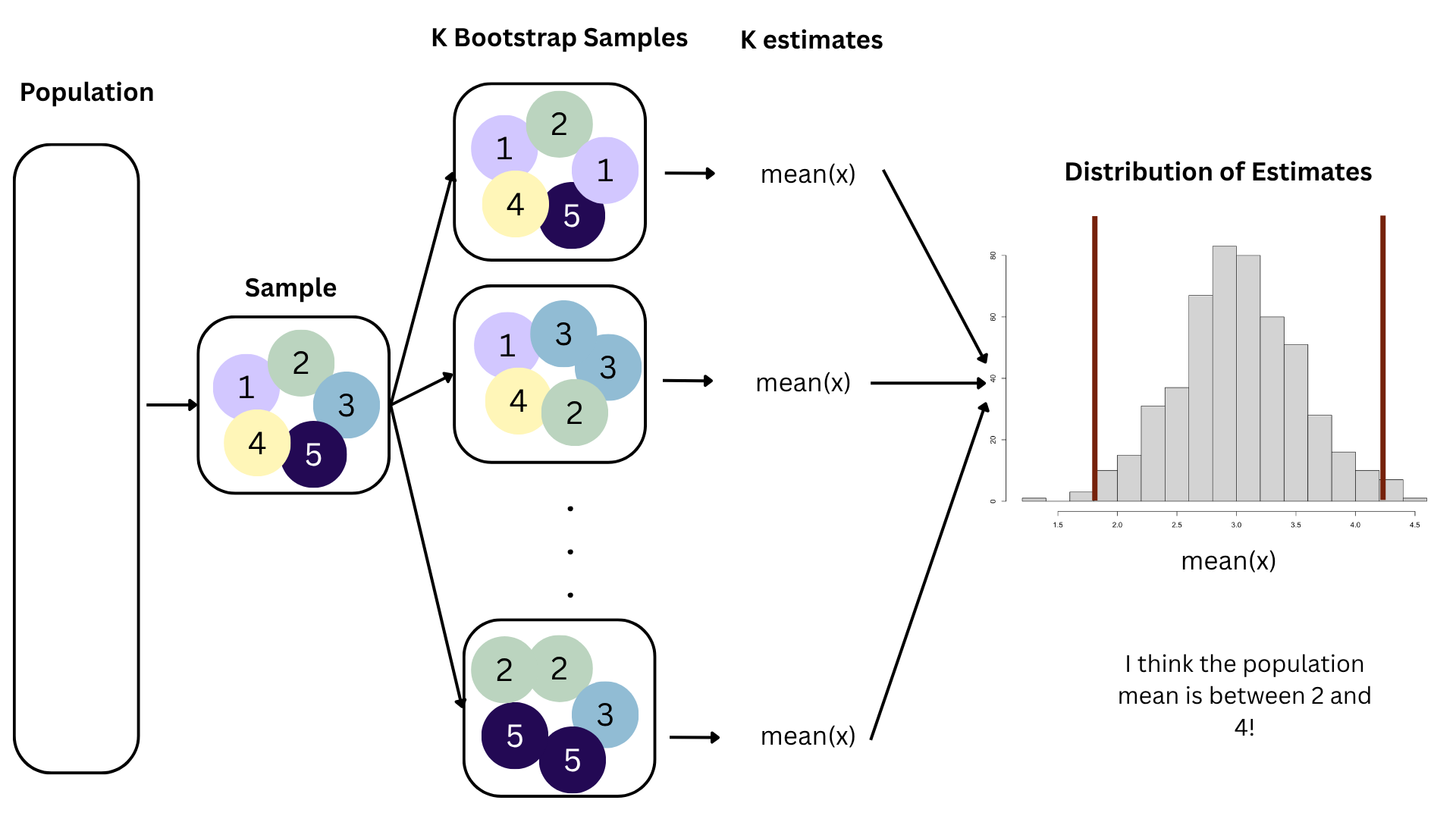
Bootstrapping

Bootstrapping

Bootstrapping

Bootstrapping

Bootstrapping

Bootstrapping

Bootstrapping

Today’s Goal

Find range of plausible values for a slope using bootstrap confidence intervals.

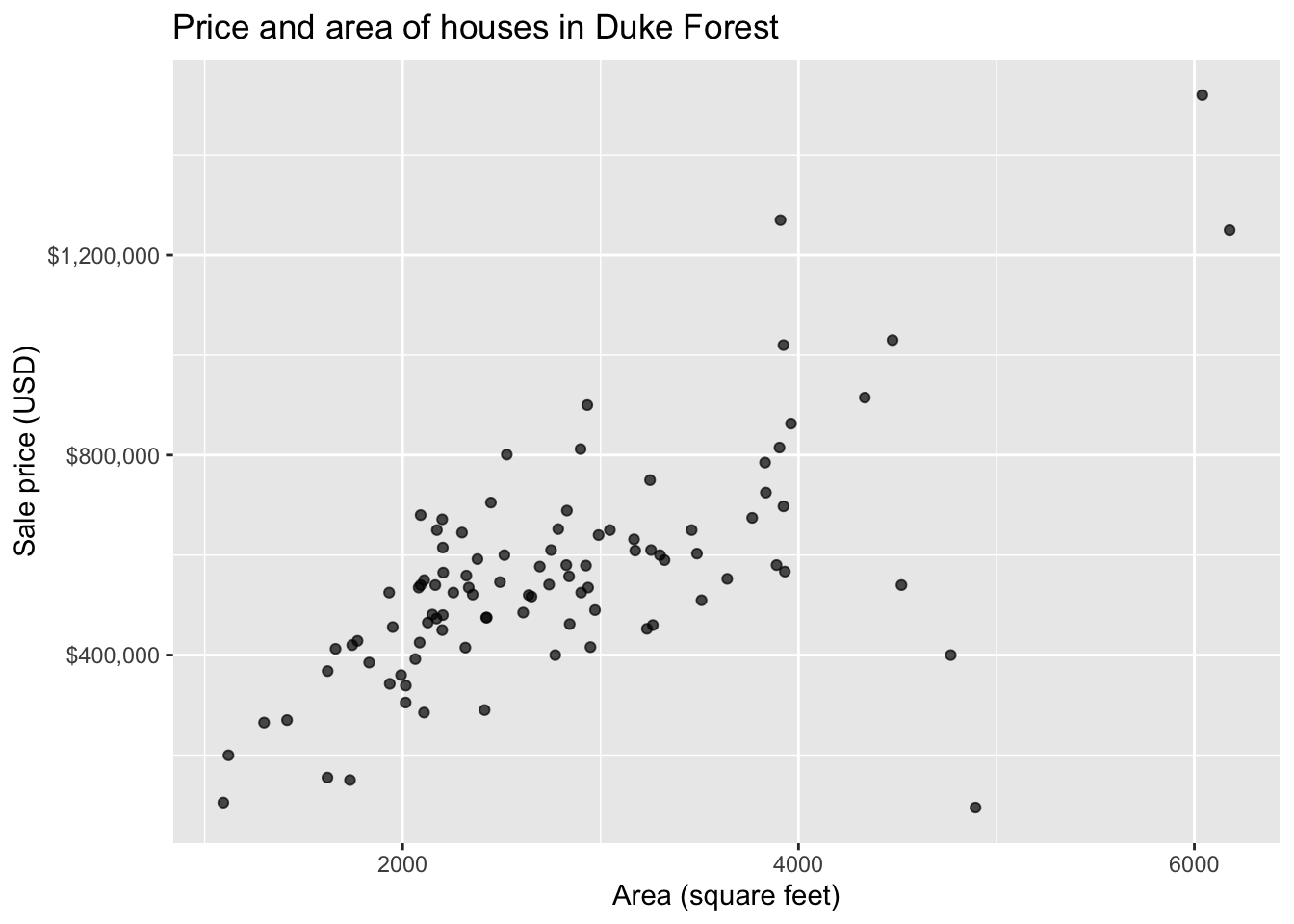
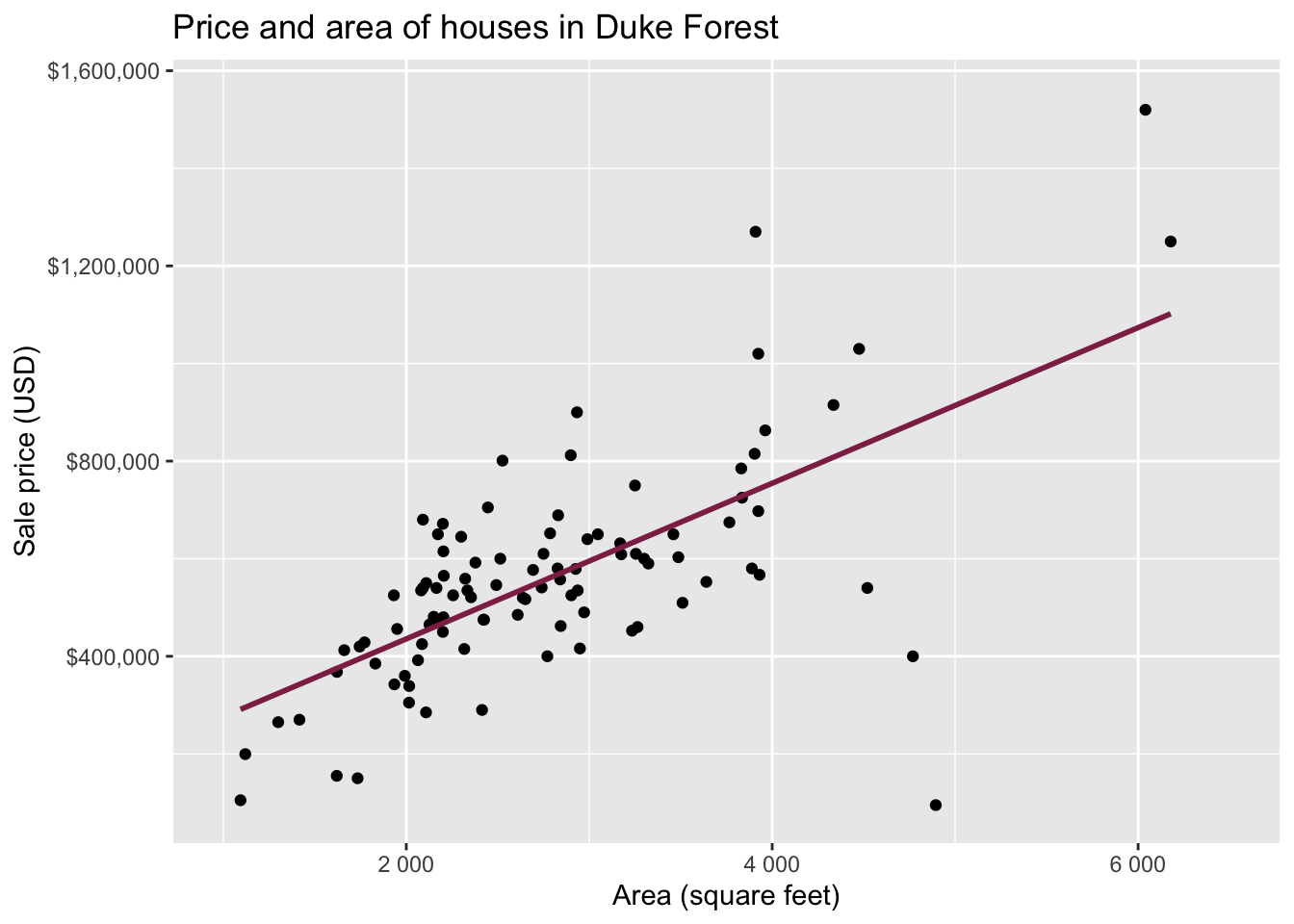
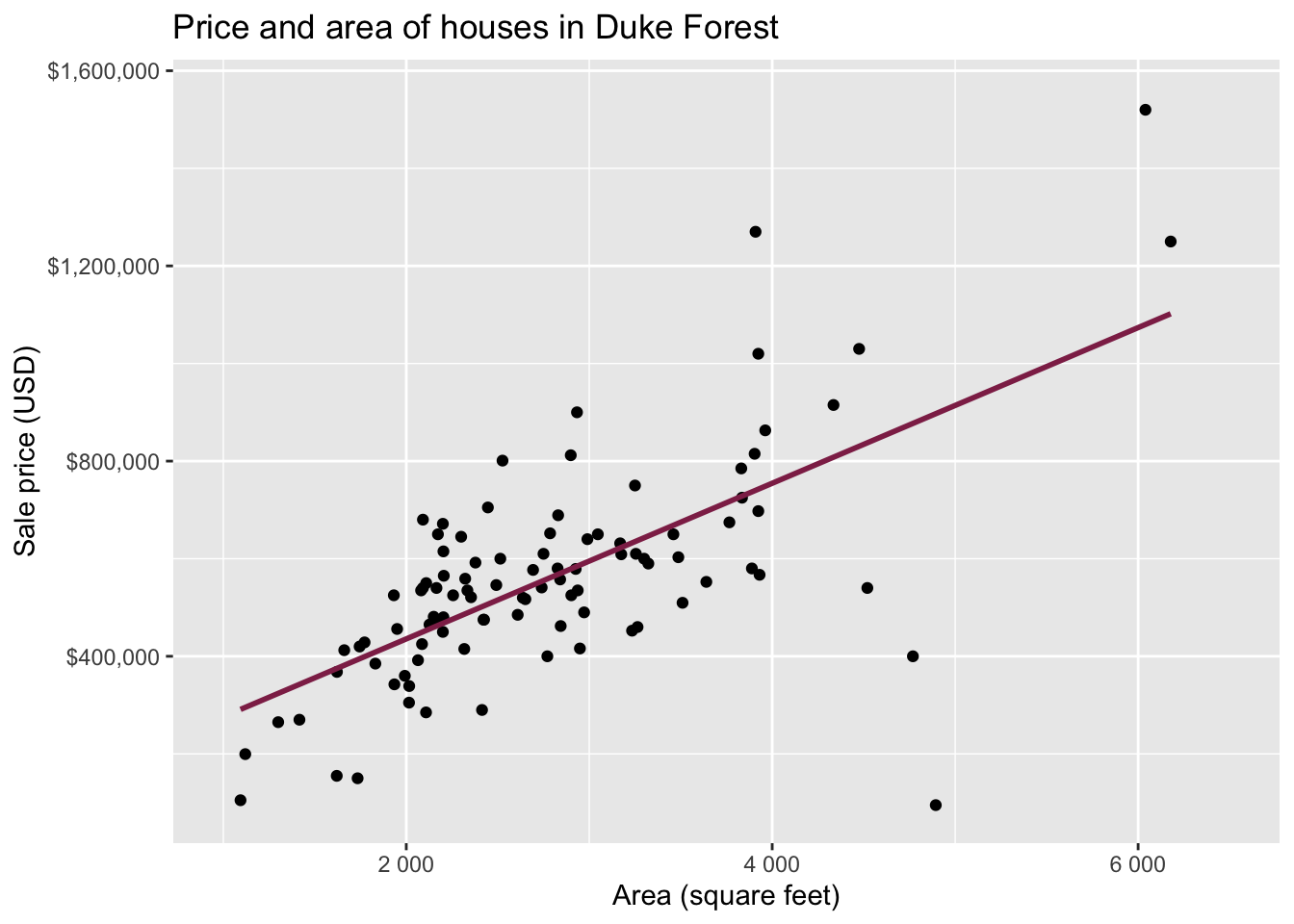
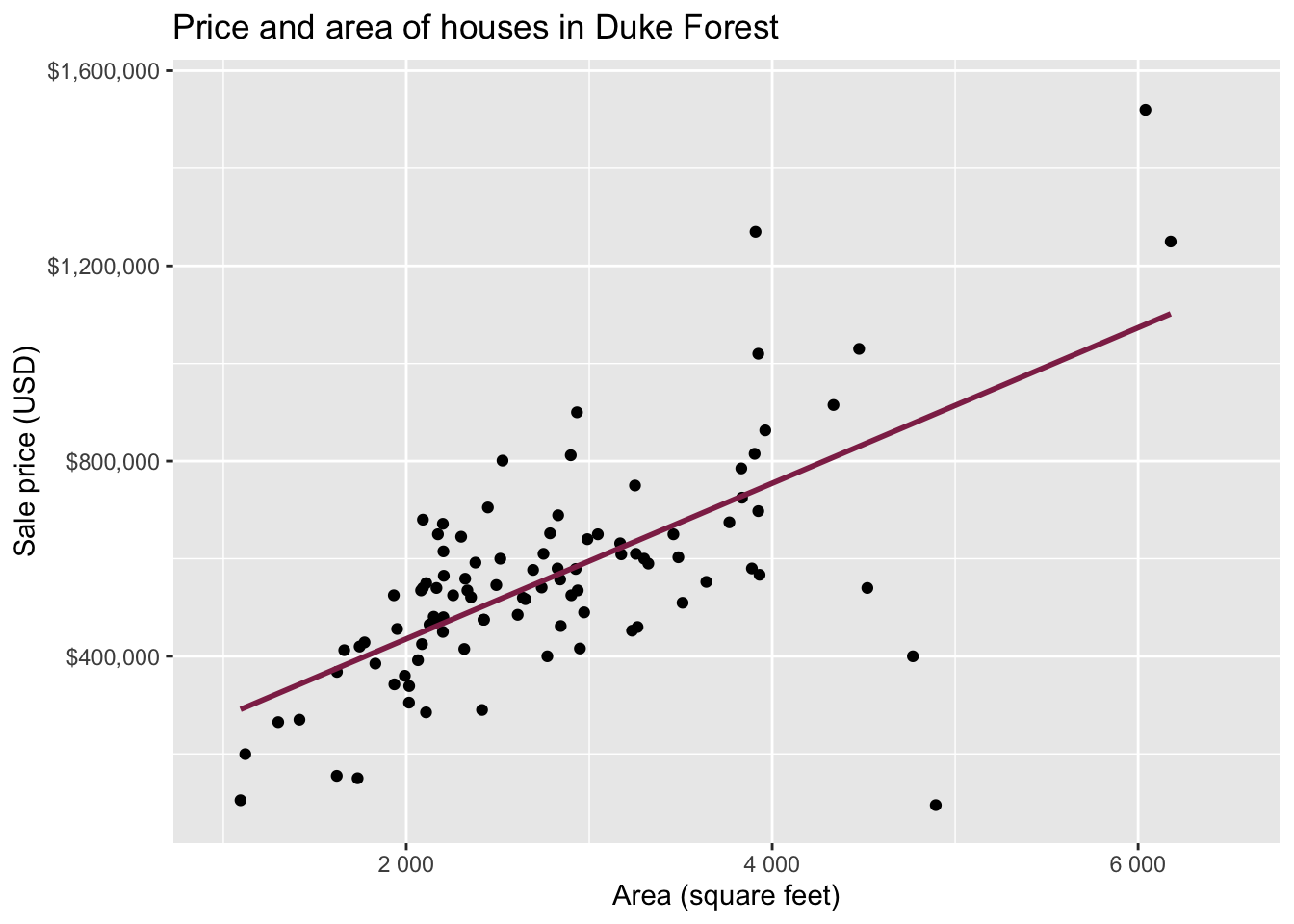
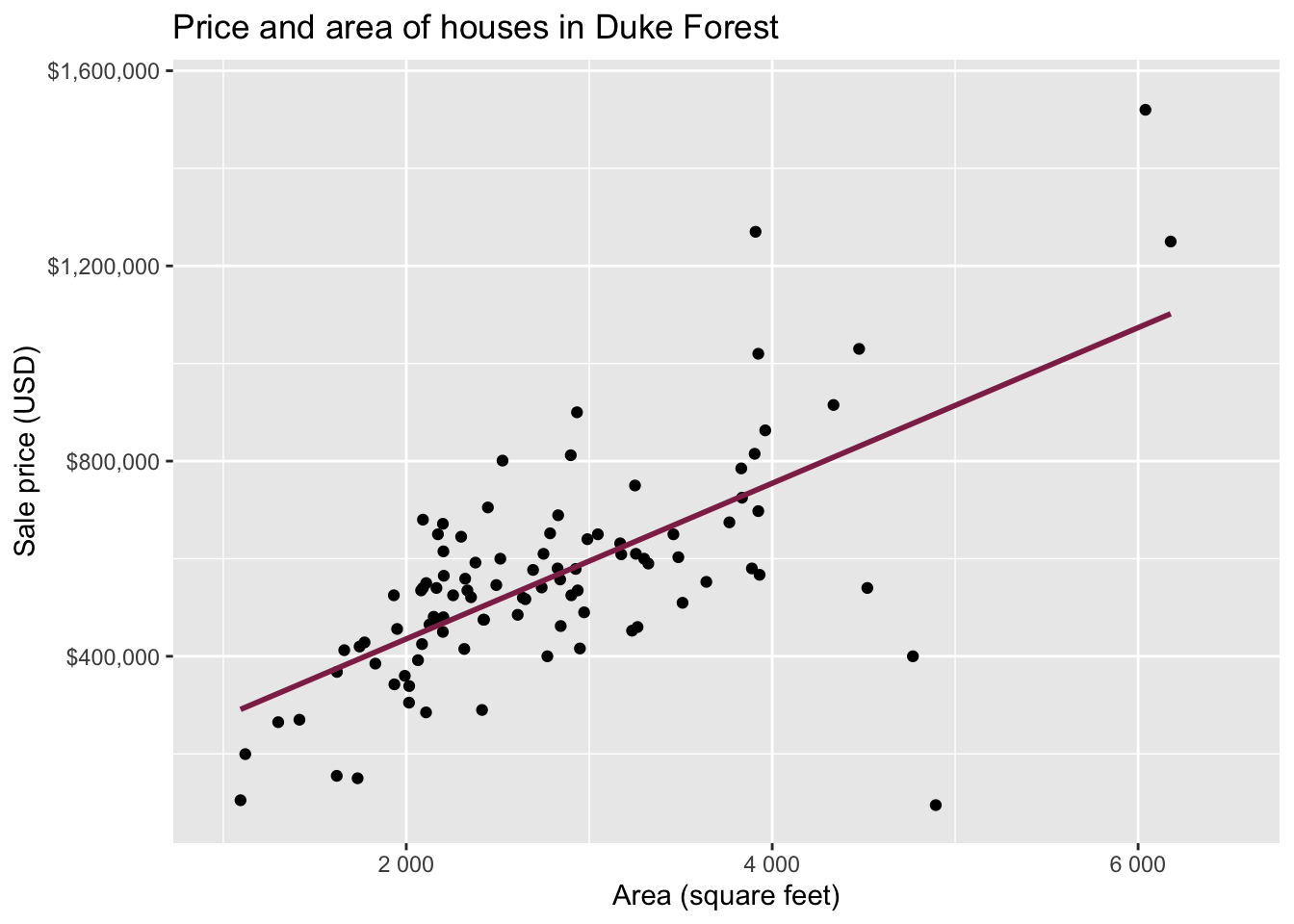
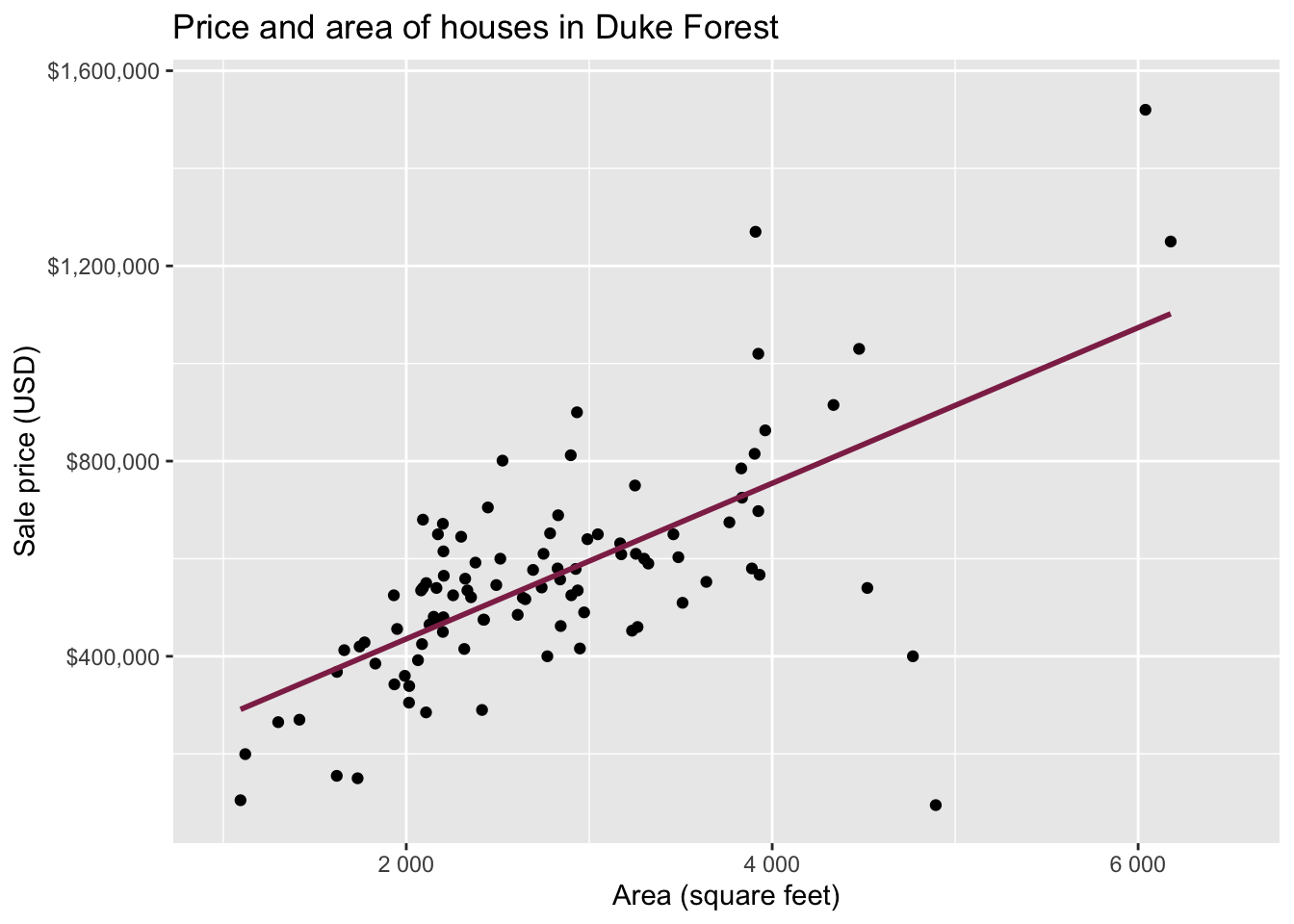
Data: Houses in Duke Forest

• Data on houses that were sold in the Duke Forest neighborhood of Durham, NC around November 2020
• Pulled from Zillow
• Source: openintro::duke_forest

Goal: Use the area (in square feet) to understand variability in the price of houses in Duke Forest.

Exploratory data analysis

ggplot(duke_forest, aes(x = area, y = price)) +
  geom_point(alpha = 0.7) +
  labs(
    x = "Area (square feet)",
    y = "Sale price (USD)",
    title = "Price and area of houses in Duke Forest"
  ) +
  scale_y_continuous(labels = label_dollar()) 

Modeling

df_fit <- linear_reg() |>
  fit(price ~ area, data = duke_forest)

tidy(df_fit) 

# A tibble: 2 × 5
  term        estimate std.error statistic  p.value
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)  116652.   53302.       2.19 3.11e- 2
2 area            159.      18.2      8.78 6.29e-14

• Intercept: Duke Forest houses that are 0 square feet are expected to sell, for $116,652, on average.

• Slope: For each additional square foot, we expect the sale price of Duke Forest houses to be higher by $159, on average.

From sample to population

For each additional square foot, we expect the sale price of Duke Forest houses to be higher by $159, on average.

• This estimate is valid for the single sample of 98 houses.
• But what if we’re not interested quantifying the relationship between the size and price of a house in this single sample?
• What if we want to say something about the relationship between these variables for all houses in Duke Forest?

Inference for simple linear regression

• Calculate a confidence interval for the slope, \(\beta_1\) (today)

• Conduct a hypothesis test for the slope,\(\beta_1\) (next week)

Confidence interval for the slope

Confidence interval

• A plausible range of values for a population parameter is called a confidence interval
• Using only a single point estimate is like fishing in a murky lake with a spear. Using a confidence interval is like fishing with a net.
  • We can throw a spear where we saw a fish but we will probably miss. If we toss a net in that area, we have a good chance of catching the fish.
  • If we report a point estimate, we probably will not hit the exact population parameter. If we report a range of plausible values we have a good shot at capturing the parameter

Confidence interval for the slope

A confidence interval will allow us to make a statement like “For each additional square foot, the model predicts the sale price of Duke Forest houses to be higher, on average, by $159, plus or minus X dollars.”

• Should X be $10? $100? $1000?

• If we were to take another sample of 98 would we expect the slope calculated based on that sample to be exactly $159? Off by $10? $100? $1000?

• The answer depends on how variable (from one sample to another sample) the sample statistic (the slope) is

• We need a way to quantify the variability of the sample statistic

Quantify the variability of the slope

• Two approaches:
  1. Via simulation (what we’ll do in this course)
  2. Via mathematical models (what you can learn about in future courses)

Quantify the variability of the slope

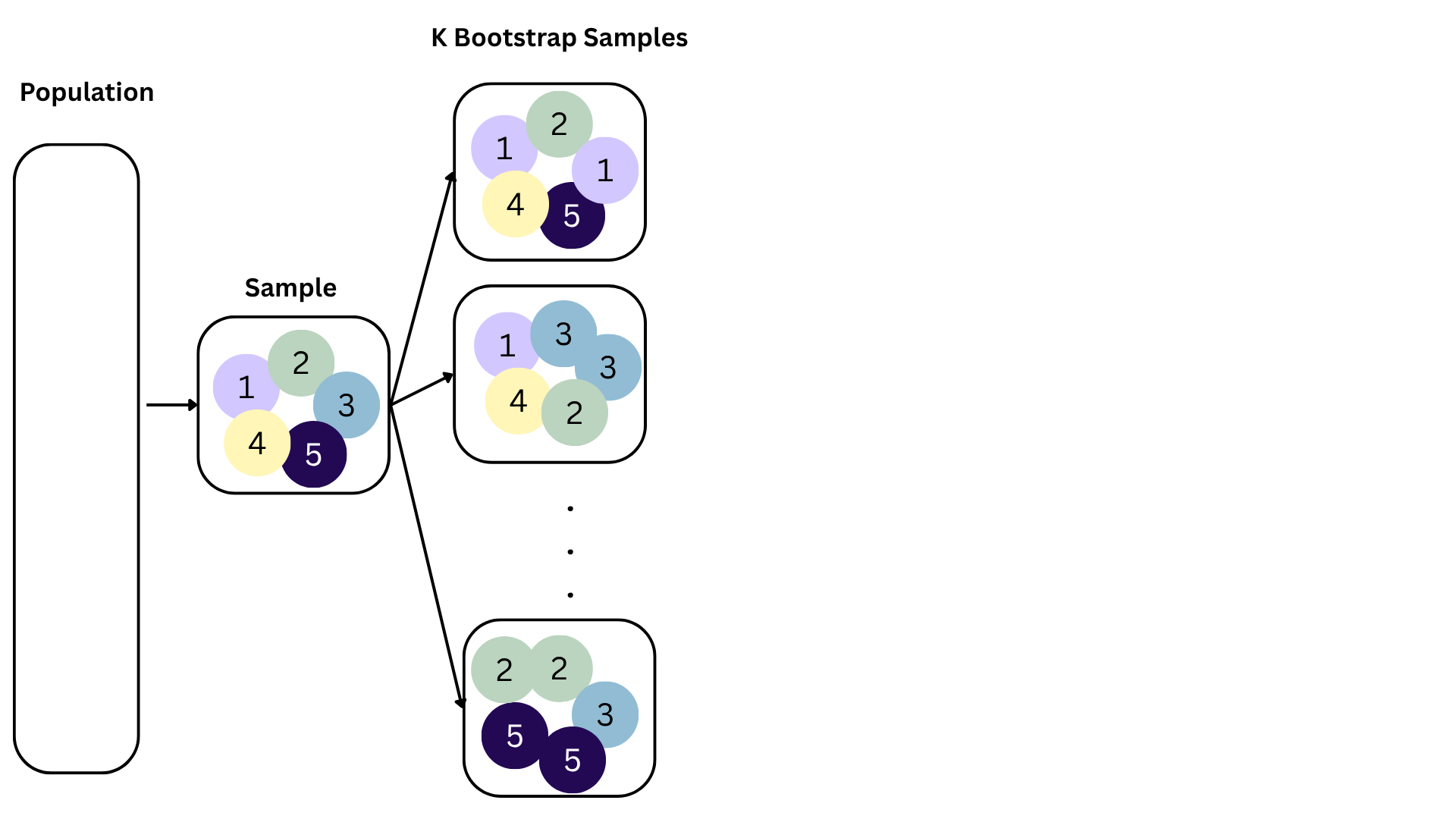
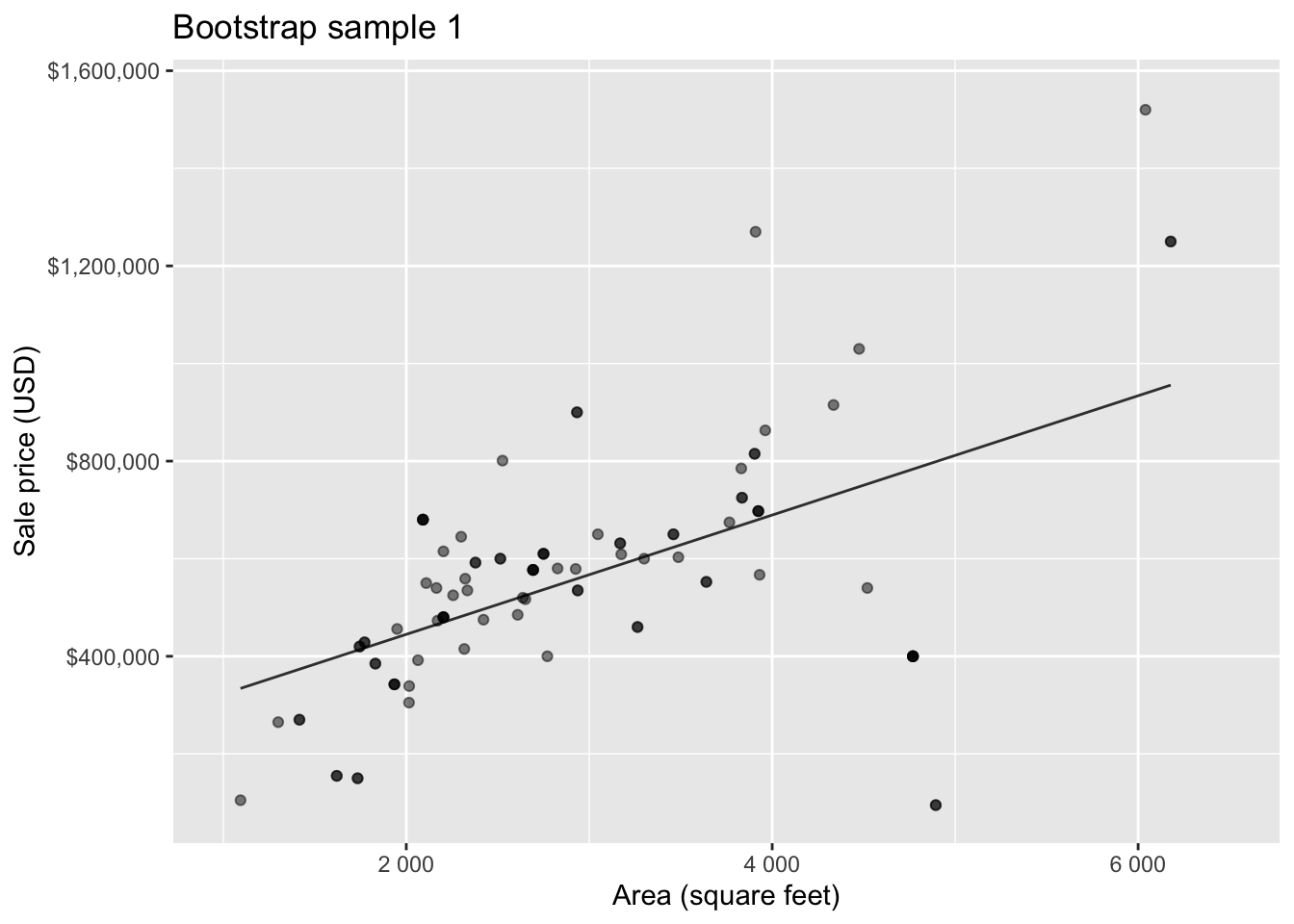
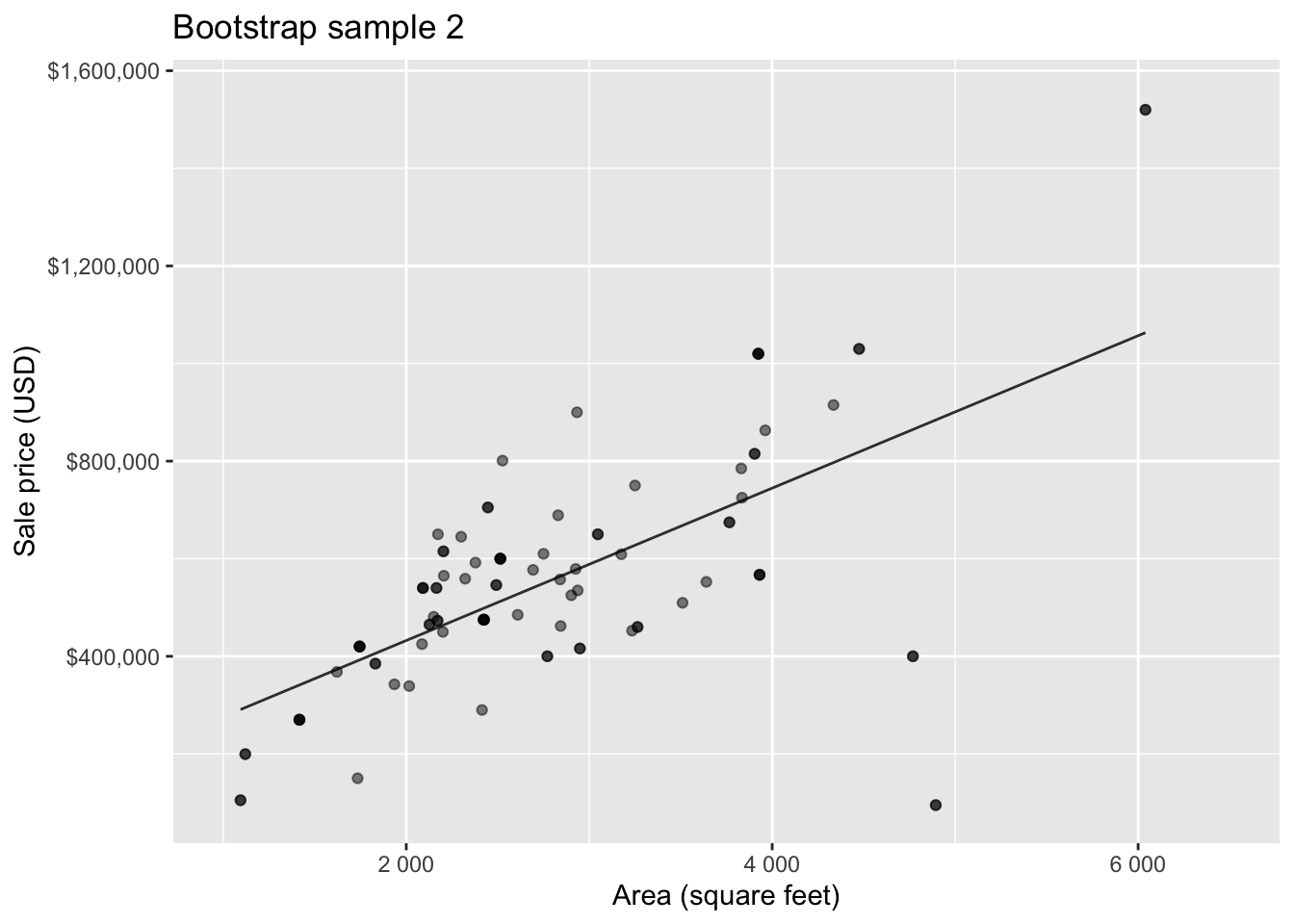
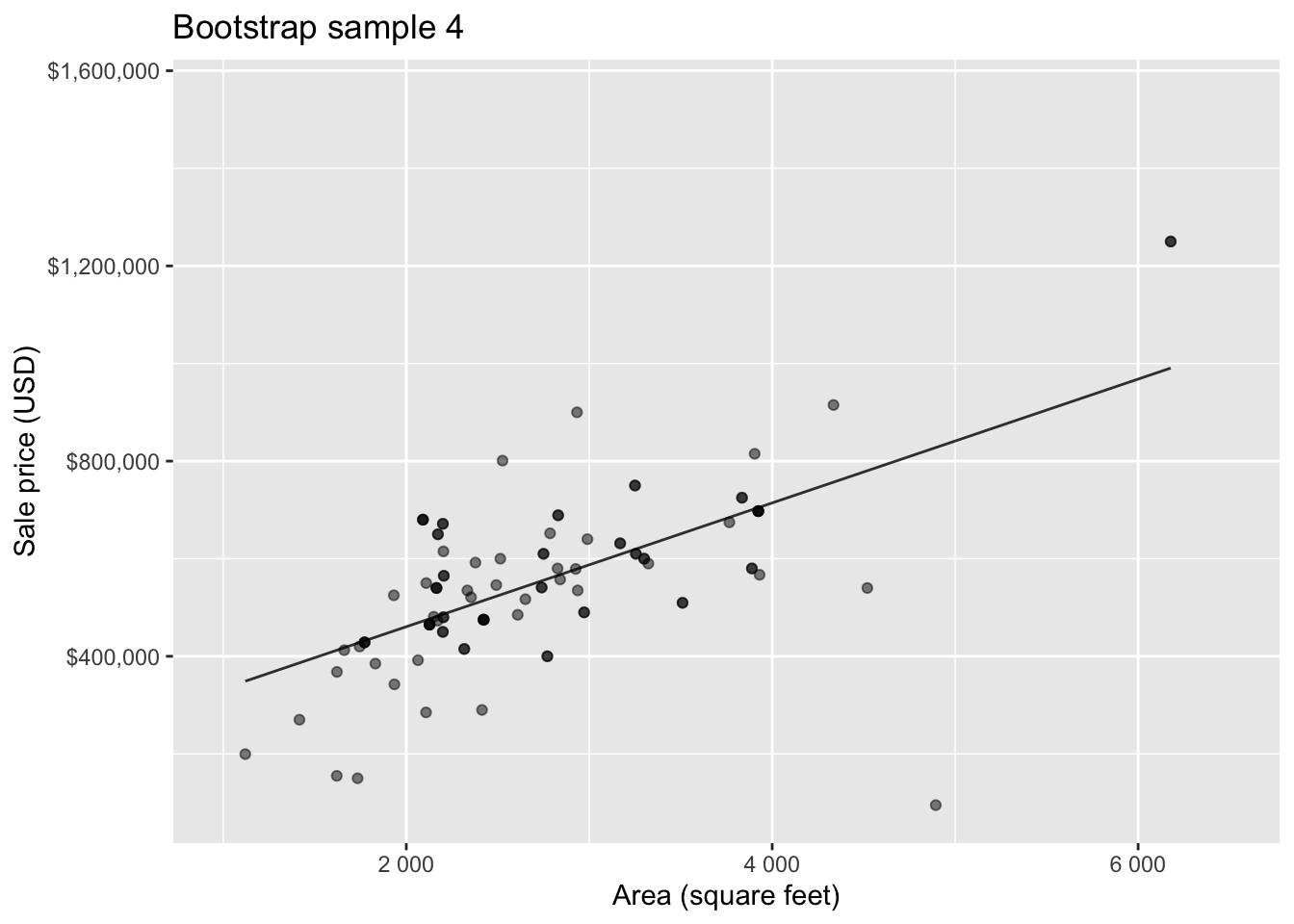
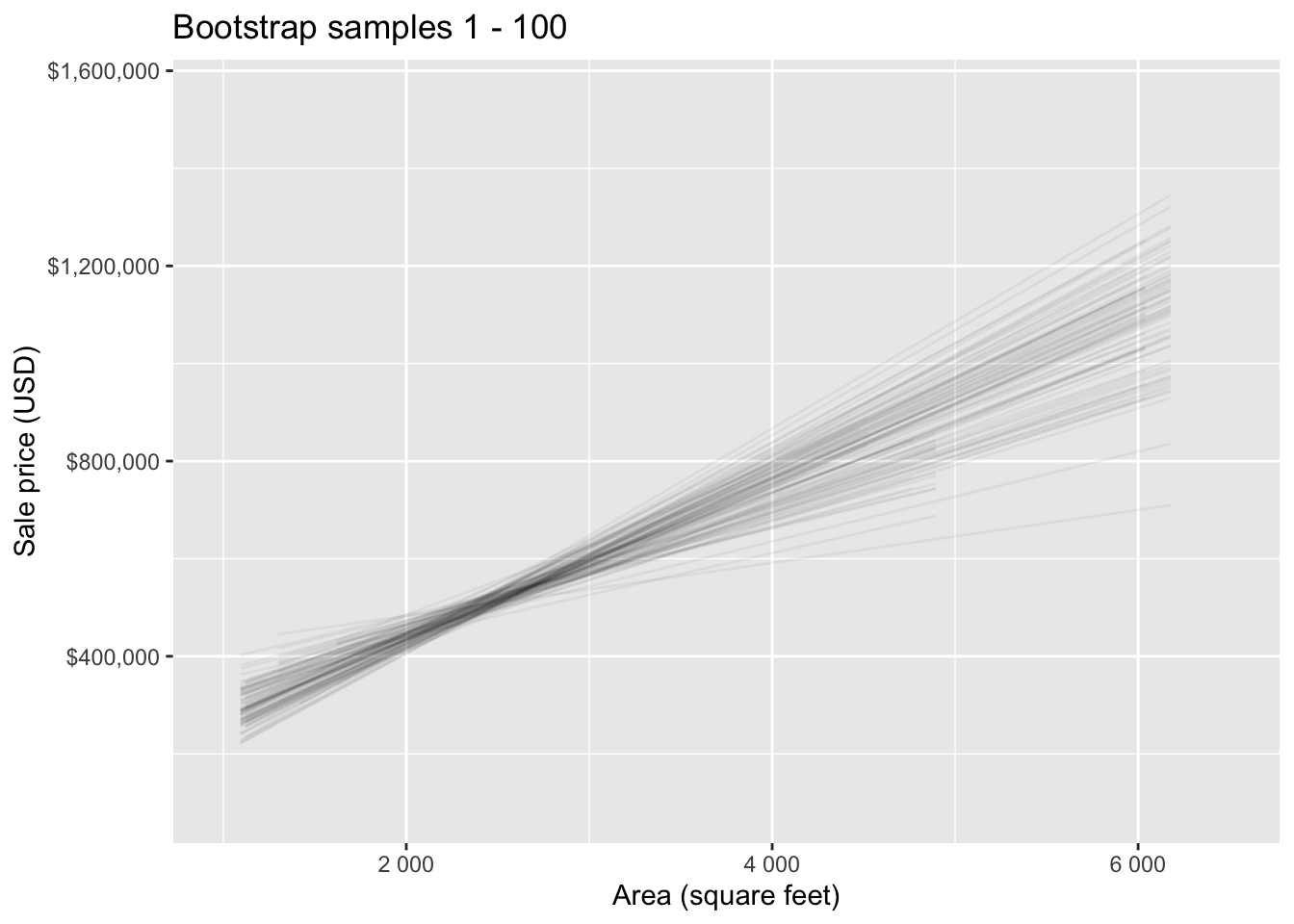
Bootstrapping to quantify the variability of the slope for the purpose of estimation:

• Bootstrap new samples from the original sample
• Fit models to each of the samples and estimate the slope
• Use features of the distribution of the bootstrapped slopes to construct a confidence interval

Bootstrap sample 1

Bootstrap sample 2

Bootstrap sample 3

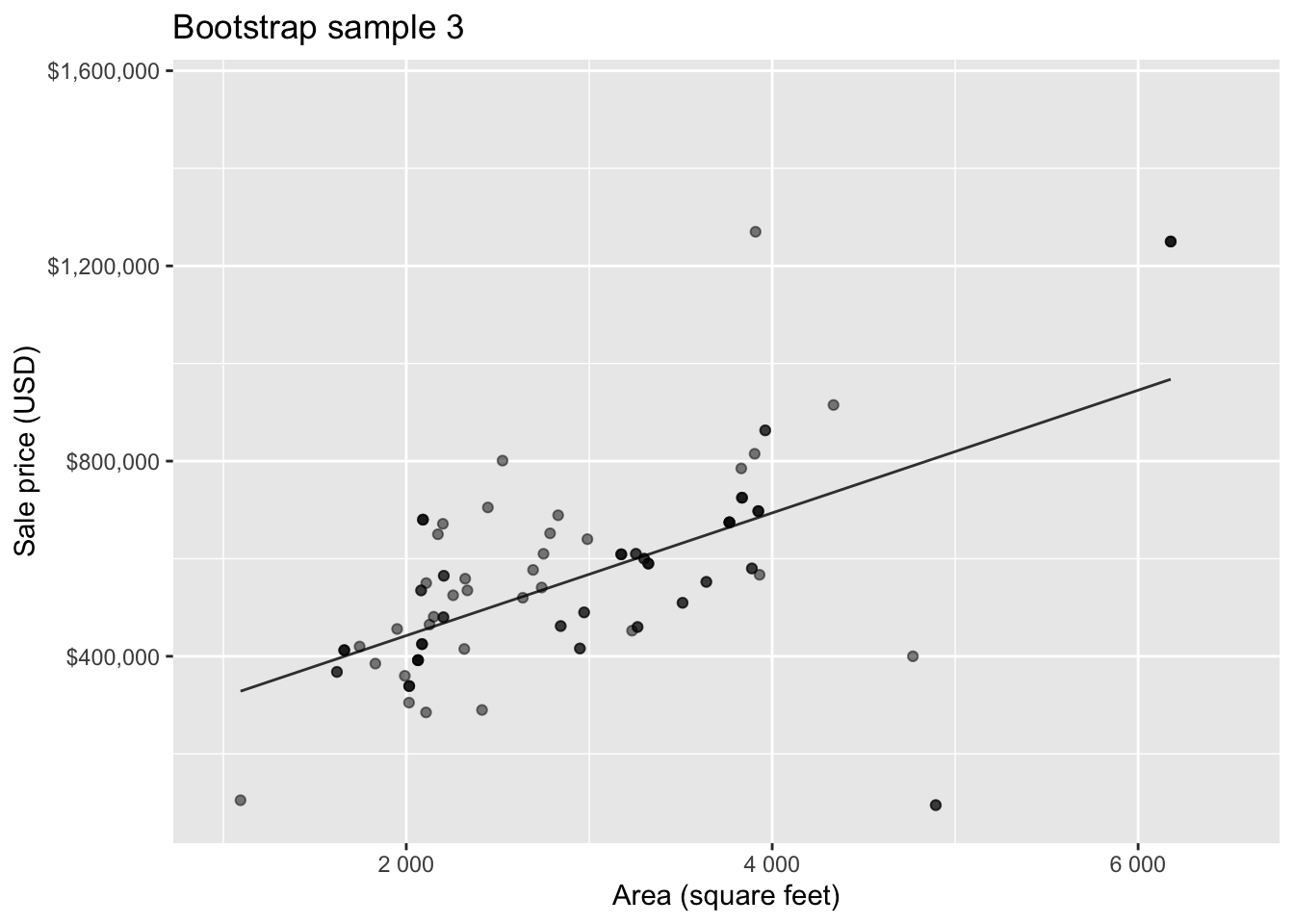
Bootstrap sample 4

Bootstrap sample 5

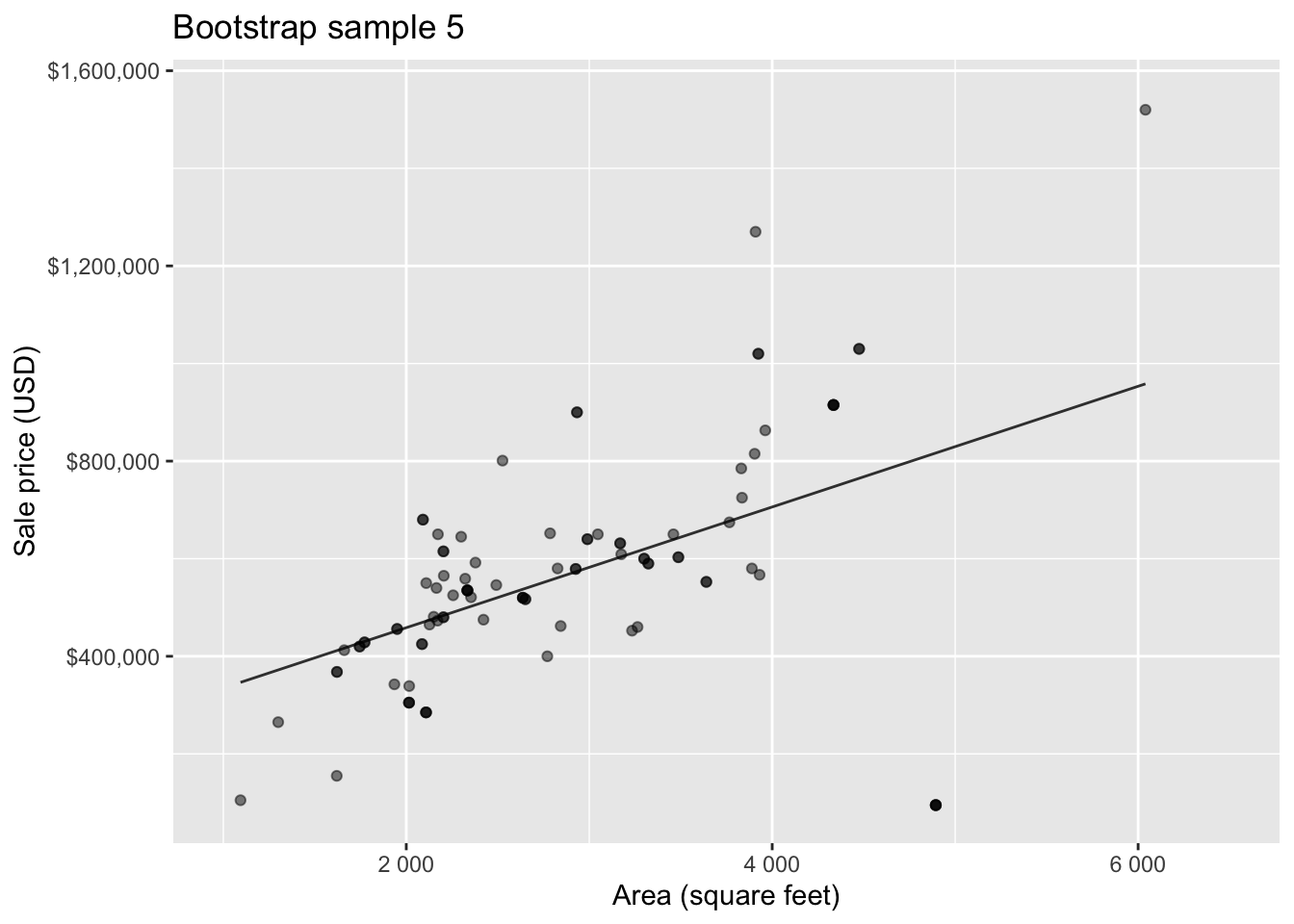
so on and so forth…

Bootstrap samples 1 - 5

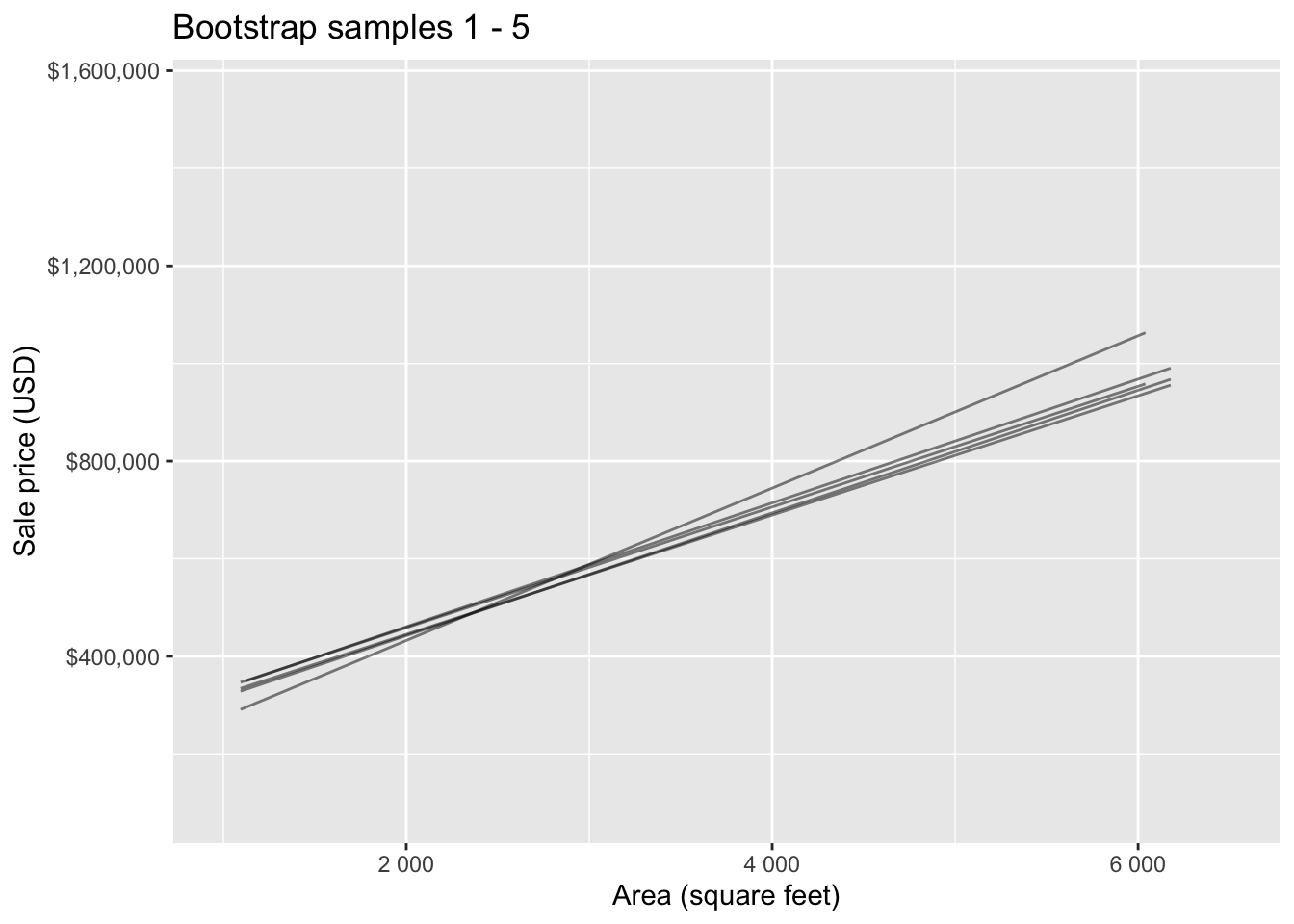
Bootstrap samples 1 - 100

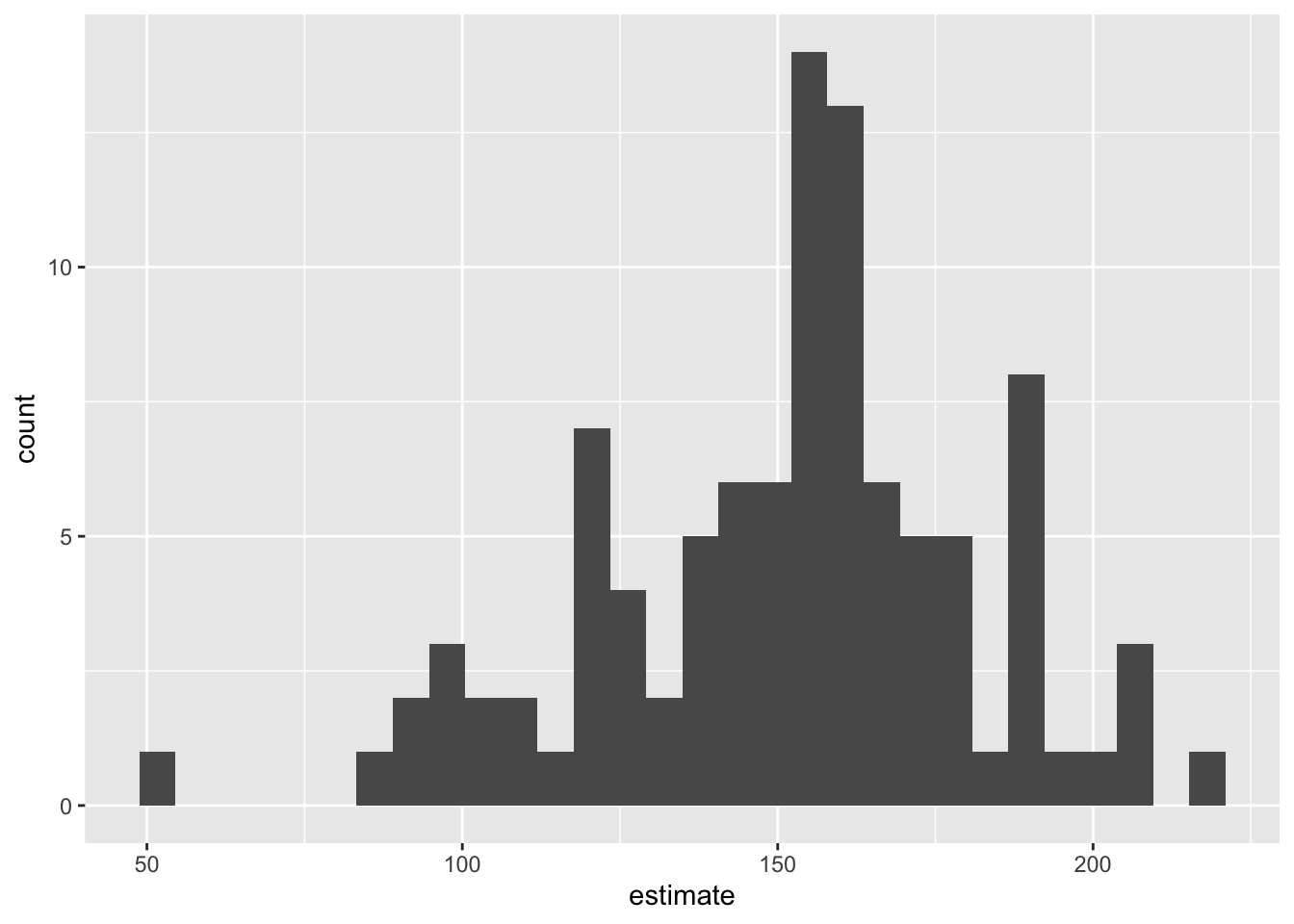
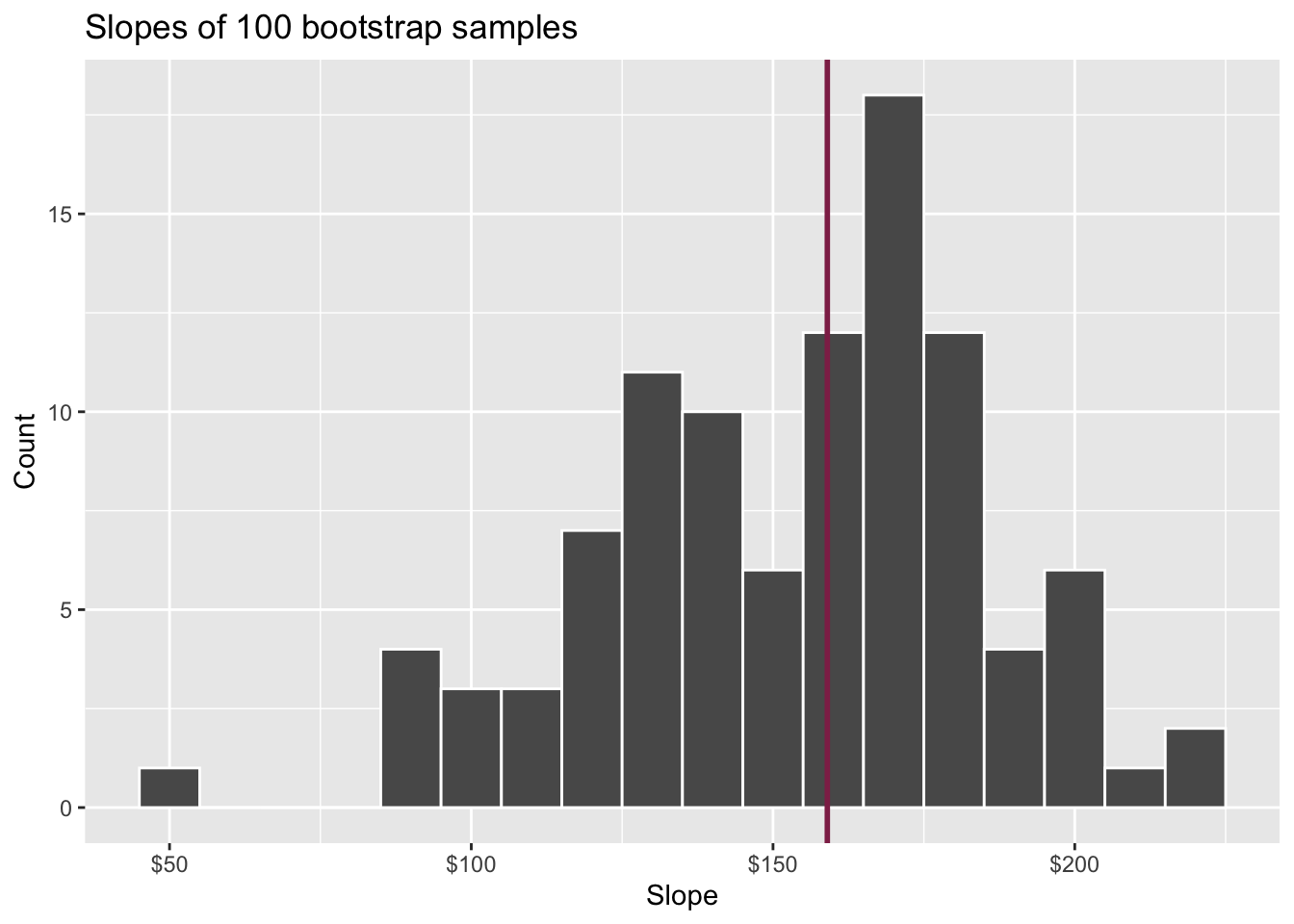
Slopes of bootstrap samples

Fill in the blank: For each additional square foot, the model predicts the sale price of Duke Forest houses to be higher, on average, by $159, plus or minus ___ dollars.

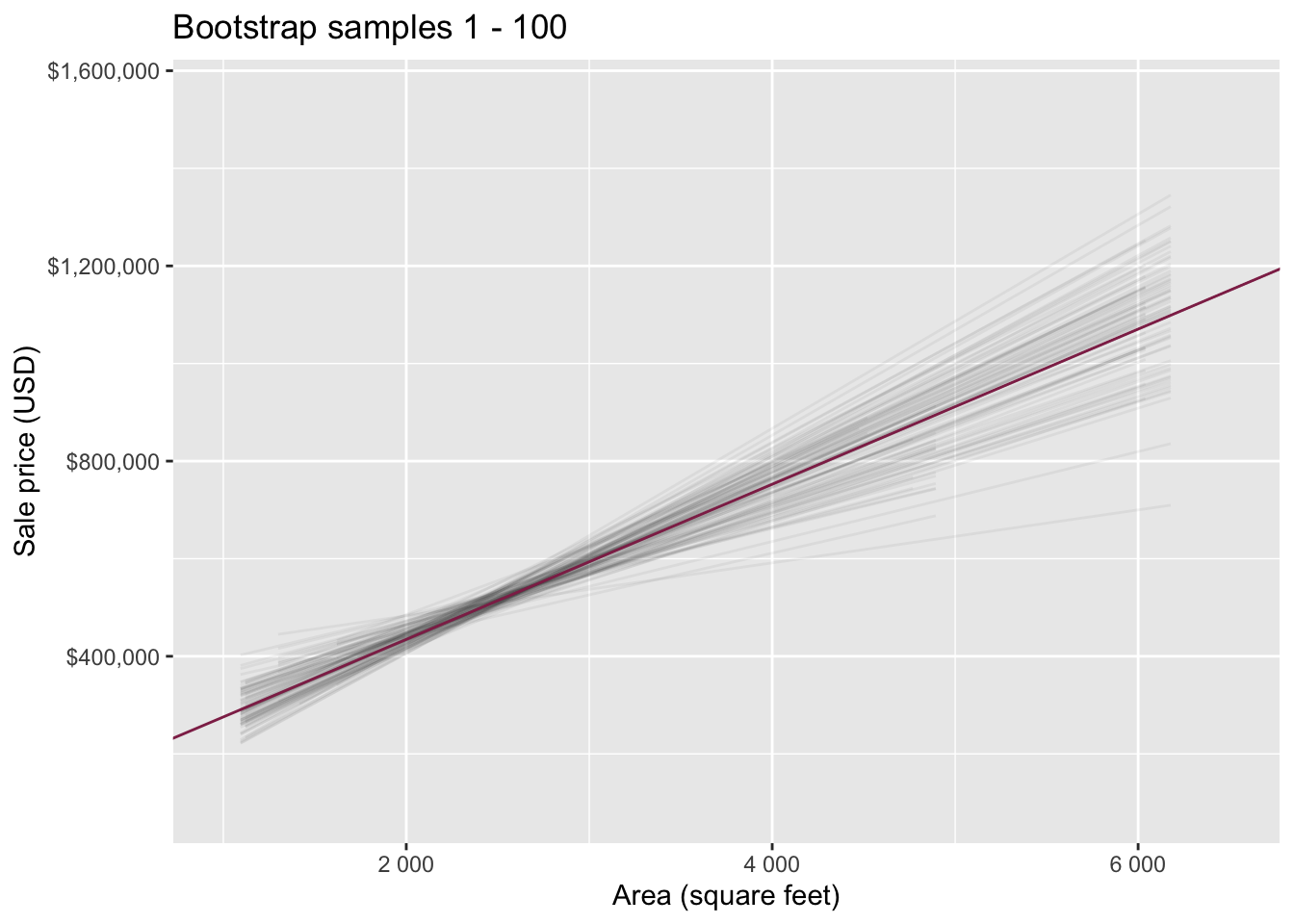
Slopes of bootstrap samples

Fill in the blank: For each additional square foot, we expect the sale price of Duke Forest houses to be higher, on average, by $159, plus or minus ___ dollars.

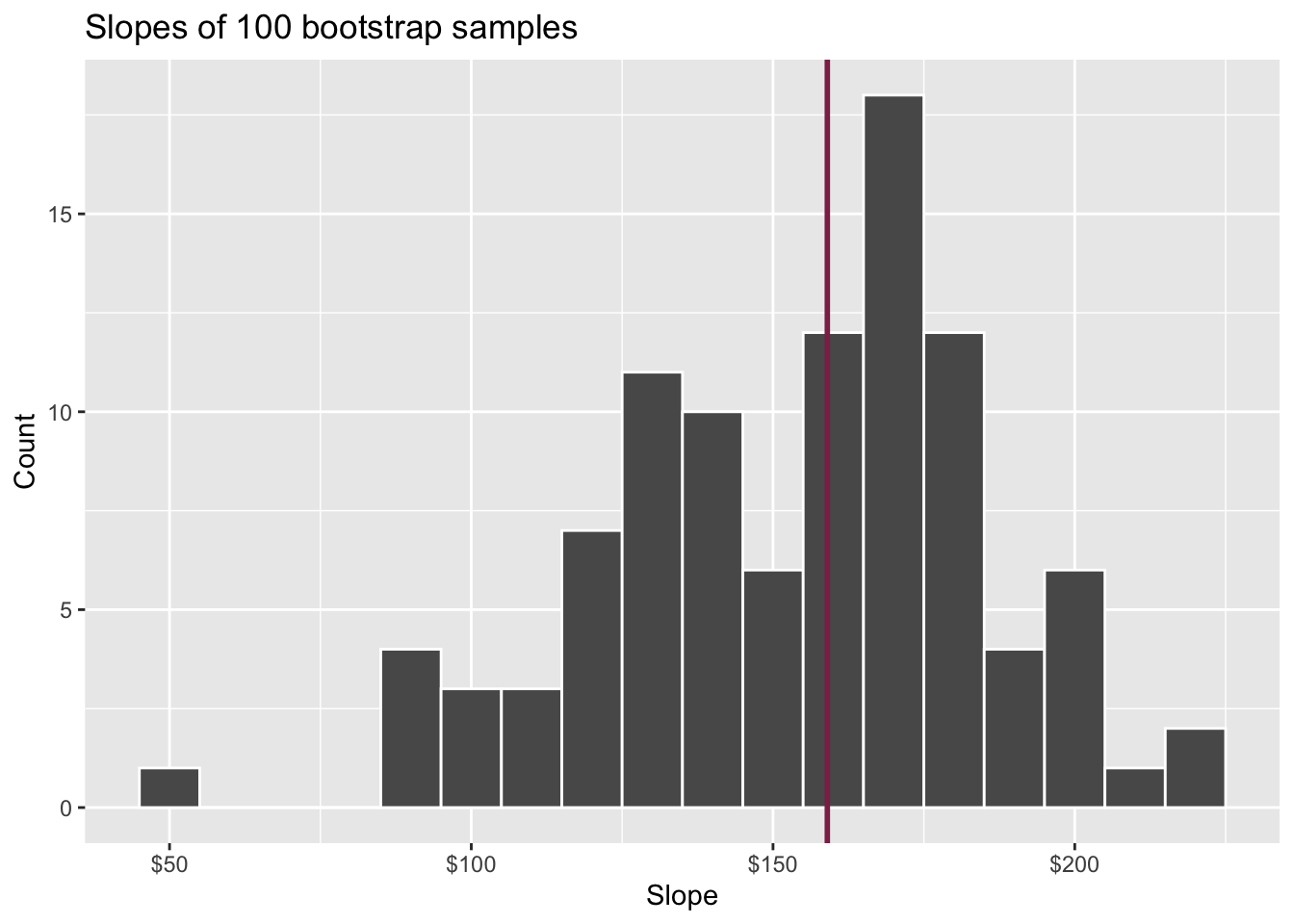
Confidence level

How confident are you that the true slope is between $0 and $250? How about $150 and $170? How about $90 and $210?

95% confidence interval

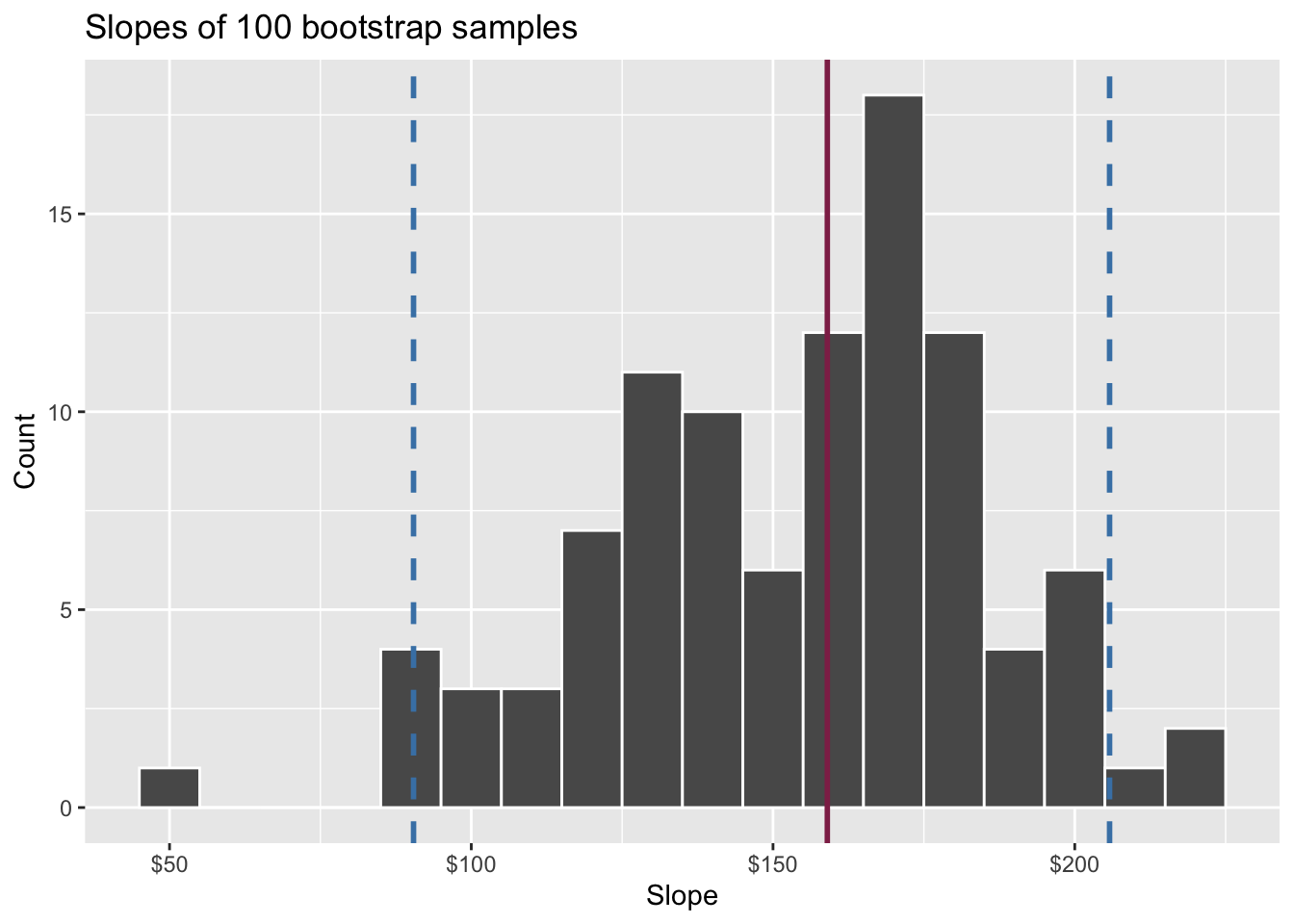
• A 95% confidence interval is bounded by the middle 95% of the bootstrap distribution
• We are 95% confident that for each additional square foot, the model predicts the sale price of Duke Forest houses to be higher, on average, by $90.43 to $205.77.

Application exercise

Calculate observed fit

Calculate the observed slope:

observed_fit <- duke_forest |>
  specify(price ~ area) |>
  fit()

observed_fit

# A tibble: 2 × 2
  term      estimate
  <chr>        <dbl>
1 intercept  116652.
2 area          159.

Take bootstrap samples

Take 100 bootstrap samples and fit models to each one:

set.seed(1234)
n = 100

boot_fits <- duke_forest |>
  specify(price ~ area) |>
  generate(reps = n, type = "bootstrap") |>
  fit()

boot_fits

# A tibble: 200 × 3
# Groups:   replicate [100]
   replicate term      estimate
       <int> <chr>        <dbl>
 1         1 intercept  177388.
 2         1 area          125.
 3         2 intercept  161078.
 4         2 area          150.
 5         3 intercept  202354.
 6         3 area          118.
 7         4 intercept  120750.
 8         4 area          162.
 9         5 intercept   52127.
10         5 area          180.
# ℹ 190 more rows

Examine bootstrap samples

boot_fits |>
  filter(term == "area") |>
  ggplot(aes(x = estimate)) +
  geom_histogram()

Computing the CI for the slope III

Percentile method: Compute the 95% CI as the middle 95% of the bootstrap distribution:

get_confidence_interval(
  boot_fits, 
  point_estimate = observed_fit, 
  level = 0.95,
  type = "percentile" 
)

# A tibble: 2 × 3
  term      lower_ci upper_ci
  <chr>        <dbl>    <dbl>
1 area          92.4     206.
2 intercept   7014.   285255.

Precision vs. accuracy

If we want to be very certain that we capture the population parameter, should we use a wider or a narrower interval? What drawbacks are associated with using a wider interval?

Precision vs. accuracy

How can we get best of both worlds – high precision and high accuracy?

Changing confidence level

How would you modify the following code to calculate a 90% confidence interval? How would you modify it for a 99% confidence interval?

get_confidence_interval(
  boot_fits, 
  point_estimate = observed_fit, 
  level = 0.95,
  type = "percentile"
)

# A tibble: 2 × 3
  term      lower_ci upper_ci
  <chr>        <dbl>    <dbl>
1 area          92.4     206.
2 intercept   7014.   285255.

Changing confidence level

## confidence level: 90%
get_confidence_interval(
  boot_fits, point_estimate = observed_fit, 
  level = 0.90, type = "percentile"
)

# A tibble: 2 × 3
  term      lower_ci upper_ci
  <chr>        <dbl>    <dbl>
1 area          96.1     197.
2 intercept  20626.   268049.

## confidence level: 99%
get_confidence_interval(
  boot_fits, point_estimate = observed_fit, 
  level = 0.99, type = "percentile"
)

# A tibble: 2 × 3
  term      lower_ci upper_ci
  <chr>        <dbl>    <dbl>
1 area          69.7     214.
2 intercept -25879.   351614.

Recap

• Population: Complete set of observations of whatever we are studying, e.g., people, tweets, photographs, etc. (population size = \(N\))

• Sample: Subset of the population, ideally random and representative (sample size = \(n\))

• Sample statistic \(\ne\) population parameter, but if the sample is good, it can be a good estimate

• Statistical inference: Discipline that concerns itself with extracting meaning and information from data that has been generated by random process

• We report the estimate with a confidence interval. The width of this interval depends on the variability of sample statistics from different samples from the population

• Since we can’t continue sampling from the population, we bootstrap from the one sample we have to estimate sampling variability

  linear_reg() |>
    fit(wt ~ cyl + hp, data = mtcars)

parsnip model object


Call:
stats::lm(formula = wt ~ cyl + hp, data = data)

Coefficients:
(Intercept)          cyl           hp  
  0.5820880    0.4177733    0.0003422